普遍联系

 

万事万物是普遍联系的，这种观点并不新奇，然而令人意想不到的是这一哲学观点正在引发一场从微观到宏观的科学范式转变。更令人意想不到的是，我们正在举行的凯风－集智研读营——一个仅仅由16个年轻学者参与的为期5天的小型研讨会——正在见证这一变革。

 

我的眼前不禁又浮现出尤亦庄在讲台上的奕奕神采。这个总是低头沉思的大男孩在讲起物理的时候就仿佛换了一个人，声音高亢而洪亮。更有意思的是他讲的内容。

 

 

用著名物理学家文小刚的话说，现在的理论物理学正在经历一场革命，这场革命不但有望统一相对论和量子力学，更有可能统一微观与宏观、物质与信息。而这一革命背后，正是从面向对象的物理学到面向关系的物理学的范式转变。在新的图景下，我们的宇宙是一台大型的量子计算机。生命、智能、人类社会都不过是这台大型计算机上涌现出来的Pattern。

 

一切都要从量子纠缠说起。所谓的量子纠缠是指两个量子比特存在着的一种很强的联系，在这种联系下它们仿佛就是一个整体，甚至这两个比特已然相隔万里。这就是让大科学家爱因斯坦也唏嘘不已、不愿意接受的量子纠缠：两个明明分离的部分却表现得像一个整体。

 

正是因为量子纠缠的存在，量子体系可以拥有比经典系统更强的信息存储能力，因为信息不仅可以存储在独立的量子比特中，还可以存储在两个比特的纠缠——即关系之中。而且，纠缠存储的信息是两个比特，足足比经典的相关性增加了一比特的存储量。

 

  “我就不明白，量子纠缠与经典的相关性究竟有什么联系？”，吴令飞一边嚓嚓地踩着落叶一边问道，“比如，我有一对手套，我把其中的一支送到月球上，当我看到我自己手中的手套是左手的时候，我自然可以推知月球上的手套必然是右手，这不是也是一种纠缠吗？”

 

“嗯，这个问题的确问得好……”我一边沉思着一边回忆着尤亦庄给出的解释，复述给吴令飞，“然而，在手套这个例子中，当你得知了手套的左右属性后，你就不能在这二者的联系中获得更多信息了。而假设手套是量子的，你不仅可以从一支量子手套的测量中获得另一支手套是右手的信息，你还可以测量手套的第二个属性，从而获得额外的一比特的信息。也就是说，量子的两比特纠缠会比经典的两比特相关包含更多的信息，这恰恰是贝尔不等式所推导出的内容。”

 

“物理学家都是外星人吗？”，当尤亦庄讲到我们可以用张量网络来表示量子纠缠的时候，苑明理脱口而出这句话。的确，张量网络不仅可以巧妙地用网络图形表示复杂的高阶张量计算，而且可以简单轻松地表达处于复杂纠缠的量子体系。如下图：

 

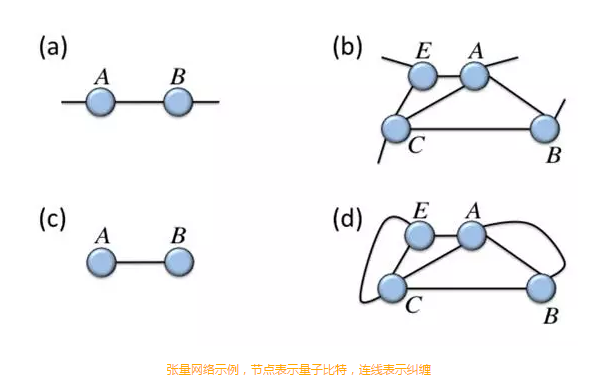
网络中的节点都是量子比特，连边就表示这两个量子比特之间的纠缠，连边的权重表示了纠缠熵。有了这种工具，我们就可以轻而易举地研究多体之间的纠缠关系，还可以进行复杂的张量计算。

 

一个量子系统的演化完全可以用这个网络的演化来表示。有意思的是张量网络的演化会服从一些类似社会网络中的规则：链接具有一定的传递性，即如果A和B相连，且B和C相连，那么A就很可能会与C相连。有了这种传递性，一个网络在演化的过程中就会更容易地形成长程连接。所以当我们制备了一个量子体系，那么由于它与环境的退相干（de-coherence）作用，它就会与环境建立越来越多的链接。

 

既然信息都存储在了这些纠缠之中，那么一个体系的熵就可以形象地表现为该系统与外界发生的联系数量（也就是张量网络中的连边）。所以，当我们想知道某一个系统（张量网络中的一个子区域）的熵的时候，我们只需要知道当我们把该系统完全清晰地划分出来，所需要切断它与外界的连边总权重之和。

 

于是，结合前面两点，我们就能得出热力学第二定律。我们知道，热力学第二定律可以表述为：任何一个孤立系统的演化都趋于熵增，也就是存在着一个时间箭头，它的指向为熵增。而与其矛盾的是，微观世界的物理学（无论是牛顿经典力学还是量子力学）中的演化都是时间反演对称的，即不存在时间箭头。那么，我们观察到的熵增现象是怎么回事儿呢？

 

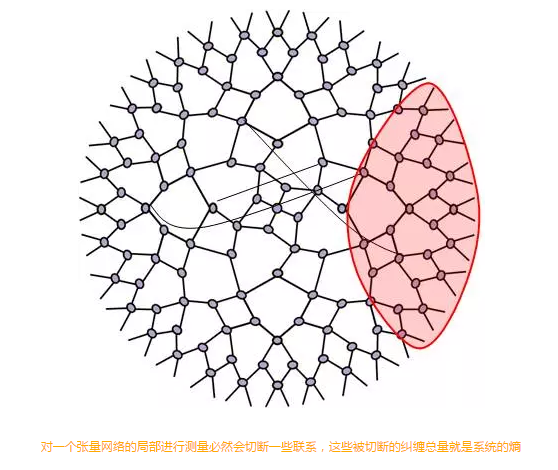
人们曾试图从牛顿经典力学推导出热力学第二定律，但都没有成功。而最近几年的物理学进展却使得我们可以从量子纠缠的角度重新推导热力学第二定律。一方面，任何一个量子体系的纠缠都在逐渐趋向于长程弱联系；另一方面，我们每一次测量都只能测量到整个系统中的一小部分，于是，我们就不得不割裂这一小部分与系统外界的量子纠缠。而我们知道，这些被割裂边的权重之和就是被测量体系的熵。所以，我们就会得到熵会不断增加的结论。

 

让我们换一种表述方法，其实所谓的熵增并不存在。因为，当系统按照量子力学薛定谔方程的模式进行演化的时候，系统会建立越来越多的长程联结，即系统的每一个局部的信息都会弥散在整个系统之中。而我们人类无法对整个系统（宇宙）进行测量，而只能测量到系统之中的一小部分，于是，我们就无法还原弥散在整个系统之中的信息，而得到熵不断增加的结论。

 

小镇里面的游人开始渐渐多了起来，一些游客与我擦肩而过，时不时还会发生一些身体上的接触。“他们在带走我身上的信息”，我突然冒出了这样一个念头。可不是吗，假如我是一个量子比特，我与这些人的每一次碰撞实际上就是一起纠缠事件，而每一次纠缠都会使得我身上的信息被不断分散在整个人群之中。假如我想让我某一天的生活重新来过，我只需要将与我相互作用过的每一个人集合起来，收集我身上的信息，原则上讲就能够让时间停止甚至逆转。

 

我突然想起了前段时间听到过的一个MIT学生的非常有创意的项目构思：利用机器学习技术，我们也许可以通过地面上的一张小纸片的微小震动模式来推断房间中人们发声所说出来的语言是什么，也许未来不需要窃听器就可以盗取信息，因为这些信息实际上都分布到了环境的每一个角落。 

 

双曲几何

 

当然，量子纠缠、张量网络这一套东西的威力还不仅如此，除了导出热力学第二定律外，它还能推出更多激动人心的东西。

 

在物理中，有两个东西比较相似，一个是量子纠缠，一个是虫洞。这两种东西都具有非局域特性，同时，也都非常不稳定。

 

所谓的虫洞，是一种时空结构，可以直接从爱因斯坦的广义相对论中得到。这种结构可以通过空间中的特殊通道，将两个原本相隔非常远的空间重新联通到一起。不过，这种结构是非常不稳定的，它的寿命也极其短暂。

 

再来看量子纠缠，它也具有非局域特性，而且也是极其不稳定的。为了避免退相干，人们需要精心制备实验条件，这也是为什么量子计算机制造极其困难的原因。我们很难长时间维持一个长程的纠缠。

 

正是由于量子纠缠和虫洞之间的相似性，这使得人们大胆猜测，量子纠缠实际上就是虫洞。当两个相隔很远的量子比特处于相互纠缠状态的时候，它们彼此之间实际上有着空间中的虫洞相连。

 

于是一个存在长程关联的无引力的共形场可以等价于一个局域的量子引力场，这就是物理上著名的AdS/CFT对应。因为长程关联（纠缠）系统中的纠缠全部对应为了超空间连接的虫洞，于是，在新的AdS空间中增加了很多新的联系，这些联系就使得新空间成为一种双曲空间。如果我们将长程关联的共形场看作一个圆环，那么对应的引力场就是一个彭加来原盘（双曲空间的一个模型），如下图所示：

 

如上图所示，这是AdS/CFT变换的示意图，边界上存在着一个没有引力的但是处于临界状态的相互关联的共形场，而边界内部则是一个双曲空间（AdS空间）。于是，在新的空间中，长程的相互联系消失了，空间成为了双曲的。

 

从数学上说，双曲空间就是曲率为负的空间。它实际上可以看成是树这种结构的离散版本。在这种空间中，空间的度规会随着距离的增大而呈指数增长。

 

这种AdS/CFT对应不仅能够让我们看到引力理论和处于临界状态的长程关联系统之间的联系，而且还能够帮助我们找到理解普遍存在的临界现象的方式，即双曲空间。所谓的临界现象是指系统在一定条件下所展现出来的一系列无标度效应，例如系统的各个变量呈现幂律分布和幂律相关，系统存在着尺度对称性（即分形特性）。最重要的是，临界系统都存在着长程关联，即关联强度随着尺度呈现幂律方式的衰减。

 

由于临界系统中的长程关联，所以经过这种变换，在双曲空间中，我们就可以将这些长程关联消除掉。然而，它的代价就是增加了一个新的维度，即系统的标度。于是，沿着双曲空间Poincare圆盘的半径方向，我们可以对边界上的临界系统做持续不断的重整化操作。

 

复杂网络

 

如果说一个认识仅仅对理论物理问题有启发，那么我对它的兴趣就不会很大，因为我毕竟不是搞物理的。然而，体－边界对偶这套东西恰恰可以应用到复杂系统之中。认识到这一点，还要从三年前的一次集智活动谈起。

 

时间回到了2013年的一个夏天，集智照常举办公开活动。这次，是我自己主讲，内容是复杂网络。当时，尤亦庄还是清华大学高等研究院的博士生，对复杂网络正兴趣十足。我大致列举了近些年来复杂网络发展的几个关键文章，其中讲到了一个希腊小伙Fragkiskos Papadopoulos做的工作，他提出了一个在双曲空间上生长的网络模型，如下图所示：

 

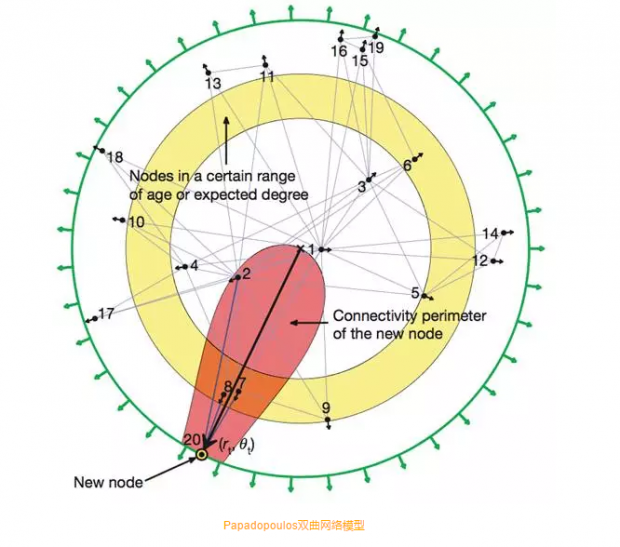
如图，这是一个在双曲空间Poincare圆盘模型上生长的网络。其中，每一个节点（对应着1，2，3……这样的编号）都有两个坐标，一个是它的极径（到中心点的距离），另一个是它的极角，每一个节点都按照双曲空间中距离最近的方式进行连接。

 

每当一个新节点诞生的时候，它的极径就被设定为ln t，其中t就是当前时刻，而它的极角可以随机地从0到2π之间选定一个数值。每一个新节点诞生都会带来m条新的连边（m是一个参数），这些连边就将这个新节点连接到离它最近的m个近邻上。注意，这里面的距离是双曲空间中的距离。在图中，红色的类似于舌头一样的区域就是一个以新节点20为中心的双曲圆，即区域中的点到20节点的双曲距离都是相等的。也就是说，空间在径向和圆周方向并不对称。于是，新节点会连接更老的节点（ln t更小），或者是极角和自己更相近的节点。

 

该模型将这两个坐标赋予了实际含义：极径表示的是节点的流行度，越老的节点就越流行——因为它们可以竞争得到更多的连接。而极角则被解释为流行性，即在极角方向上越靠近的节点，它们彼此越相似。所以，一个新点进入系统后，要么连接那些很有威望的老节点，要么连接和自己相似的节点。流行性和相似度构成了一对竞争。

 

最有意思的是，该模型可以复现出著名的优先连接模型（Preferential attachment），也能够得到小世界的特性。而且，这个模型的各种变种几乎可以复现所有已知的复杂网络模型。

 

然而，在三年前的那次讲座中，我自己却没有认识到这个模型的重要性，以为这些都只不过是酷炫的数学以及一些奇技淫巧。其实，之所以这样认识，完全是因为我当时对所谓的双曲几何这种概念非常陌生。

 

“这不就是Anti de Sitter空间吗？”坐在台下听讲座的尤亦庄马上兴奋了起来，他兴致高昂地说道，“原来复杂网络学者们已经走到了前面！”

 

会后，我们就对双曲几何进行了更深入地探讨。原来，我们在很多复杂系统中看到的那些诸如标度律、幂律分布、分形几何等临界现象，都可能暗示着它的背后存在着双曲几何。然而，由于时间仓促，我对这些高深的理论物理知识仍然一知半解。

 

时间拉回了今天，当我听过了尤亦庄的精彩讲座之后，终于对什么是张量网络有了比较全面的了解，也对尤亦庄当时所说的临界系统与双曲几何的关系有了更深刻的认识。

 

在很多复杂系统中，层级现象都非常地普遍。如果我们将层级作为一种新的维度（也就是双曲几何中的径向维度），那么我们就可以将复杂系统按照层级进行展开，这样，每一层就构成了一个尺度的相似性空间。而复杂系统之所以会展现出各种各样的临界现象，恰恰是因为它背后存在着双曲几何机制。于是，经过体－边界对偶关系，利用新的层级维度，我们就可以将普遍存在的长程相互作用化简为局域的相互作用。

 

然而这种奇怪的双曲几何真的存在于我们身边的复杂系统吗？我们怎么没有体会到弯曲的时空呢？

 

有意思的，董磊的报告让我们看到，由于现代城市中的疏运交通网络的作用，我们的空间已经被弯曲变形了，最终的形状真的有可能具有一种双曲结构。如下图所示：

 

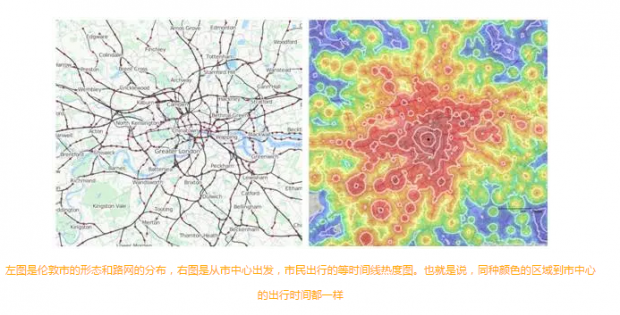
左图是伦敦市的形态和路网的分布，右图是从市中心出发，市民出行的等时间线热度图。也就是说，同种颜色的区域到市中心的出行时间都一样

 

于是，假如我们根据等时线来重新定义度规，就会得到扭曲变形后的城市地图。这种方法可以很好地展现出城市交通的自然演化对空间扭曲程度的影响。

 

机器学习

 

然而，尽管这套理论可以自圆其说，而且似乎能让我们看到它和理论物理的深刻联系，但是，它究竟如何指导我们的实践呢？这恐怕离不开机器学习技术！

 

当下，机器学习大火。越来越多的机器学习、深度学习技术被用来解决人们日常生活中的问题。其中，网络嵌入（network embedding）就与我们讨论的几何与网络的主题紧密相关。

 

这还要从诞生于2013年的一项自然语言处理技术Word2Vec说起。Word2Vec是一套将单词嵌入到高维空间中的技术，通过训练一个神经网络，得到每个单词的向量。每个单词的向量和它所出现的上下文单词有关，相似的单词会出现在相似的地方。

 

更令人惊奇的是，这种技术不仅仅能够精确地计算单词之间的相似性，还能够得到单词之间的抽象关系。例如，一个著名的公式是：v(男人)-v(国王) ≈ v(女人)-v(王后)。

 

其中v(x)表示x这个单词的词向量。也就是说，机器会自己学习到男人相对于国王相当于女人相对于王后。所以，除了将每个单词进行了向量表示以外，Word2Vec还可以隐式地学习到“最高权力”这种关系。

 

后来，有人将这套东西用到了复杂网络上。为什么自然语言处理的技术能够用到复杂网络上呢？原来，网络上有个东西叫做随机游走。即我们可以放一个随机游走的粒子到网络上，然后让它沿着网络的连边随机的跳转，这样这个粒子就可以走出来一个节点的序列，例如：3→1→2→5→7→….我们便可以将这样一个序列看作一句话，每一个节点的编号看作是一个单词。于是，我们便可以将大量这样的粒子随机游走出来的节点序列扔给Word2Vec做训练，就得到了每一个节点的向量表示。这就叫网络嵌入，即将每个节点嵌入到了一个高维的空间中。于是，我们利用机器学习的方式，建立了一种网络和几何之间的关系。这一套算法叫做DeepWalk，它可以很好地表示网络，并且，相似的节点（处于相同社区的节点）都会被聚集在一起。有大量的网络嵌入算法被总结成了流行学习这样一个分支（吴令飞在研读营中做了专门的介绍）。

 

然而，这种方法也不是十全十美，其中一个最大的问题就是它无法区分不同层次的节点。比如，在自然语言中，“The, a”这种单词经常出现，于是它们也会被嵌入到整个网络所有节点的中心位置。然而，我们明显地知道这种单词是与其它的单词不同的。同样地，在复杂网络中，有一些核心节点仅仅是因为处在了Hub的位置才与所有的节点都相连，而实际上它们并不与其它的节点相似。但是，DeepWalk算法却并不能区分这种位于高层次的节点。

 

因此，我们应该将双曲几何模型中的流行性考虑到机器学习算法过程中。也许，我们通过将这种层次性的因素过滤掉之后，就可以更好地将同层次的节点嵌入到合适的向量空间中，而且在这样做的过程中，我们或许可以自然地得到网络相似性空间的维度。

 

目前所有的网络嵌入算法都是将维度作为一个外生变量引入的，我们并不能先验地确定一个具体的空间维数。但是，如果我们将节点的层次性因素去掉之后，不断提升嵌入空间的维度，就有可能得到误差曲线的一个相变，于是这个临界的维度值就应该是网络本身特征空间的维度值。

 

统计物理

 

这个时候，张潘在白板上推导公式的场景再一次浮现在我的眼前。他从一个统计物理学家的特殊视角统一了几大类计算问题。在他看来，所谓的极大似然估计和贝叶斯统计推断不过是统计物理系统在不同温度谱系上的特例。当我们将温度这个阀门调节到0的时候，我们就得到了极大似然估计方法；而当我们将温度调节到1的时候，就得到了贝叶斯统计推断。物理学家强大的地方就在于，一旦他们看懂了一个问题，他们就能一下子把握住该问题的本质并作出推广。

 

具体来讲，很多计算问题的求解都存在着相变。比如，对于图的染色问题，不同的网络对应着不同的难度。于是，我们便可以利用ISING模型来对这类组合优化问题进行建模，从而将统计物理学家发明的各类巧妙的近似方法（例如cavity方法）应用其中。

 

我猜，网络的空间嵌入也存在着类似的相变。为了求得每个节点在表示空间中的位置，我们就要去优化节点的位置变量，让它们的总误差最小。这很像ISING模型（严格说，应该是POTTS模型），其中节点是自旋，误差是能量；也许维度D就是一个序参量，对它的调节会导致相变。于是，物理学家发明的一大套高明的技巧就可以被用来分析这一现象。

 

于是，我们看到了一条统一的道路：从量子纠缠到复杂网络，再到双曲空间、机器学习和统计物理。当我看清了整个道路，就有了一种打通了七经八脉的感觉。也许，跨学科交叉的意义就在于此，它能让你看到不同学科之间的深刻联系。

结语

五天时间一晃而去，尽管我们是在紧张的讨论和学习中度过的，但是每一个人都对此次研读营留下了深刻的印象。在最后的总结晚宴过程中，每一个人都表达了这次活动的效果远远超出预期的感受。

 

再见了，集智－凯风研读营；再见了古北水镇；再见了，令人尊敬的学者们；再见了，亲爱的朋友们。

 

张江

 

于2016年10月

 

参考资料

 

[1] 尤亦庄关于本次研读营课程的讲义：

http://wiki.swarma.net/index.php/2016%E7%A0%94%E8%AF%BB%E8%90%A5%E4%B9%8B%E5%BC%A0%E9%87%8F%E7%BD%91%E7%BB%9C

 

[2] 关于量子信息与量子计算：Michael Nielson &Issac L.Chuang, Quantum computation and quantum information, Cambridge University Press,2001

 

[3] 关于张量网络：https://arxiv.org/pdf/1106.1082v1.pdf

 

[4] 复杂网络的双曲模型：Papadopoulos F, Kitsak M, Serrano MÁ, et al. Popularity versus similarity in growing networks[J]. Nature, 2012,489(7417): 537-540.

 

[5] 双曲几何：

http://wiki.swarma.net/index.php/%E5%8F%8C%E6%9B%B2%E7%A9%BA%E9%97%B4%E6%A8%A1%E5%9E%8B

 

[6] Word2Vec的相关论文：T. Mikolov, J. Kopecky´, L. Burget,O. Glembek and J. Cˇ ernocky´. Neural network based language models for higlyinflective languages, In: Proc. ICASSP 2009.]

 

[7] DeepWalk算法： Bryan Perozzi, Rami Al-Rfou (2014)."DeepWalk: Online Learning of Social Representations". KDD.

 

[8] 算法的统计物理（张潘总结的非常好的综述材料）：

http://wiki.swarma.net/index.php/2016%E7%A0%94%E8%AF%BB%E8%90%A5%E4%B9%8B%E7%BB%9F%E8%AE%A1%E7%89%A9%E7%90%86%EF%BC%8C%E7%BD%91%E7%BB%9C%E4%B8%8E%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0