文  | 傅渥成

 

今天有位朋友跟我讨论起一个问题，问题大致描述如下：

 

你驾驶汽车开到一条单行道上，你准备去马路尽头的健身房。下雨了，你准备在路边停车，有些车位占了，有些车位空着，你应该用怎样的策略才可以尽可能少淋雨。

 

这是一个有意思的问题，首先马上会想到著名的「摘麦穗问题（1）」，但区别也很明显，摘麦穗时需要找到最大的麦穗，而不是最后的麦穗。在这个问题里，我们需要找到的是最靠近健身房的空车位。怎样才能找到这样的位置呢？

 

作为一个有一点物理背景的人，我接下来马上想到的就是 Fermi 分布，下雨时，大家都想着不要淋雨，于是大家尽可能占据能量较低的能级（距离健身房最近的车位），而由于 Pauli 不相容原理（每个车位只能停一辆车），我们很容易可以得到汽车的分布满足 Fermi 分布：

 

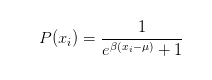
这一分布的大致长相如下图（2）所示，上式中的 β 代表的是温度的倒数（1/kT），在这个问题里，对应于到这个健身房健身的人的强迫症程度，如果大家全有强迫症，都想着必须占一个最靠近健身房的车位，这就对应低温的情况，β 此时取值很大，而如果大家不怎么怕淋雨，就对应于高温的情况，β 的取值很小。图中的 ε 表示能量（能级），对应到停车问题中，有两种理解方法：其一是具体的车位坐标，即公式中的 x_i，其二是，当我们停在该车位后，需要淋雨行走的距离。因为大家都希望淋雨最少，所以大家都希望最小化 x_i，这与物理学中常见的能量极小化是类似的。而 μ 为化学势（Fermi 能），直观地看，大致反映的是从「占据」到「不占据」这样一个转变的转变处。

 

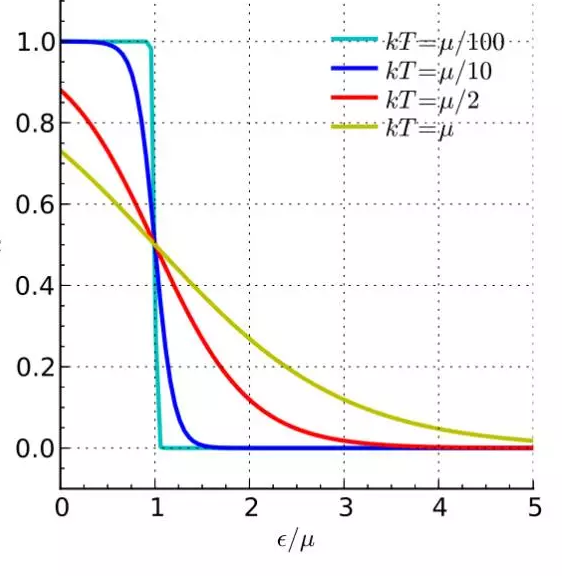
要找到一个合适的停车位，我们就需要对这个分布中的参数（温度和化学势）进行估计，尤其是要估计出化学势 μ 的大小，找出「没车」和「有车」这两种不同分类的车位的「转变点」。如果这个健身房的人全是强迫症的话，这个转变点的位置也就是我们能停车的、最靠近体育馆的位置了，如果大家强迫症轻一点，我们还可以再往里面停停。怎样才能找到这个位置呢？怎样才能判断出大家的强迫症到底轻不轻呢？

 

看到这里，你可能已经意识到了，这个问题已经转变成了一个 Logistic 回归的问题，我们实际上需要建立一个车位「没车」和「有车」的分类器。

 

对于一个特定的车位，如果其满足 Fermi 分布，则该车位有车的概率除以没车的概率可以根据分布函数求得，这个概率的比值也就是传说中的 Logit 的指数版：

 

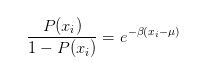
直接求对数，得到 Logit:

 

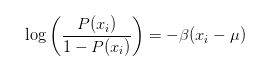
每个车位的 Logit 是大致可以估算的，因为我们可以用肉眼大致看出一个车位的附近是不是足够空，用一个位点附近的有车概率来估计某个位点本身被占据的概率（平均场近似）。接下来的问题就变成了在开车的过程中计算出 β 和 μ。

 

怎样计算 β 呢？其实非常容易，不断计算 Logit，相邻格点一减就好：

 

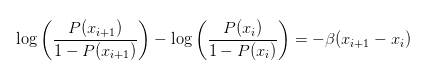
根据这个公式，得到估计的温度（强迫症程度） β，代入到 Logit 的定义中我们还可以把 μ 也确定下来，找到「有车」「没车」这一转变的转变点，这样也就得到了整个 Fermi 分布的分布函数，这些计算就是传说中的 Logistic 回归。

 

接下来也就是确定真正的最低能级了，如果大家全部都有强迫症，那么当然 μ 就会是应该要停车的位置。而如果大家不那么有强迫症，那么开到 μ 处，灵活地再朝前面找找看是不是有空位，如果有空位，停过去应该也就好。

 

References

 

（1）关于摘麦穗问题的讨论参见：http://episte.math.ntu.edu.tw/articles/sm/sm_03_05_1/page2.html

 

（2）文中插图来源：Fermi-Dirac statistics

 

（3）题图来源：Spotted: Terrible parking examples in & around Stafford

 

以上是我对这个问题的理解，一个想法，不一定对。而且这其实不是一个很困难的问题。介绍这样一个问题，并不是希望介绍具体的某种分布或者 Logistic 回归的一些技巧，而是想展示，对于同一个问题，我们可以不断切换「语境」，从而帮助我们对问题有更深刻的理解。而我个人也很喜欢这种问题的讨论，希望有机会借很多这样的小问题沟通起不同学科间的联系。于是，又有人问到另一个问题：

 

如何刻画网络的刻画与传播？这些不同的传播模型会产生什么不同的效果？会出现什么样的临界行为？