文 | 尤亦庄 

 

在我们的世界里，引力支配着宇观星系的运动，量子支配着微观粒子的运动，而智能则支配着我们这些宏观智慧生命的行动。这三种完全不同尺度的现象，看起来似乎毫无关系。但是现代物理学的研究越来越多地表明，它们之间可能有着深刻的联系。

          

虫洞=量子纠缠

 

这第一重联系发生在引力和量子现象之间，称为全息对偶。全息对偶最早是在弦理论的研究中被提出来的[1]。它指的是一个d维空间的量子理论和一个(d+1)维空间的引力理论之间的全息对应，这种对应最明显地体现在量子纠缠和虫洞之间惊人的相似性中。虫洞和量子纠缠分别是引力和量子力学里最神奇的现象，它们都具有非局域的特质。具体来说，虫洞是一种特别的时空结构[2]，它可以将空间中相隔遥远的两个地点联系起来，就像一条时空的隧道。从虫洞两端进入虫洞的两个观察者，最终可以在虫洞内部相遇。而量子纠缠是一种量子力学特有的机制[3]，它可以将两个量子系统关联在一起，使得我们对其中一个系统进行观测以后，不但可以获知被观测系统的状态信息，还可以同时知晓与之纠缠的另一个系统的状态信息。即使两个量子系统相距遥远，只要它们之间建立了量子纠缠，就能实现像“海内存知己，天涯若比邻”一样跨越时空的感应。虫洞和量子纠缠在非局域性方面的这种相似性，启示Maldacena和Susskind提出了ER=EPR假说[4]，也就是虫洞等同于纠缠。当两个量子纠缠的黑洞被分发到不同位置的时候，空间的结构也随之改变：两个黑洞之间将会出现一条连接它们的虫洞，并且随着黑洞的彼此远离虫洞也会被“拉长”。如果解除黑洞之间量子纠缠，那么它们之间的虫洞就会随之断裂。

 

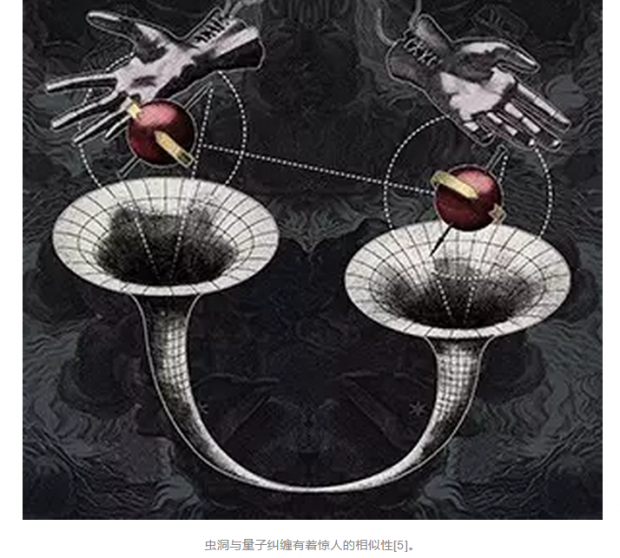
将这一观念推而广之，物理学家们大胆地猜想任何一对纠缠的量子比特之间都有微小的量子虫洞相连。这些微小的虫洞就像时空结构中的丝线，将所有的量子比特维系在一起组成宏观上完整的空间[6]。事实上，量子纠缠的确无处不在：即使在真空中，也充满着瞬息即逝的正反粒子对的量子涨落，它们构成了遍布宇宙的短程量子纠缠，正是它们将空间维系在一起。如果没有这些量子纠缠，空间就会分崩离析。因此可以说，时空结构起源于量子纠缠！这正是全息对偶的核心思想。纠缠结构的改变就会带来时空几何的改变。两个物体之间的量子纠缠越强烈，它们在距离上就会显得越接近。所以说，苹果从树上落向地面的过程，也可以理解为在量子力学的演化下，苹果和地球之间建立了越来越多量子纠缠的过程。从这个角度来看，全息对偶将引力和量子力学深刻地联系在一起。

 

信息蕴于关系之中

 

那么量子纠缠是如何被定量地描述的呢？这就涉及到量子纠缠的本质。量子纠缠本质上是量子信息的一种非局域的存储机制。在经典计算机中，信息都被局域地保存在每个存储单元（经典比特）里。如果我们获得了一份256比特的计算机文件，我们原则上可以确定编码这份文件的256个经典比特分别处于是0还是1的哪一种状态上，每个比特的信息都可以落实到相应的存储单元之上。但是量子信息则不是这样的。如果我们获得了一个由256个量子比特构成的量子态，原则上我们已经知道了这个量子系统作为一个整体的一切性质，但是（有很大可能[7]）我们对其中的任何一个单独的量子比特到底处于哪种量子态仍然是一无所知的。因为这256比特的量子信息可以以高度纠缠的方式分布在所有量子比特的关系之间，从而无法落实到任何一个个体之上。我们可以把一个纠缠的量子系统想象成一张连接着所有量子比特的复杂网络：量子信息分布于网络的连接之间，而不在每个具体的节点之上。任何节点（量子比特）一旦从这个网络中被抽离出来，都会丧失它原先所承载的与其它量子比特相纠缠的那些量子信息。

 

量子纠缠描述的正是量子信息的这种不可分割、不可还原的特点。任何试图将量子纠缠系统的一部分割裂出来的行为，都会导致量子信息的损失。由于信息的损失就意味着无序的增加，也就是熵的产生。因此人们把在一个量子纠缠态中分割出一个子系统所导致的信息损失，作为纠缠的度量，称为纠缠熵[8]。如果以复杂网络的图像来想象量子纠缠的话，那么纠缠熵就应该对应于在大网络中将一个小网络切分出来的时候，所需要切断的连边的数量[9]。事实上，这种直觉的想法是正确的，用来描述量子态的网络在物理学中的准确说法叫做张量网络[10]。人们提出张量网络的初衷是为了更有效地表达量子多体波函数，但随后的研究很快就发现，张量网络的结构正好也是对纠缠结构的一种形象的刻画。两个量子比特之间的纠缠越多，它们在张量网络中的连边权重就会相应地增加，从而拉近它们在网络上的连边距离。这一现象正好符合全息对偶理论中，量子纠缠和空间距离之间的关系！所以说，张量网络为全息对偶提供了一个很好的微观模型：一方面，它描述了量子纠缠态的波函数；而另一方面，张量网络的连边也代表了短程的量子纠缠，同时也代表着将空间联系在一起的微小虫洞，因此整个张量网络的结构便可以解读为全息对偶下的空间几何[11]。

 

如果我们能够对任意的量子态构造出它的张量网络表示，那么就可以看到空间几何是怎么从量子纠缠中演生出来的。然而，这并不是一项简单的任务。当我们得到一个量子态的时候，我们并不能直觉地看出这个量子态背后复杂的纠缠结构。我们所能做的就是对这个量子态做一些测量，并期望在测量数据中寻找关于全息空间几何结构的蛛丝马迹。比如说，我们可以测量一个量子态的各种子系统的纠缠熵。因为不同子系统的纠缠熵，反映了以不同方式来切分张量网络时所需要切断的连边数量，而这一断边数量与网络结构有着紧切关系，因此在纠缠熵的测量数据中蕴含着解读空间几何结构的密码。 

          

深度学习空间结构

 

破译这组密码需要相当的“智慧”。因为对于一个具有256个量子比特的量子态来说，子系统的选取方式就有2^256之多，这个数字可能已经超过了可见宇宙中所有原子的总数。每个不同子系统的选取都可能导致不同大小的纠缠熵，因此这些纠缠熵的数据总量（如果我们可以全部得到的话）也有2^256之多。如何从这组大数据中去发掘隐藏的纠缠结构？我们需要的也许是人工智能，特别是基于深度神经网络的机器学习方法[12]。近年来人工智能技术的飞速发展，已经使我们看到了人工神经网络在大数据挖掘方面的出色表现。不过，神经网络在这里的意义不仅仅是一种挖掘数据的工具，神经网络本身的结构也有着更加深刻的意义。在全息对偶中，我们所希望实现的目标是从量子态的纠缠熵数据出发，寻求能够在最大程度上复现这些纠缠熵的张量网络。这就是说，我们需要不断调整网络的结构和连边权重来寻找最优网络，而这个任务正是基于神经网络的深度学习算法所要做的事情。

 

在最近的一篇来自哈佛大学和斯坦福大学的题为Machine Learning Spatial Geometry from Entanglement Features的预印本论文中[13]，研究者们提出了一种基于深度玻尔兹曼机的算法，称为纠缠特征学习，并演示了从量子纠缠到空间几何的全息对偶。在这个算法中，量子态的一部分纠缠熵被作为训练数据送入玻尔兹曼机，而机器被要求通过对这些训练样本的学习，尽可能准确地预测其余部分的纠缠熵。随着训练的进行，一套神经网络被发展出来。文章进一步证明了该神经网络的结构，正好等同于一个符合纠缠特征的张量网络的结构，因此也代表了演生的全息空间的几何结构。利用这一算法，研究者们展示了包含256个量子比特的一维自由费米子系统在趋于量子临界（CFT2）的过程中，双曲几何（AdS3的空间几何）是如何在学习中演生出来的。

          

宇宙是一张大网

 

复杂网络是引力、量子纠缠和人工智能背后共同的主题。

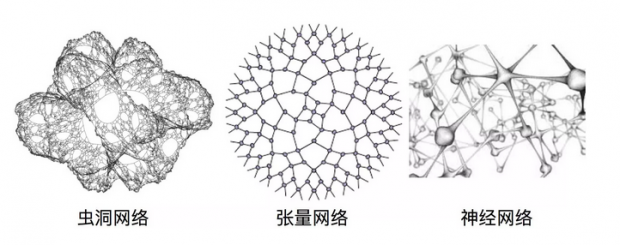
引力、量子纠缠和人工智能正是在这里走到了一起。它们之间涌现出一个共同的主题，那就是复杂网络。在引力理论中，它是描述空间结构的虫洞网络；在量子力学中，它是刻画量子纠缠的张量网络；在人工智能中，它是编码数据特征的神经网络。在这个类比下，我们的宇宙也许可以被看成一个巨型的大脑。它在学习全息量子态的纠缠特征。而我们看到的空间几何正演生于这种学习的过程。当量子态发生改变的时候，宇宙的神经元连接也会随之改变，从而也就改变了空间的几何结构。而当这些几何结构的扰动在宇宙的大脑中传播并抵达地球的时候，我们也许就会说：“哦，这就是引力波！”

 

宇宙就像一张巨大的神经网络，几何演生于学习。

 

参考文献

 

[1] 在历史上，全息对偶是以AdS/CFT的特殊形式提出来的，见E. Witten, arXiv:hep-th/9803131；S.S. Gubser, I.R. Klebanov, A.M. Polyakov, arXiv:hep-th/9802109；Juan M. Maldacena, arXiv:hep-th/9711200。

 

[2] 广义相对论的虫洞解最早由Einstein和Rosen提出，也被称为Einstein-Roson(ER)桥，见A. Einstein and N. Rosen, Phys. Rev. 48, 73 (1935)；另见Physics Focus上介绍此文的科普文章 The Birth of Wormholes。需要指出的是，虫洞也经常在科幻作品中出现，作为超距旅行的一种设想。但在物理学中，可穿越虫洞的形成需要破坏平均零能量条件，如何破坏这一条件还是一个正在研究的问题。

 

[3] A. Einstein, B. Podolsky and N. Rosen, Phys. Rev. 47, 777 (1935)，这篇文章提出了Einstein-Podolsky-Rosen(EPR)对的概念，这也是人们最早认识到的量子纠缠现象；另见Physics Focus上介绍此文的科普文章 What’s Wrong with Quantum Mechanics?

 

[4] Juan Maldacena, L. Susskind, arXiv:1306.0533；或见Susskind随后的一篇关于ER=EPR的讲义 L. Susskind, arXiv:1604.02589；或见Quantum Magazine的科普报道 Wormholes Untangle a Black Hole Paradox。

 

[5] 图片来源于Hannes Hummel for Quanta Magazine。

 

[6] M. V. Raamsdonk, arXiv:1005.3035，这篇文章提出了时空起源于量子纠缠的观念。

 

[7] 考虑一个随机的量子多体态，按照Page定理 D. N. Page, arXiv:gr-qc/9305007，每个量子比特的典型的纠缠熵都接近ln2，这意味着每个量子比特都几乎处于最大混态，也就是说我们几乎不知道任何单个量子比特所处的量子态。

 

[8] I. Bengtesson, K Życzkowski, Geometry of Quantum States: An Introduction to Quantum Entanglement, p301；或见Wikipedia词条Entropy of Entanglement。

 

[9] 纠缠熵与最小截面的关系最早发现于AdS/CFT的意义下，见S. Ryu, T. Takayanagi arXiv:hep-th/0603001。在张量网络中，纠缠熵与网络连边的关系见B. Swingle, arXiv:0905.1317, arXiv:1209.3304。

 

[10] 关于张量网络的综述可见 R. Orus, arXiv:1306.2164；J. Eisert, arXiv:1308.3318；J. C. Bridgeman, C. T. Chubb, arXiv:1603.03039。

 

[11] 基于张量网络的全息对偶在近两年来有很大发展，见 F. Pastawski, B. Yoshida, D. Harlow, J. Preskill, arXiv:1503.06237；P. Hayden, S. Nezami, X.-L. Qi, N. Thomas, M. Walter, Z. Yang, arXiv:1601.01694。另见Quantum Magazine的科普文章 How Quantum Pairs Stitch Space-Time。

 

[12] 深度神经网络的综述可见 J. Schmidhuber, arXiv:1404.7828。

 

[13] Y.-Z. You, Z. Yang, X.-L. Qi, arXiv:1709.01223。

 

尤亦庄（Everett），集智科学家、哈佛大学博士后。文章原载于豆瓣。