冯·诺依曼的手稿《自复制自动机理论》，由人工智能先驱 Arthur Burks 整理成书。集智俱乐部资深粉丝“东方和尚”将全书第一部分翻译成中文，张江做了详细点评。我们将其整理成“冯·诺依曼自动机器理论”系列文章，以飨读者。本文是第六篇（上半部分）。

冯·诺依曼的遗产：寻找人工生命的理论根源

探寻计算的“原力”

神经网络与图灵机的复杂度博弈

　　人工智能如何掷骰子——三种概率理论

　　大数之道——人脑与电脑的对比

　　复杂度阈值与概率论中“漏洞”

       自指机器的奥秘

在前几堂课中，我们讨论的自动机都不是直接对自身进行操作的，因此它们产生的输出与自动机自身具有完全不同的性质。在我提到的三个例子中，这点都很明显。

例如，图灵自动机就可以看作一个包含有限状态的盒子，这个盒子的输出是储存在另外一种实体上，可以简单称为打孔纸带。这条纸带本身并不像图灵机一样具备不同的状态，并能够在状态之间来回切换；此外，与有限状态的盒子不同的是，我们假定纸带是无限长的，因此可以包含的状态也是无限多的。所以，这条纸带从性质上说，同在纸带上打孔的自动机是完全不同的，也就是说，自动机是在完全不同性质的介质上运行的。

对于 McCulloch-Pitts 的自动机模型来说，情况也一样。这里的自动机是由神经元组成的，并且能够向外界产生脉冲信号。这意味着，自动机的输入输出不是神经元本身，而是神经脉冲。当然，这些神经脉冲可以进入周边的组件，并导致完全不同性质的反应。虽然神经脉冲也可以输入到运动系统或者内分泌器官中，导致机械运动或者化学物质的合成，这些输入输出的性质同自动机本身，也就是神经元仍然完全不同。

最后，对于计算机器来说，这个结论也是完全适用的。计算机器可以看成一种被“喂食”并且“吐出”纸带一类介质的机械。不管这种媒介是打孔卡片、磁化的钢丝，还是刻录了许多条平行磁性轨道的磁带，或者是包含黑点的电影胶片，它们都是储存信息的介质，或是用来喂给自动机，或是由自动机产生。这些媒介本身的性质则是和自动机完全不同的。事实上，自动机根本没有产生任何媒介，而是对与自动机本身非常不同的媒介进行了修改。很容易想象在另一种情况下，有一台计算机器输出某种脉冲信号，用来控制完全不同的其他实体。然而即便如此，自动机仍然是同它输出的脉冲本质不同的。在所有这些情况之下，媒介和自动机都存在着实质性的差异。

如果要对自动机的性质进行彻底的研究，我们必须开阔视野，让我们考虑以下的问题：如果自动机输出的是自动机本身的话，这将会怎样？当然，当我们谈论到这个问题的时候就需要小心了。物质上的“无中生有”当然是不可能的。但是我们可以想象在某个环境中有很多零件，自动机可以从中拣起一些零件装配成更复杂的设备；当然，也可以把已有的设备拆散成零件，从而修改成类似于它自己的东西。为了使讨论更清楚，我们需要清晰列出我们所需要的所有基本零件，假设这些零件漂浮于一个大容器里面，并且每个零件的数量都是无穷的。接下来，假设在这个容器中间还生存着一台自动机，它也游弋于这个池塘中，它的主要活动就是不停地收集各种零件，把它们组装在一起；或者把已经组装好的设备拆散成基本零件。

以上对于这种生命的“公理化”定义体系，当然是略嫌粗线条了一些。的确，这样简单地看待一个复杂的问题，当然存在着很大的局限。但是这些局限恰恰就是公理体系本身内禀的局限。我们用这种“粗线条”的体系能够得到的结果，实际上完全取决于我们如何定义基本零件。通常来说，不存在一套确定的规则来指导我们如何选择公理体系中的基本单元，因此这完全取决于体系设计者的常识判断。很难确切地解释为什么一个设计合理，另一个设计却不合理。

首先要排除的一种做法是，我们把每个零件定义得很大，具有很复杂的功能和各种联系。比如就把零件定义成活着的生物体，那么这样就把问题“定义没了”。因为我们的目的就是要通过零件的组合，来描述和理解生命的功能；现在既然定义本身已经包括这些功能在内，那显然就没有什么可以研究的了。所以，如果零件定义得过大，每个零件包含的功能太多太复杂，这样就丧失了问题的意义。

另一方面，如果把零件定义得太小，比如说，规定零件不能大过一个分子、一个原子或者其他的基本粒子，这也不能很好地体现我们所要研究的问题。因为这种情况下，我们就把问题过于还原了。这方面的问题当然也是很重要，很有趣的，然而却同我们打算研究的自动机完全无关。因为我们感兴趣的问题是复杂的生命结构是如何组织起来的，而不是去用量子力学计算化学键能和物质结构。所以，通过以上常识性的分析，大家应该已经理解，研究对象既不能定义得太大，也不能定义得太小。

即使选择了恰到好处的零件尺度，还是有很多种不同定义的方式，也很难说自然地哪一种就比其它的更好。在形式逻辑中，也有过类似的困难：整个系统取决于公理的选择，但是没有确定的法则来规定公理应该如何选取，我们只能依靠我们对于要研究系统的一些常识，并且尽量保证不要把这些公理直接定义成这些问题本身，也不要把其他领域的问题牵扯进来。比如说，在对于几何学建立公理体系的时候，我们应该把集合理论的定理当成现成的直接用。因为我们并不关心集合与数字的转换，也不关心数字与几何的转换。同样，我们也不能将更复杂的比如解析数论中的定理作为几何学的公理运用，因为这样“抄近路”，就导致我们的研究失去了意义。

退一步说，即便公理的设计符合常识，如果由两个不同的人独立地来做这件事，结果往往仍然会大相径庭。比如在形式逻辑中，名词符号的数量几乎和作者一样多，任何人只要使用其中一套符号系统一段时间，就会觉得自己的这套系统会比别人的略高一筹。所以，对于公理体系的应用，零件和符号的选择既非常重要，又非常基本，因此怎样的设计才称得上确切，就不是一件能够严格地判别或者精确地比较的事情了。下面我会说明我对于系统设计的看法，但是我要强调，这只是一个相对主观的陈述。

首先我们想要提出“肌肉”的概念，就像神经元对于大脑一样，肌肉也是自动机的基本零件。也就像 McCulloch 和 Pitts 利用神经自动机理论来抽象实际的神经元一样，在这个定义里，肌肉零件具有连接或者断开连接，提供能量等内在功能。那么，我们就可以在这个定义框架之内，相当简便地描述肌肉、连接组织、断开组织、以及提供代谢能量的组织等，而不用陷入到这些组织的实现细节中去。按照这套思路，约需要 10^(-15) 种这样的基本单元。通过以这种方式来定义自动机，我们已经把问题的一半“丢到窗外”了，而且这可能是比较重要的那一半。我们已经放弃了解释这些零件是如何由实际的基本粒子或者化学中的大分子构成的；而且也放弃了对那些令人着迷的关键问题，譬如自然中的生命零件究竟是如何构成自身的？为什么这些结构有时候是大型的分子，有时候却是大分子的复合？又为什么细胞的尺度总是在微米和分米之间？这对于基本零件来说，是一个很奇怪的尺寸，它离物理上真正的基本尺度，至少还有五个数量级的差别。

这堂课我不打算解释这些问题，而将简单地默认具有这些功能的零件已经存在。那么我们希望回答，或者至少可以进行探索的问题就成了：把这些零件组合成具有功能的有机生命的过程，究竟遵循怎样的规律？这样性质的生命具有怎样的特点，尤其是具有哪些定量特征？以下的讨论仅限于本范围。

复杂度的概念对于我们的讨论是很有用的，但是我们现在也只有一个直观的、模糊的、不全面的、也不太科学的了解。它显然属于信息论这个主题，同热力学领域的知识也有相当的联系。我不知道应该怎样命名这个概念，所以就不妨就把它叫做“复杂度（complication）”吧。这里的复杂度就是指复杂的有效程度，或者说是做事情的潜力。这里我说的并不是一个具体对象牵涉到的复杂程度，而是它有目的地去做事的时候牵涉到的复杂程度。从这个意义上说，具有最高复杂度的对象就是那些可以做很困难的，牵涉很多事情的东西。

我们之所以这样刻画复杂度是因为在研究那些主要功能就是把基本零件组装成其它机器的自动机的时候（包括生命本身和人工的机械自动机），会遇到一件特别的奇事：似乎我们的心智会观察出两种不同的图景（Mind）。你会在这两种不同的图景中切换，也能根据某种图景得到一个显而易见的结论，但是这些结论却是截然相反的！任何人只要对生命稍加观察，便会知道生命可以复制同自身相似的其他生命。这是生命的最常规的功能，如果没有这个功能的话，生命便根本不会存在；或者可以说，恰恰因为复制，才使得生命无所不在。从另一方面来看，生命是由基本零件构成的非常复杂的组合，从概率论或者热力学的角度看，这种组合的出现是极不可能的。生命居然能够存在，这件事本身就是一个了不起的奇迹；而唯一能够使得这个奇迹显得不那么神奇的解释是：生命可以复制自身。因此，如果由于某种特殊原因，一个生命偶然出现了，那么，从此以后，生命就不再被概率法则所束缚，只要环境合适，更多的生命就会跟着出现。然而，从热力学的角度讲，这种“合适的环境”，比起生命本身的存在几率已经要高出很多了（But a reasonable milieu is already a thermodynamically much less improbable thing）。所以，从某种程度上说概率运算在这里存在着一个漏洞（loophole）, 而自我复制的过程恰恰正是利用了这个漏洞。不但如此，比起单纯的自复制，自然界中的生命更胜一筹，因为随着时间的流逝，生命会变得更加精巧。今天的生命是从那些非常简单的生命发育进化而来的。

实际上，生命开始的时候是如此简单，很难想象后来的任何复杂生命的描述，已经被包含在更早的生命之中了。基因这种复杂度比人低一个数量级的东西，是如何蕴含了如此复杂的人类个体的信息的呢？不过也许你会说，因为基因仅仅在人体之中的时候才能起作用，因此它可能并不需要包含将要发生的事情的全部描述，而只要提供几个标记来代表可能的选择就行了。但是，在发育进化史中情况就没那么简单了，因为没有现成的生命个体可以利用。我们知道，一切生物都来自无生命混沌环境中简单的个体，它们逐渐演化出更复杂的东西，这些生命具有产生比自己更复杂之物的能力。另一方面，当我们分析人工自动机的时候，却可以得到截然相反的结论。大家都知道通常一台机器总是比它能够制造出的零件更复杂。因此，一般地说，如果自动机 A 能制造出自动机 B 的话，那么 A 一定包含关于 B 的全部信息，这样 A 才能按照这些信息把 B 制造出来。如此这般，我们就发现，自动机的“复杂度”，或者说它的生产潜力，是不断降级的。也就是说，一个系统的复杂度总是比它制造的子系统要高一个数量级。复杂度是不断降低而非升高的，这个分析人工自动机得到的结论，和上面的分析生命本身得到的结论完全相反。然而我认为，如果将我们对人工自动机的各种知识综合起来，并考虑自动机组合起来产生的效果，就能够消解这个悖论。

在这里，我们并没有向大自然寻找答案，这是因为我们对自然界的生命了解还很少。而另一方面，因为我们自己设计了自动机，所以我们完全了解自动机的性质。不管是实际的人工自动机还是抽象的公理体系所描述的自动机，我们都有足够的信心来设计一种可以复制它们自身的机器。至少从原则上，我们可以说明，为什么从表面上看复杂度的衰退不可避免，但是实际上却不一定如此；并且，复杂的个体的确是可以自动地被比它简单的个体制造出来的。我们的结论是这样的，存在着一个复杂度的阈值，如果系统低于此阈值则它的复杂度就会衰退。这个结论是完全符合我在之前讲座中曾多次提到的形式逻辑中的一些结果的。虽然我们现在对于什么是复杂度以及如何测量复杂度还不甚了解，但是我认为即使我们用最粗糙的衡量标准，也就是系统中所包含的零部件的数量来衡量系统的复杂度的话，本结论仍然成立。如果零件数量少于某一个限度的话，复杂度就会不断下降，也就是说，自动机只能制造比自己简单的自动机；而如果高于这个限度，自动机才能造出同样的，或者更加复杂的新自动机出来。至于这个阈值的具体大小，它就取决于我们该如何定义基本的零件了。在合理定义零件的前提下，我想这个数字也不算小。比如我接下来要说明，如果用十几或者二十几种简单的零件来构造自动机，那么实现自复制至少也需要几百万个这样的零件。虽然我还没有研究其中的细节，但我猜想这样的机器在不算太遥远的未来是会通过我们的艰苦努力而制造出来的。复杂度阈值是一个决定性的临界点，低于它，组装生成自动机的过程就会走向衰退；而一旦超越了这个临界点，组装进化在适合条件下就会发生爆炸性的突变，也就是说每个自动机所制造出来的新自动机都比自己更加复杂，更加具备潜能。

到现在为止，不管怎么解释，这些东西还显得很模糊，因为究竟什么是复杂度，一直没有定义清楚。但是反过来，如果我们不清楚一些关键实例的细节，也就是一些结构究竟是如何展现出复杂度的那种悖论性质的，就不可能给出复杂度阈值合理的定义。不过，这样的困难并不是第一次出现，在物理学发展过程中，人们也曾遇到过类似的问题，如守恒和非守恒量、能和熵等关键概念的提出等。人们必须先对简单的热机和实际机械问题作大量讨论，才能正确地抽象出能和熵的概念。

“生命是什么？”这是一个非常古老的哲学问题，然而，正是对这一问题的探索才催生了今天蓬勃发展的生命科学。细胞生物学、分子生物学、生物化学、生物物理学等等，所有这些学科都是围绕着这个问题展开的。主流的大多数生物学研究都基于这样一种假设：生命这种形态一定是与物质构成有关的，也就是说，只有以碳、氢、氧元素构成的物质才有可能具备生命。在外星生命探测中，科学家们拼命想找到水这种碳基生命存活的基本要求就是这种思想的产物。然而，另外一种不怎么主流的观点认为，实际上生命的本质并不在于物质构成，而在于基本原件的组合方式。所以，按照这种组合方式，我们可以用碳、氢、氧元素去构成，也可以用其它的元素来构成，甚至可以是抽象的数字。这就是人工生命的基本思想，即“生命如其所能（life as it could be）”，而非“生命如吾所识（life as I know）”。因此，生命的本质实际上属于一种“软件逻辑”。如果我们能够透彻地理解了真实的“吾所识”的生命，我们当然可以较有把握地掌握生命的本质，但是，这完全不能阻挡我们直接从“其所能”的纯粹抽象逻辑出发来研究“规范”的生命理论。而这恰恰是冯·诺伊曼研究的出发点，他就是在寻找生命的最小逻辑内核。由于冯·诺伊曼的这种对生命本质的探索实属另类，从而造成了我们对他的研究的理解偏差。很多人非难冯·诺伊曼的研究闭门造车，他不去考察真实生命的运作机制，而是自己创造一套非常不符合现实的自复制自动机。还有的人指出，现在对生物学的研究已经对生命自复制的过程有所了解了，因此冯·诺伊曼做的这些粗糙的假设都可以被扔进垃圾桶了。

首先，我们要知道，冯·诺伊曼研究自复制自动机理论的时候，人们还没有发现 DNA 双螺旋结构（沃森和克里克在 1953 年发现了双螺旋结构，冯·诺伊曼死于 1957 年，而关于自复制自动机的工作多在 1940 年代做出的）。其次，冯·诺伊曼追求的目标与生物学家并不一样。就像是康托尔、图灵、哥德尔等数学家对逻辑本质的追求催生了计算机的发明一样，冯·诺伊曼正在沿着一条规范研究的道路趋近生命的本质。有可能这条道路最终将能创造出与真实生命完全不同的生命形式出来。另外一种对冯·诺伊曼的误解在于冯·诺伊曼所追求的生命本质的软件就是这种可以自复制的程序。而如今这种会自复制的程序已经比比皆是了，它很难和真实生命的复杂性进行类比。

但实际上，如果你仔细读冯·诺伊曼这五篇讲稿就会发现，其实冯·诺伊曼追求的真正问题并不在于自复制本身，而在于“复杂度的阈值”以及概率论中的“漏洞”，他怀疑自复制的自动机恰恰就处在复杂度阈值的边缘，而利用了概率论“漏洞”实现自我复制的。也就是说，其实，这本书里讲的自复制自动机仅仅是冯·诺伊曼为了探索诸如复杂度阈值等概念的一个起点而已。所以，冯·诺伊曼的自复制自动机有点类似于 19 世纪人们讨论的理想模型——卡诺热机。卡诺热机并不能直接用来当发动机使，但是围绕着这个理想模型，人们却能找到“熵”这个物理量的精确科学表述。同样的道理，冯·诺伊曼的自复制自动机的精髓也并不是在探讨自复制问题，而是想围绕着这样一个理想模型而探索复杂度的概念。从这点出发，就不难看出实际上继冯·诺伊曼之后的若干自复制自动机的研究，例如人工生命之父朗顿的环，还有很多自复制的元胞自动机模型其实已经偏离了冯·诺伊曼一开始的初衷。他们更加注重如何实现自复制的结构，而忽视了与自复制相关的诸如复杂度阈值等概念。

个人非常喜欢冯·诺伊曼的这个富有“诗意”的说法，生命就好像是宇宙中物理、数学法则的黑客，专门寻找后门，从而利用它完成自己的复制。而如冯·诺伊曼所言，为什么偏偏是“概率论”中的黑洞，而不是诸如“群论”的漏洞，“解析几何”的漏洞？这说明，冯·诺伊曼已经深刻地认识到生命这种现象是一种“统计的”规律，或者用上一章的语言来说，生命是用一大堆不可靠的原件搭建起来的一台可靠的机器，这台可靠的机器一定会操纵概率法则来“统计地”实现自身的存在。那么，要成功地利用这个概率论中的漏洞，需要具备什么条件呢？在此，冯·诺伊曼就指出了“复杂度阈值”这个条件。也就是说，只有那些能够达到一定的复杂性并且突破了某个阈值的系统才有可能成功的利用“概率论中的漏洞”。

接下来的问题就是，这个复杂度如何度量？复杂度的阈值到底是多少？这两个问题就问到点子上了，因为冯·诺伊曼自己也不知道如何来定义这个复杂度的概念。更不用说如何计算出这个阈值的大小了。不过，冯·诺伊曼还是给出了这样一种定性的描述，“这里的复杂度就是指复杂的有效程度，或者说是做事情的潜力。这里我说的并不是一个具体对象牵涉到的复杂程度，而是它有目的地去做事的时候牵涉到的复杂程度。从这个意义上说，具有最高复杂度的对象就是那些可以做很困难的，牵涉很多事情的东西。”其实，他这里所说的“做事情的潜力”的说法是来源于对一般的自动机的观察：“大家都知道通常一台机器总是比它能够制造出的零件更复杂。因此，一般地说，如果自动机 A 能制造出自动机 B 的话，那么 A 一定包含关于 B 的全部信息，这样 A 才能按照这些信息把 B 制造出来。如此这般，我们就发现，自动机的‘复杂度’，或者说它的生产潜力，是不断降级的。也就是说，一个系统的复杂度总是比它制造的子系统要高一个数量级。”对于这样一种衰退现象的描述，我们都有亲身体会：屋子长时间不扫就会变脏；车子长时间不保养就会出问题；甚至你的计算机长时间不重装系统就会经常死机。所有这些经验都牵扯到一个非常著名的科学定律：热力学第二定律。热力学第二定律说，任何一个封闭的系统最终必然会导致熵增。这里的熵就是指混乱度，所以，任何一个封闭的系统都会朝越来越混乱、无序的方向发展。因此，在这一部分，冯·诺伊曼所说的复杂度概念应该至少可以覆盖熵的概念。它体现出了一种降级、衰退的性质。但是，现实世界中的确还存在着欣欣向荣的一面，生物的进化、科技的进步、经济的腾飞，所有这些方面就体现为复杂度的升级和前进。那么对于这一部分恐怕我们就不能简单地用熵来刻画了，因此，复杂度指标还必须能够描述复杂性的升级。总体来说，我们可以总结出这样一张图：

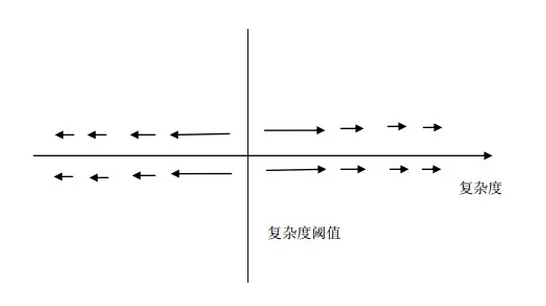
如图所示，这个复杂度阈值就好比是一个排斥子，只要系统的复杂度没有达到这个阈值，系统就会在热力学第二定律的作用下自发地实现复杂度的衰退；而系统的复杂度一旦超过这个阈值，那么也许同样是因为与热力学第二定律类似的作用（冯·诺伊曼在讲后面关于进化的部分，已经暗示了，如果热力学第二定律所主导的扩散是作用在数据描述 Φ(D) 上面的话，那么进化就能产生），那么系统就会呈现复杂度的升级。所以，我们可以断言，复杂度阈值是一种信息论的概念（因此它跟熵、Kolmogorov 复杂性有着异常紧密的联系）。另外，所谓的衰退，自发衰减等效应都跟热力学第二定律有关，所以这也让我们看到了这部分概念实际上与上一章提到的热力学、信息论是紧密结合的。最后，也是最有意思的一点，尽管冯·诺伊曼没有明确指出来的：也许进化与衰退恰恰是一枚硬币的两面。对于突破了复杂度阈值的系统，它就会由于在数据层的扩散和变异作用而不断进化，演化出复杂的结构；而对于低于复杂度阈值的系统，热力学第二定律就会无情地让它衰退、耗散。