译 |    东方和尚

冯·诺依曼的手稿《自复制自动机理论》，由人工智能先驱 Arthur Burks 整理成书。集智俱乐部资深粉丝“东方和尚”将全书第一部分翻译成中文，张江做了详细点评。我们将其整理成“冯·诺依曼自动机器理论”系列文章，以飨读者。本文是第六篇（下半部分）。

冯·诺依曼的遗产：寻找人工生命的理论根源

探寻计算的“原力”

神经网络与图灵机的复杂度博弈

　　人工智能如何掷骰子——三种概率理论

　　大数之道——人脑与电脑的对比

　　复杂度阈值与概率论中“漏洞”

       自指机器的奥秘

冯·诺伊曼描述了八种不同的零件，并用直线来代表它们，且标出了位于中间或者两头的输入和输出端子。自动机在离散的时间下运行，每个零件都要用一个单位的时间做出反应。我们不知道由八种零件构成的这个列表是否完成了冯·诺伊曼的意图，但编者猜想，就此问题，他还没有最后得出结论。

有四种零件是用于处理逻辑和信息的：应激零件（Stimulus organ）是用于接收和发出刺激信号的，并且接收这些信号是相分离的，也就是该零件的真值函数相当于“p 或 q”。合并零件（Coincidence organ）则实现“p 与 q”这个布尔函数。抑制零件（inhibitory organ）则实现“p 与 非 q”布尔函数。激发信号产生器（stimuli producer）则起到刺激信号源的功能。第五种零件是刚体零件（rigid member），这是一种刚性的组件，被用来当作自动机实体的结构骨架。刚体零件不接收任何刺激，它对于信号是绝缘的。刚体零件可以同其它的刚体零件组合起来，也可以用来架设其他的零件。另有一种连接零件（fusing organ），当它受到刺激的时候会把两个零件“焊接”在一起。编者认为连接零件的工作方式如下，假设一个结构上的 A 点将要和另一个结构上的 B 点焊接在一起，这时候连接零件上面活动的输出端子就会同时与 A 和 B 接触，在 t 时刻向连接零件发送一个刺激信号，于是导致 t+1 时刻 A 和 B 两点就会被焊接在一起。然后连接零件就可以离开现场。此外还有切割零件（cutting organ），受到刺激的时候，切割零件就会把连接切开。

第八种零件称为肌肉零件（muscle），可以用来产生运动。肌肉零件一般是刚性的，可以连接到其它的零件之上。如果在 t 时刻肌肉零件受到刺激，在 t+1 时刻它就会收缩到零长度，并保持之上的所有连接。只要刺激信号不消失，肌肉零件就一直保持收缩。编者认为肌肉零件这样工作：比如肌肉零件 1 把一个结构上的 A 点和另一个结构上的 B 点连在一块，肌肉零件 2 又把 A 点和一个连接零件的输出端子 C 连在一起。然后一旦肌肉 1 和 2 都受激发，它们就会收缩，从而把 A、B、C 三点凑在一起，这时候激发连接零件，A 和 B 点就会被焊接起来。最后，当肌肉上的刺激消失之后，它们就会恢复到原有的长度，肌肉１上至少有一个端子也会同 A、B 点分开。至于一开始肌肉和其他零件的连接是怎样实现的，后来又是怎样断开的问题，冯·诺伊曼似乎没有提到。

按照冯·诺伊曼的设想，自动机按照以下的方式制造其它的自动机：在一个平面上漂着母自动机，周围是无穷无尽的零件海。母自动机在存储器中包含有将要制造的子自动机的描述。并按照描述，捡起所需的零件装到正确的位置上去。要做到这点，母自动机必得包含一个能够抓住并且辨认零件的装置。在 1948 年 6 月的课上，冯·诺伊曼对这个问题只是稍微提了几句话：两个激发零件从母自动机上像触角一样伸出来，当它们碰到其它零件的时候，就可以通过激发一个信号去测试所遇零件的性质，如激发零件能够传送信号，而结构零件就不能；肌肉零件受到刺激则会收缩等等。

冯·诺伊曼在他首次的设计尝试中，忽略了能源和能量的问题。他打算之后再考虑这个问题，比如把电池作为一种新的基本零件引入进来。除此以外，冯·诺伊曼的这个早期自复制模型处理了以下的几何动力学问题：包括运动、接触、定位、连接、切断；但是没有考虑真正机械和化学意义上的能量和力的问题。因此把这个模型叫做自复制的动力学模型（kinetic model）；本书的第二部分介绍的是冯·诺伊曼之后提出的自复制元胞模型（cellular model），读者可以对比此两者。

在 1948 年 6 月的课上，冯·诺伊曼提出了动力学自复制模型是否需要三维空间才能实现的问题。他怀疑只有在三维空间或者黎曼曲面（多连接的复数平面）上才能实现该模型。但在本书的第二部分中，二维平面已经足以实现自复制的元胞模型了。这似乎说明，二维平面也足以实现动力学自复制了。

让我们继续回到伊利诺斯的讲座中：冯·诺伊曼讨论了自复制自动机的一般设计方法。他说，在理论上只要有足够的时间和原材料，就可以建立一个能够复制任何机器的车间。这个车间中有一台具备如下能力的机器 B：对于任何一个结构或者机器 X，则机器 B 会自动扫描 X，并把 X 上面的所有零件，以及这些零件的相互连接方式都列成表格，从而得到 X 的完全描述。再根据以上的描述，机器 B 就可以把 X 同样地复制出来。“这同自复制已经非常接近了，因为我们可以把 B 喂给它自己从而得到自己的一个复制品”

但是，相对说来比较简单的，而且同样可以实现最终目的的做法是，不去直接建立能够复制任何给定结构或者样本的自动机，而是去做一个能够根据逻辑描述来组装目标的自动机。因为，按照任何可设想的方式，复制一个对象都必定分成两步，先是从具体实物抽象出描述，然后再从这个描述到具体实物。因此，先做后面这步会比较简单一些。

要做到这件事，我们必先得有一个自动机的公理化描述。如我们所见，我的做法和图灵的通用自动机很像，都是从一个理想机器的通用描述开始。我之前比较含糊地提到过，我们一共有大约十几种基本零件，如果把它们的细节都具体写出来的话（估计两页纸就够了），我们就可以得到一套刻画自动机的无歧义的形式语言。现在，我们可以把这些形式记号转变为二进制，并记录在打孔纸带上面。因此，任何自动机的描述都可以记录在打孔纸带上。我们可以不描述对自动机每一个零件以及这些零件之间的连接方式；而是直接描述这个自动机是如何被一步一步组装出来的，后者会比较方便一些。

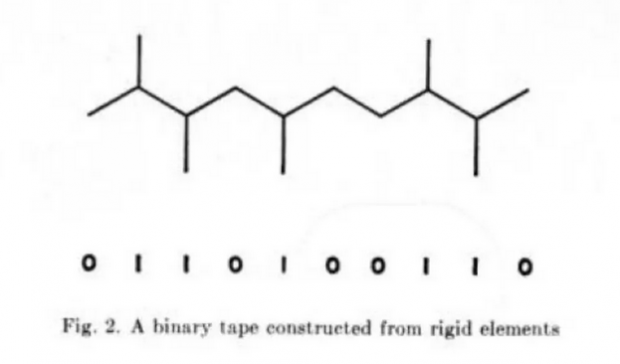
由于我有一种纯数学上的习惯，喜欢把一切东西用最简单的记号表示出来，所以这里的表示可能有些过于简化了。因为我现在用的是二进制表示，所以在上图中，我们不考虑支链的问题，或者说每个位置只能连接一个零件。现有的描述语言和符号系统所用的符号要比二进制更多，但是这里只要用二进制符号就足够了，我们可以毫无困难地表示出更多的符号，只需把支链也分别表示出来，并接上去就行了。其实，我们并不一定要用线性的符号系统。我们也可以用复杂得多的，包括循环的环状结构来表示自动机，但那个时候非线性的代码就不灵了。有理由怀疑我们对于看似简单的串行编码的偏好，只不过是一种来自语言的习惯；很可能存在着非串行的，效率却高很多的自动机描述方式，由于我们对于这类组合却缺乏直觉。

要给出一个完全的公理化描述体系并不太困难，由此我们可以把任何可设想的自动机用二进制代码表示出来。任何这样的描述都可以用类似上图的一串零件来代表。假设自动机 X的符号串是Φ (X)。接下来，我们可以设计一台通用构造器（Universal constructer）A，当我们把Φ (X)喂给 A 的时候，它就能够逐步地利用悬浮在周围的零件，把 X 一点点的组合出来。实际设计工作当然是很麻烦的，但是理论上却是可以办到的。因为这个过程可以归纳为形式逻辑的分步推理，从性质上说，这和通用图灵机并无区别。

还有一件事要说，我之前提到过，要制造一台能够直接复制任何自动机的机器是比较复杂的。所以最好是从要复制的机器的描述而不是从机器的实体来进行复制。但是我想补充一点，存在着某复制机器可以直接拷贝线性的刚体零件链，这是很简单的。因为导致实体复制困难的真正原因是，实体自动机的结构同我们串行的思考习惯完全不同，各种各样的零件朝着各个方向相互连接。仅仅是把已经扫描过的零件排除在列表外，便是很麻烦的事情。但是拷贝一根长链并无这种困难。所以，我可以假设存在一台通用拷贝机器  B(copy automaton)，当我们把任何描述输入 B 的时候，B 就会制造出同样的两份描述出来。

在完成以上两步之后，可能给人一种错觉，在此过程中复杂度衰退的原理似乎仍然没被打破。在表面上看，似乎在复制过程中，既没有产生更微妙的东西，也没有建立更多的联系。A 只能按照描述来制造 X。而按照对于复杂度的一般认识，X 的复杂度是和 X 的描述相等的。另一方面，B 拷贝得到了两份Φ (X)，但是两个同样的事物放在一起，没有理由说它们作为整体的复杂度要高于其中一个的复杂度，并且，我们还需要额外的机器 B 来完成复制。但实际上并不是这样的。

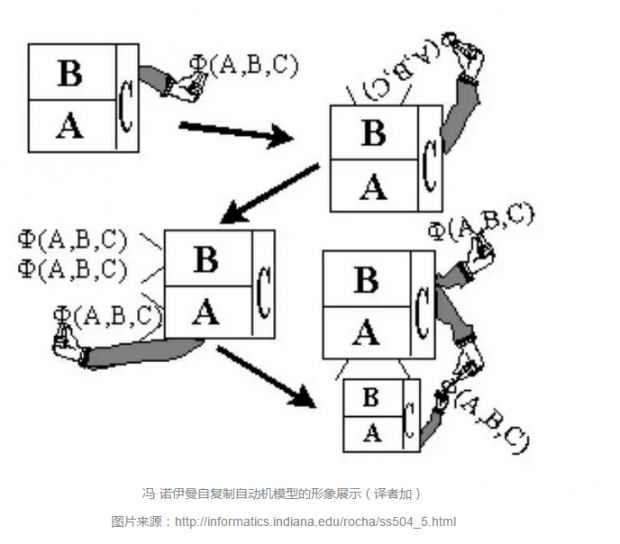
现在我们可以做下面这件事，我们可以把机器 A 和 B 组合在一起，并给 A+B 添加一个控制器 C。C 按照下列方式对 A 和 B 施加控制：C 先命令 B 拷贝两份描述Φ (X)；然后再命令A 按照Φ (X)来实际制造 X，并把其中的 1 份Φ (X)拷贝去掉；最后，C 会把 X 和剩下的那份Φ(X)捆在一起，并把它们从机器 A+B+C 的组合中间分离出去，这样一来，我们就制造出了 X+Φ (X)这样的组合。

按照以上原理，如果我们用（A+B+C）来代替X，并进行上述同样的操作的话，那么(A+B+C)+Φ (A+B+C)的自动机组合，就可以制造出自动机组合(A+B+C)+Φ (A+B+C)出来。因此，自动机自复制得到了实现！

这个过程并不是循环论证：我首先把 A 和 B 做了清楚的定义。在我提到 X 之前，我已经说明，C 可以适用于任何形式的自动机 X。接下来定义了一个变量 X，它描述了 C 将要怎么做，然后，我再让这个变量 X 和 C 产生联系。所以，A、B 和 C 的定义是完全独立于 X 的，在此之后，我再让这个 X 指代 A、B 或者 C。因此，整个过程并非循环。

以上的通用构造器（general constructive automaton）A 具有一定意义上的创造力，也就是说，A 可以从抽象的描述来“制造”出实体的机器来。同样的，通用拷贝机 B 也有一种能够把一份描述变成两份的“创造能力”。但 A 和 B 都不具备自复制能力，此外，控制器 C 也远远没有具备任何形式的创造或复制能力，它唯一能做的就是刺激其它的两个组件去做一些事情，把一些东西连接在一起，或者把一些东西从原来的系统中分割出去。然而，一旦 A、B 和 C 组合在一起，它们作为一个整体却能够复制自身。故而我们可以把一个自复制系统分割成不同的部分，每一个部分虽然都不能够复制自身，但对于自复制机器整体却又都是必不少的。

我们还可以做另外一件事，让 X 代表 A+B+C+D，这里 D 代表任何自动机。那么(A+B+C)+Φ (A+B+C+D)就可以制造出(A+B+C+D)+Φ (A+B+C+D)。换句话说，我们的自复制机器不仅仅有复制自己的能力，还可以顺便生产出其他的组件 D 的能力。这就是任何自复制生命都具备的功能：在复制自身的时候，它还会创造出副产品。

作为一个系统，(A+B+C+D)可以发生类似变异的过程。在定义“自复制”究竟是什么意思的时候，我们会遇到这样的困难：有些结构，比如晶体的生长的确也是在复制自己。但是我们都觉得把晶体称为自复制，显然是名不副实的。有一个办法可以绕过这个困难，就是把发生变异的能力，以及制造类似却不等同于母体的生命的能力包括在“自复制”的定义中间。

现在考虑(A+B+C+D)+Φ (A+B+C+D)这个自动机。“变异”是指中间有一个零件发生随机的变化。如果是 A、B 或者 C 的一个零件发生了变化，那么系统通常就会失去自复制的能力。比如 C 的一个零件被修改以后，C 很可能就不能在正确的时间上给 A 和 B 发射刺激信号，或者无法在需要的时候进行连接和分割，这样的变异就是致命的。

但是如果变异发生在描述Φ (A+B+C+D)上面，那么系统制造出的就不再是它自己，而是修改后的自己，下一代自动机能否继续复制取决于变异发生的具体位置。如果 A、B 或者 C发生了变化，那么子代自动机就会“绝后”。但是如果变异发生在 D 的描述上，那么除了 D变成了 D’之外，变异的子代同母体系统完全相同。之后的子代会把这个变异 D’继承下去。这就是可遗传变异的基本过程。

总之，虽然这套系统还非常原始，但它已经具备了可遗传变异的基本特性。大多数随机变异都是致命的，但是也可能偶尔会发生非致命乃至是可遗传的变异。这是遗传所特有的性质，这套系统也同样具备了。

自指是一个非常古老的话题，它通常与古代奥义以及各种神秘哲学有关。例如佛教中所提倡的“观身无常、观心无我”，以及古希腊的“认识你自己”，都在劝解人们能够将心智的观察箭头指向自己。中国道家所倡导的“无”，正是一个最简单的一字悖论。

一幅最能体现自指深邃含义的图画莫过于这条正在吞噬自己的蛇。此蛇作为一种图腾曾广泛出现在北欧神话、基督教神学、印度教和非洲宗教之中。这条蛇将自指那种深刻的自我毁灭性体现得淋漓尽致——我们可以想象一下当它把自己吞噬完毕会产生怎样怪异的情景。

将这种自我毁灭性的古代奥义应用到现代科学中已经产生了一系列深刻的结论。首先，在19世纪末，著名数学家康托尔（George Cantor）将“对角线删除”法则应用到集合论中，从而证明了实数的个数比自然数多。紧接着，罗素（Bertrand Russell）提出了著名的“罗素悖论”而摧毁了弗雷格（Gottlob Frege）的数学大厦。年仅25岁的哥德尔（Kurt Gödel）巧妙地应用同样的破坏性自指一举摧毁了数学大师希尔伯特（David Hilbert）的完备一致性的数学体系梦想。图灵（Alan Turing）则利用同样的技巧进一步发现任何超级计算机都不可能求解的图灵停机问题。

纽约时报曾将哥德尔不完备定理评价为20世纪最伟大的数学定理。自指可以用来构造破坏性的悖论已经是众人皆知、司空见惯了。然而，这种认识其实很片面。自指包含了比自指悖论更宽泛的内容，因为在自指大家庭中，还包括另外一类构建性的成员。

1953年，正当人们举杯欢庆沃森和克里克发现了DNA双螺旋结构，并从分子层面上解释了生命的自我复制之谜的时候，另外一名伟大的美国匈牙利裔数学家：约翰.冯诺依曼（John von Neumann）正在独立地思考着生命自我复制的逻辑基础。然而，令人遗憾的是，那时的冯诺依曼已经患上了癌症，并于1957年的2月去世。于是，他的助手阿瑟.伯克斯Arthur Burks将他关于自复制自动机理论的整理成书《Theory of Self-reproducing Automata》，并于1966年出版。

与沃森.克里克不同的是，冯诺依曼要寻找的是生命自我复制的逻辑基础而非物质基础。虽然冯诺依曼没有明确指出，但是已经暗含了这个自复制的逻辑基础不是别的，正是一种自指结构。也就是说，自指恰恰是生命实现自我复制的逻辑内核。这也许会让读者感到困惑。不是说，自指都是用来构造诸如哥德尔定理、罗素悖论之类的破坏性武器吗？实际上，还存在着另外一大类自指，笔者称之为“建构性的自指”，它不但不会引起破坏，反而能够创造很多令人意想不到的惊奇结构。至于自我繁殖的系统是如何令人意想不到的，请参考第4节的讨论。

实际上，早在1938年，与哥德尔共同奠定递归函数论基础的数学家克林尼（Stephen Kleene）就证明了递归函数论中的一个著名定理：递归定理（更精确地说，应该叫Kleene第二递归定理）。根据它，人们可以很轻松地得到一个数学推论，系统的自我复制是可能的。证明递归定理的核心技巧，是一个被称为“蒯（kuai3）恩”的特别技术。蒯恩（Willard.V. Quine）是美国的哲学家，终身致力于哲学、数理逻辑、集合论的研究。他创造了一种称之为蒯恩的方法，使得人们可以不通过使用“我”或者“这句话”等词语就能创造出可以谈论自身的句子来。

有趣的是，蒯恩构造恰恰就是那条“黄金对角线”（这一方法正是当年康托尔最早提出证明实数比自然数多的方法，也是哥德尔定理构造哥德尔句子的关键技术）。只不过，康托尔、哥德尔等人的对角线与蒯恩的对角线方法稍有不同。我们会在第6节中详细地讨论这些技术。    

总而言之，从宗教到科学，从悖论到自复制，自指是贯穿始终的主题。正如《哥德尔、艾舍尔、巴赫》这本书指出的那样，自指是一条永恒的金带。

于是，一切的矛头都指向了这个神奇的复杂度阈值，它到底是多少？虽然冯·诺伊曼到死也没有给出任何关于复杂度的计算，但是他用一名数学家和哲学家敏锐的头脑，深刻地指出了其实这个复杂度阈值与数学、逻辑学以及哲学上的一个重要概念“自指”有关。

冯·诺伊曼在本章最末部分所讨论的能够自复制的自动机的抽象描述：(A+B+C)+Φ (A+B+C)其实就是一个哲学家们称之为“蒯恩”的程序。蒯恩（Willard.V. Quine）是一位美国的哲学家，他创造了一种称之为蒯恩的方法，使得人们可以不使用“我”或者“这句话”等词语就能创造出可以谈论自身的句子来。例如下面这句话就是一句不使用“这句话”的自指悖论：

把“把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的”中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变得到的句子是假的

当你按照这句话的指示将引号中的文字放到引号后面的时候，你就得到了一句自我否定的句子，所以上面那句话与下面的话等价：

这句话是错的

之后，数学家 Kleene 将蒯恩这种语言上的操作进行数学化就得到了一种更加普适的Kleene 递归定理。有了这个递归定理以后，数学家就可以在严格的数学公理体系中玩各种各样的自指游戏。之后，哥德尔利用这种技术构造了公理系统中著名的哥德尔句子“本命题不可证明”，从而推出了哥德尔定理这个被纽约时代杂志评选为 20 世纪最伟大的数学定理。

那么，究竟这个蒯恩程序是什么呢？其实，它非常容易理解，它就是一个能够把自己的源代码打印出来的程序。

S (x){

q=’S(x){n q=’’+q+’’;n Print(’’+p(q)+’’);n}’;

Print (‘S(x){n q=’’+q+’ ’;n Print(’’+p(q)+’’);n}’);

}

这里面的“n”表示换行符，即如果执行 Print(‘AnB’)，则程序会输出下面的字符串：

A

B

“+”表示将两个字符串进行串联形成一个新的字符串，例如 A=’123’,B=’456’，则A+B=’123456’。

这个自打印程序调用了一个简单的解码函数 p(q)，p 的作用是将字符串 q 变换成更浅一层次的字符串。例如，如果 q 是“’’n”，那么 p 这个函数就会计算输出“’’n”。也就是说 p 完成了一组映射：它把“”映射成“”，把“’”映射成“’”，而把“n”映射成回车符。显然 p 是可以写出来的。大家可以利用 java 或者 VB 来实现这个程序，运行它就会发现它能够自我复制。

让我们来分析一下这个程序是如何运作的。首先，看程序的最后一行，即

Print (‘S(x){nq=’’+q+’ ’;n Print(’’+p(q)+’’);n}’);

这句话的作用是让程序在屏幕上打印出一个字符串。注意观察，这个被打印出的字符串其实是由“+”号被分割成了 5 个部分，第一部分是“S(x){nq=’”，第二个部分是 q 这个字符串的原封不动的拷贝，第三部分是字符串：“’;n Print(’”，第四部分是函数 p 作用到 q 上面的结果即 p(q)；第五部分还是一个字符串：“’);n}”。然后当我们把 q 字符串的数值代入第二部分和第四部分，并进行运算 p 之后，就得到了和源程序一模一样的结果。你不妨在计算机上运行这段程序，就会发现这段程序会在屏幕上赤裸裸地把自己的源代码打印出来。

我们不妨把这段程序的 5 个部分进行归并，写成由下面的三部分构成的Copy。Popup。Control，其中 Copy 就是 5 部分中的第二部分，即相当于一个拷贝字符串的程序，你输入给 Copy 什么字符串，Copy 就会把那个字符串再原封不动地吐出来；Popup 这部分就是原来的 5 部分中的第四部分，即函数 p，它的作用相当于一个弹出操作，也就是为输入的字符串脱去一层引号。如果输入的字符串原来是在第 n 层虚拟世界，则 Popup 的作用就是让字符串跳到第 n-1 层；最后 Control 这部分就相当于原来的第 1、3、5 这三部分以及最一开始的语句 Print 的总合，它的作用就相当于是为 Copy 和 Popup 制造出来的字符添加适当的连接词，使得最后的字符串能够拼接成与原来的程序一模一样的源程序，并将其打印到屏幕上。所以这句“Print (‘S(x){n q=’’+q+’ ’;n Print(’’+p(q)+’’);n}’);”就可以改写成(Copy 。 Popup 。Control)(q)。其中“ 。”表示将不同的程序连接为一体。

如果我们把一个计算机程序 X 的描述（或者称源代码）写为Φ (X)，则自打印程序的第一条赋值语句就相当于给 q 赋予了Φ ((Copy。 Popup。 Control))，即(Copy。 Popup。 Control)这三个程序连在一起的源代码。最后我们可以将自打印程序简写为：

S(x){

q=Φ (Copy。Popup。Control)(Copy。 Popup。Control) (q);

}

那么，观察这个程序，就会发现实际上它就是冯·诺伊曼所说的那个自复制程序：(A+B+C)+Φ (A+B+C)了。在这里 Copy 就相当于冯·诺伊曼程序中的拷贝器 B，它能将输给它的数据原封不断地再打印出来；Popup 就相当于冯·诺伊曼说的通用构造器，它能够根据一段数据而把数据对应的自动机的源代码打印出来（这相当于从描述中构造出自动机）。Control 这部份就对应了C。而 q=Φ (Copy。 Popup。 Control)就对应了描述：Φ (A+B+C)。因此，我们实际上可以很容易地用我们的个人电脑实现自复制的计算机程序。

你也许会提出这样一个质疑，即使是这个蒯恩程序也没有实现真正的自复制。因为这个程序仍然需要调用一些字符串处理程序例如函数 p，以及字符串运算符“+”等等，而这些功能并不是这个程序自己完成的，而必须借助比它更高一层的编译器才能完成。于是，这个蒯恩程序实际上已经与一个平庸的自复制程序（例如就包含了一个平凡的高层次语句”Copy me”）没有任何区别了，只不过对于平庸的自复制程序来说，我们为自复制的环境赋予了过高的能力，而自复制程序本身只起到一个触发器的作用。而对于蒯恩程序来说，翻译蒯恩程序的环境变得相对简单一些，但是实现自复制的代码就要承担更大的责任。原则上讲，我们的确不能做出来一个完全不借助于环境，而凭空实现自复制的机器。但是，我们总可以降低对环境的要求，把编译器的复杂度变小，从而凸现出自复制程序的能力来。

由此我们可以看出，在不同的情况下，编译环境和在此环境下实现的程序会呈现出连续的复杂度变化。而自复制程序实际上是对环境的复杂性和程序本身的复杂性的一种折衷。因为如果环境的复杂性越高（编译环境可以支持很复杂的指令集合），要实现一个可以打印自身源代码或者复制自身的程序就变得很简单（程序自身的复杂度下降）；反过来，如果环境的复杂度越低，那么你要实现一个自复制的程序也会变得越困难。于是，我们可以得到下面这张图：

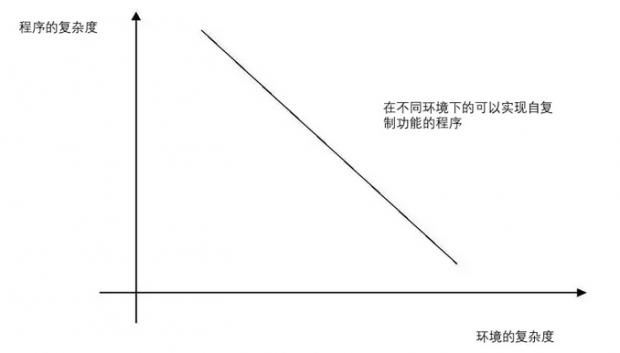
如图所示，如果我们把一切程序按照它所运行的编译环境以及它自身的复杂程度列出这样一个连续的空间，那么在不同的编译环境下的自复制程序就会近似地形成一条如图的直线。我们可以肯定地知道，它是一条单调下降的曲线，因为随着环境复杂度的升高，要实现自复制的程序的编写也会变得越来越轻松。所以，我们大概可以估计出来这样一个自复制程序所满足的复杂度方程：

上述公式表示了实现自复制程序的复杂度的允许条件，当等号成立时，它就对应了图中的向下的直线。不等式对应了直线右上角的半平面。这个式子让我们联想到了第二章提到的不确定性原理。因此，自复制程序的复杂度讨论也许的确存在着类似量子理论中的不确定性原理。这种从不同层次来考虑程序复杂度的概念也许真的蕴藏着我们尚不知道的真理。

总之，我认为自复制自动机才真正抓住了人们常说的“涌现”这个关键概念的本质。因为从单个组成单元来看，无论是通用构造器 A，还是拷贝器 B 还是控制器 C，以及它们的数据Φ (A+B+C)都不具备自复制的功能，而当把它们恰当地合在一起的时候，它们的确可以实现自复制，从而实现了自复制功能的涌现。与其它对涌现的机制讨论的不同之处在于，自复制自动机具有相应的数学对应物：递归定理，因此我认为如果要从数学上理解涌现，自复制自动机是绕不开的。只可惜，冯·诺伊曼的最终梦想：从热力学和信息论的角度来理解自复制自动机的自发涌现仍然没有实现。

关于蒯恩、递归定理以及自指更多的讨论请参看本人写的科普文章：《系统中的观察者（5）——自指——一条连接图形与衬底的金带》http://wiki.swarma.net/index.php/%E7%B3%BB%E7%BB%9F%E4%B8%AD%E7%9A%84%E8%A7%82%E5%AF%9F%E8%80%85(5)%E2%80%94%E2%80%94%E8%87%AA%E6%8C%87（或点击阅读原文）。以及更多的参考书，包括：侯世达：《哥德尔、艾舍尔、巴赫》，商务印书馆，1996；R.M. Smullyan: Diagonalization and Self-Reference,Oxford University Press, 1994。