文 | 张江

自指是一个非常古老的话题，它通常与古代奥义以及各种神秘哲学有关。例如佛教中所提倡的“观身无常、观心无我”，以及古希腊的“认识你自己”，都在劝解人们能够将心智的观察箭头指向自己。中国道家所倡导的“无”，正是一个最简单的一字悖论。

一幅最能体现自指深邃含义的图画莫过于这条正在吞噬自己的蛇。此蛇作为一种图腾曾广泛出现在北欧神话、基督教神学、印度教和非洲宗教之中。这条蛇将自指那种深刻的自我毁灭性体现得淋漓尽致——我们可以想象一下当它把自己吞噬完毕会产生怎样怪异的情景。

将这种自我毁灭性的古代奥义应用到现代科学中已经产生了一系列深刻的结论。首先，在19世纪末，著名数学家康托尔（George Cantor）将“对角线删除”法则应用到集合论中，从而证明了实数的个数比自然数多。紧接着，罗素（Bertrand Russell）提出了著名的“罗素悖论”而摧毁了弗雷格（Gottlob Frege）的数学大厦。年仅25岁的哥德尔（Kurt Gödel）巧妙地应用同样的破坏性自指一举摧毁了数学大师希尔伯特（David Hilbert）的完备一致性的数学体系梦想。图灵（Alan Turing）则利用同样的技巧进一步发现任何超级计算机都不可能求解的图灵停机问题。

纽约时报曾将哥德尔不完备定理评价为20世纪最伟大的数学定理。自指可以用来构造破坏性的悖论已经是众人皆知、司空见惯了。然而，这种认识其实很片面。自指包含了比自指悖论更宽泛的内容，因为在自指大家庭中，还包括另外一类构建性的成员。

1953年，正当人们举杯欢庆沃森和克里克发现了DNA双螺旋结构，并从分子层面上解释了生命的自我复制之谜的时候，另外一名伟大的美国匈牙利裔数学家：约翰.冯诺依曼（John von Neumann）正在独立地思考着生命自我复制的逻辑基础。然而，令人遗憾的是，那时的冯诺依曼已经患上了癌症，并于1957年的2月去世。于是，他的助手阿瑟.伯克斯Arthur Burks将他关于自复制自动机理论的整理成书《Theory of Self-reproducing Automata》，并于1966年出版。

冯·诺依曼的遗产：寻找人工生命的理论根源

探寻计算的“原力”

神经网络与图灵机的复杂度博弈

　　人工智能如何掷骰子——三种概率理论

　　大数之道——人脑与电脑的对比

　　复杂度阈值与概率论中“漏洞”

       自指机器的奥秘

与沃森.克里克不同的是，冯诺依曼要寻找的是生命自我复制的逻辑基础而非物质基础。虽然冯诺依曼没有明确指出，但是已经暗含了这个自复制的逻辑基础不是别的，正是一种自指结构。也就是说，自指恰恰是生命实现自我复制的逻辑内核。这也许会让读者感到困惑。不是说，自指都是用来构造诸如哥德尔定理、罗素悖论之类的破坏性武器吗？实际上，还存在着另外一大类自指，笔者称之为“建构性的自指”，它不但不会引起破坏，反而能够创造很多令人意想不到的惊奇结构。至于自我繁殖的系统是如何令人意想不到的，请参考第4节的讨论。

实际上，早在1938年，与哥德尔共同奠定递归函数论基础的数学家克林尼（Stephen Kleene）就证明了递归函数论中的一个著名定理：递归定理（更精确地说，应该叫Kleene第二递归定理）。根据它，人们可以很轻松地得到一个数学推论，系统的自我复制是可能的。

证明递归定理的核心技巧，是一个被称为“蒯（kuai3）恩”的特别技术。蒯恩（Willard.V. Quine）是美国的哲学家，终身致力于哲学、数理逻辑、集合论的研究。他创造了一种称之为蒯恩的方法，使得人们可以不通过使用“我”或者“这句话”等词语就能创造出可以谈论自身的句子来。

有趣的是，蒯恩构造恰恰就是那条“黄金对角线”（这一方法正是当年康托尔最早提出证明实数比自然数多的方法，也是哥德尔定理构造哥德尔句子的关键技术）。只不过，康托尔、哥德尔等人的对角线与蒯恩的对角线方法稍有不同。我们会在第6节中详细地讨论这些技术。

总而言之，从宗教到科学，从悖论到自复制，自指是贯穿始终的主题。正如《哥德尔、艾舍尔、巴赫》这本书指出的那样，自指是一条永恒的金带。

提到自指，很多读者马上就会联系到那句臭名昭著的悖论句子：

这句话是错的

这句话之所以让人讨厌，是因为你无论从正面（即假设它是对的），还是从反面（即假设它是错的），都会得出相反的结论。因此，这句话既不对也不错。

然而，这句“说谎者悖论”仅仅是广大自指语句家庭中的成员之一，有很多语言是自指的，但却是无害的甚至是有益的。比如下面的句子：

这句话是对的

这句话就是一个既可以是对又可以是错的句子。你可以非常虔诚地承认这句话所论述的内容是对的，然后，再看它的内容，它正在陈述：它自己是对的。于是你初期的假设被证实了。另一方面，当你假设它是错误的时候，你就会知道它的语义“这句话对”是错误的，于是你就真的得到了这句话就是错误的结论。也就是说这句话的对错完全取决于你的假设。

当然，还有一些更好玩的自指句子，如：

这句话有2个‘这’字，2个‘句’字，2个‘话’字，2个‘有’字，7个‘2’字，11个‘个’字，11个‘字’字，2个‘7’字，3个‘11’字，2个‘3’字

这被称为自描述语句，也就是说这个句子正在描述自己的“分子”构成。当你尝试独立写下这样一个自描述语句的时候就会发现，你其实并没有创造这句话，而是这句话正在“迫使”你写出它自己。这是因为，按照这个句子的逻辑一旦你开始写下第一个字，你就必须按照已出现的字的情况而自动补全后面的句子。同时，这个语句还具有了不起的自我修复性。你不妨将该句子中的某一个汉字删掉（例如你删除第一个‘2’字），就会很快发现该句子中的一部分出现问题了，即“7个‘2’字”是错误的。因此，你会根据句子整体的意思指导而发现你少了一个‘2’字。

因此，自指不都是破坏性的，更多的自指是无害的，而且可以给我们带来一定的“惊奇性”。这种惊奇性的来源主要是自指语句中包含的无穷递归，因为它可以创造无限的虚拟层次。

虚拟层次是一个我们司空见惯的概念，例如故事中的故事，电影中的电影，梦境中的梦境等等（电影《盗梦空间》（Inception）就是对梦中梦层次的一个非常好的展示）。在上一章中，我们已经领略了程序是可以通过模拟而产生多个虚拟层次的。在语言中，我们不妨将引号看作是标识一个新的虚拟层次出现的符号。这样，下面这句话：

“明天会下雨”是错的

就包含了两个层次，更深一层的句子是“明天会下雨”，而上面一层则是“‘明天会下雨’是错的”。当然，我们通过不断地加引号就能创造出各种复杂的嵌套结构。

另外，人们发明了一类代词可以指代不同的句子。例如“这句话”，“那句话”。这些代词就仿佛是一个指针会将一个句子整体放到一个引号中而实现多个层次的嵌套。例如下面两句话：

下面的句子是对的

明天会下雨

在第一句话中出现了一个指代词“下面的句子”，它是一个指针指向了“明天会下雨”这句话，于是我们观察者作为一个解读器就会将这两句话解释为：

“明天会下雨”是对的

也就是说，我们照指代词的意思将“明天会下雨”这句话加上了引号放到了第一句中的“下面的句子”那个指代词之中了。于是，指代词创造了包含了两个虚拟层次的句子。

按照同样的逻辑，当我们遇到了指代词“这句话”的时候会发生什么呢？我们将会得到一个包含无穷虚拟层次的语句。例如我们将自指语句“这句话是错的”按照代词的法则展开就会得到：

““““…………”是错的”是错的”…………”是错的”是错的

我们看到，只要“这句话”这个指代词一出现，我们就能够得到无穷。因此，自指语句往往都与无穷虚拟层次有关。注意，我这里用的词语是“往往”，而不是“一定”。之所以这样说，是因为的确存在着一种构造自指语句的方法，让我们绕过无穷。这种方法就是大名鼎鼎的蒯恩法。

在讨论蒯恩之前，让我们先来领教句子中的动词（动词短语）。大部分动词是与我们读句子的观察者无关的，例如：

小明起床了

这个句子表达了小明这个人物正在做的一个动作是起床了。其中“起床了”就是一个动词。当然，有很多动词不仅可以描述一个人或者事物，还可以去描述句子，例如：

“小明起床了”包含5个字

这里面的“包含5个字”就是一个描述句子“小明起床了”的动词。还有一些句子包含了动词，而这个动词是使役我们读这个句子的观察者做出某种动作的：

删除“小明起床了”中的第一个字

这个“删除第一个字”的动作就是使役读句子的观察者做出的，于是，我们按照这个句子的说法进行操作，就会得到一个新句子：

明起床了

我们可以再做稍微复杂一点的操作，例如：

把“小明起床了”中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

按照这个句子所描述的复杂操作（你最好拿来一个草稿纸，自己在纸上写一写），我们就可以得到：

小“小明起床了”明起床了

好，既然你已经熟悉了这个复杂的操作，那么让我们来看下面一个古怪的句子：

把“把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变”中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

如果按照这个句子指示的操作你会得到什么？让我们来做一做。按照这个句子的要求，我们可以把引号之中的句子施行下面的三步操作：第一步，把第一个字，也就是“把”放在左引号前面，这样就得到的新句子中的第一个字：“把”；第二步，将后面的字放在右引号后面，这样新句子就会以“中的第一个字放到……字不变”为结尾；第三步，保持引号和其中的字不变，于是新句子的中间会有一个引号，并且引号的中间就会是“把中的第一个字放到……”。于是，我们得到的新句子就是：

把“把中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变”中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

请注意，这个新句子和原句子是一模一样的！事实上，原句子使役我们观察者完成了一次对自己的拷贝！这个句子其实就是大名鼎鼎的蒯恩了！

也许，你已经有些糊涂了，让我们再好好看看究竟蒯恩是怎么操作的。首先，我们定义了一种具有动词的句子，也就是：

把“X”中的第一个字放到左引号前面，其余的字放到右引号后面，并保持引号及其中的字不变

虽然提起自指，人们很容易想到自指悖轮。但是，人们不熟悉的是另外一大类无害的自指，它们通常直接应用蒯恩技术，而实现某些意想不到的结构或者功能。下面，让我们先从一种最简单的建构性自指：自打印程序说起。

所谓的程序自打印就是指一个程序能够在不读取外部文件的条件下把自己的源代码打印出来。首先，我们要先领教一下，一个自我打印的程序是多么不可能的！我们知道，要写一个程序打印出“helloworld!”字样是非常容易的，例如：

Print(‘helloworld!’)

注意在这个程序中，字符串都用单引号括起来。那么，我们能不能写一个程序，把这个打印“helloworld!”程序的源代码打印出来呢？这也是可以办到的，例如下面的程序：

Print(‘Print(’helloworld!’)’)

注意，这里面的“’”会被编译器解释为一个字符串，这个字符串中就有一个字符：“ ` ”。采用这个技巧，我们就可以解决如何在一个引号之中再输入一个引号的问题了。所以，我们可以很轻松地打印出这个能够打印”helloworld!”程序的程序源代码出来。但是很显然这个程序并不能打印出它自己，也许你会想到能不能打印出上面的程序源代码出来？当然可以！

Print(‘Print(’Print(’helloworld!’)’)’)

其中就表示包含一个字符“”的字符串变量，这样Print(‘’)就会打印出一个字符“”，而Print(‘’’)就会打印出字符串“’”出来。所以，引号里面可以放入任意层次的引号。

但是这个程序仍然不能打印自己！你很快发现，我们人类是写不出这种能够打印自己的程序的，因为它包含了无穷递归。不过，通过蒯恩技巧，实际上我们完全可以写出来一个自打印程序，如下：

S(x){ q=’S(x){n  q=’’+q+’’;n 
 Print(’’+p(q)+’’);n}’;
 Print(‘S(x){n  q=’’+q+’’;n  Print(’’+p(q)+’’);n}’); }

源代码1：自打印程序源代码

这里面的“n”表示换行符，即如果执行Print(‘AnB’)，则程序会输出下面的字符串：

A

B

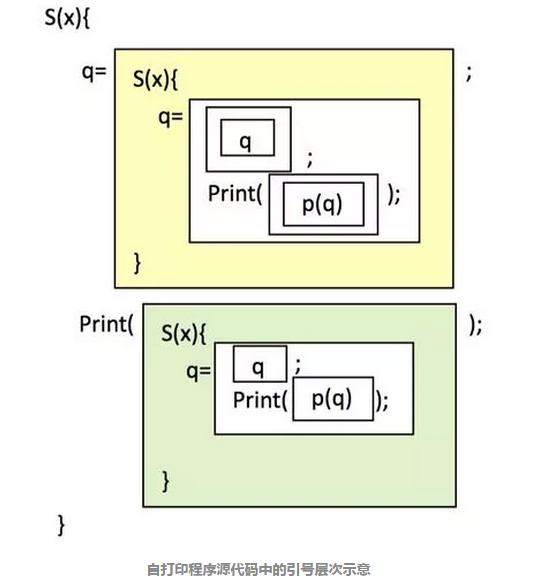
如上图，这个自打印程序中的引号全部用方框来替代。这样第一层引号’…’就对应了第一层的方框，引号中的引号，即“’…’”就对应了框中的一个框。这样，由于程序中出现最多的层次是四层引号，即“’”，所以上图中就出现了第四层框。

另外，我们还观察到，这个程序包含了两个大框，即“q=”后面的黄框和“Print()”之中的那个蓝框。这两个框的结构是完全一样的，只不过黄框比蓝框多了一个虚拟层次，这反映在所有的蓝色框中的最深一层框都再加上一层框就得到了黄色框。

更有趣的是，整个程序S(x)实际上和这两个框是相似的，因此这个程序本身就是一个分形结构。在传统的分形结构中，每一个部分都会包括无穷多的细节。但是，在这个自打印程序中，虽然有嵌套的分形结构，但是却没有达到无穷，最深的引号也仅仅有4层。

S(x){ 
q= λ (Copyo  Popupo  Control) 
(Copyo  Popupo  Control)(q); }

源代码2：自打印程序的源码缩写

在此小节中，我们用自打印程序和自复制程序为例来说明了建构型的自指。然而，建构性的自指实际上不仅仅是这两种，它还会有各种各样的用途。

未完待续：http://wiki.swarma.net/index.php/%E7%B3%BB%E7%BB%9F%E4%B8%AD%E7%9A%84%E8%A7%82%E5%AF%9F%E8%80%85(5)%E2%80%94%E2%80%94%E8%87%AA%E6%8C%87让苹果砸得更猛烈些吧！