
作者:Albert-László Barabási
原文:Love is All You Need——Clauset's fruitless search for scale-free networks
翻译:辛茹月
校稿:集智小仙女
日前,无标度网络模型的发现者 Barabási 撰写长文,激烈地回应两位来自科罗拉多大学的学者的质疑。他们的论文《无标度网络是罕见的》,认为在真实网络中,幂律并不是普遍存在的,他们试图挑战无标度网络的范式。Barabási 对这篇论文的概念界定、技术方法、判断标准都做出反驳,直言这项研究是失败的,无标度网络理论并未受到威胁。
1.Barabási:
对无标度网络的质疑是无效的
过去几周里,很多人希望我能回应 Anna D. Broido 和 Aaron Clauset (以下简称BC)的预印本论文《无标度网络是罕见的》(以下简称 BC 文章),以及他们在 nature 上发表的关于无标度网络的研究。

这篇文章的思想简单而又有欺骗性:它从教材上定义的无标度网络的度分布满足幂律分布[2]出发,对927个网络进行幂律拟合,发现只有4%的网络是无标度的。因此作者就把结论“无标度网络是稀少的”(Scale-free networks are rare)作为文章的标题,来最大程度的吸引大众的注意力。
这种吸引眼球做法确实奏效,《Quanta》杂志毫无保留地接受了这个结论。在《大西洋月刊》刊登了《真实世界网络中幂律的普遍性被质疑》这篇文章后,这个未经评审的预印本论文曝光在公众面前,而当初无标度网络的发现却从未享受过这种待遇。
当我看到手稿概念上的问题时,我想这篇文章在技术上一定是成熟的。然而,当我深入阅读这篇论文,就发现它的论证缺乏说服力。如果你有足够的耐心看完我这篇评论,你就会发现,这篇预印本论文在概念和技术上,都有严重的失误。
概念问题
2.无标度网络的发现
首先,让我们总结一下关于无标度网络的大量工作,这对于理解Anna D. Broido 和 Aaron Clauset 的论文(下文简称 BC文章)推出的结论至关重要。
首次发现。无标度网络的性质在1999年被发现,独立的存在于自治系统[4]的WWW[3]和互联网中。实证观察非常简单:这些网络的度分布很好的近似于一个幂律分布。
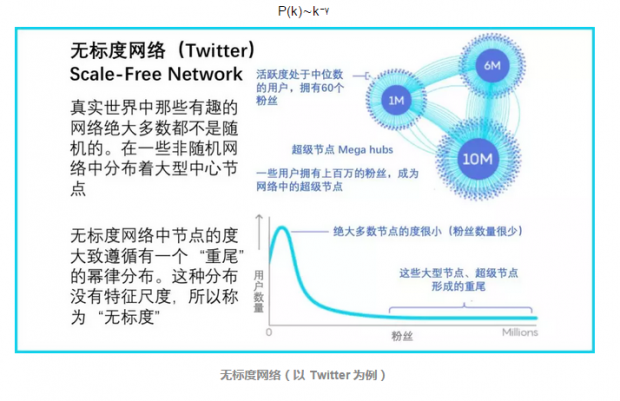
这是一个意外的发现,因为当时主流的是 Erdős 和 Rényi 提出的随机网络,随机网络满足泊松分布,有明显的特征尺度,例如。而幂律分布则没有。于是我们将这些网络命名为无标度网络,其灵感来源于相变周围观察到的幂律的无标度性质。
3.无标度网络
是一种解释幂律现象的机制模型
机制模型。1999年,Réka Albert 和我研究了网络中节点度分布的幂律现象,发现幂律源于生长模型和偏好依附这两种机制。基于这两个机制,我们提出了一个简单的模型,解释网络中幂律的起源,就是今天大家熟知的无标度网络模型。根据无标度网络模型生成的网络,度分布均满足幂律指数为3。
无标度模型是一个机制模型,也就是说它不是描述互联网、WWW或者细胞网络的模型。它只是用来解释一个网络的无标度特性背后的机制。真实世界的网络比理论模型复杂得多,真实网络的幂指数,数值从2到8不等,而无标度网络的幂指数则不会超过3。单靠生长模型或者偏好依附两种机制,并不能解释幂指数的大幅跳跃。
4.真实世界的网络是怎样的
真实网络。1999年文章发表之后的几个月,一些关键的发现也帮助了大家理解系数不同的原因。由 Mendes, Dorogovtsev, Redner, Krapivsky 等人发现的基于连续理论的速率方程,将发生在真实网络中的许多因素纳入到了无标度模型中,比如节点的消失,新连接的建立,旧连接的删除,连接老化等等。这些现象在真实网络中很常见。
一系列的研究表明,这些额外因素的存在以两种方式改变网络的度分布。
首先,这些因素直接改变了幂指数,这也成功的解释了真实网络的指数的不同。
另外,这些因素促进了对度分布的修正,使得P(k)以可预见的方式偏离单纯的幂律。常见的修正包括:
-
小度饱和:在任意的系统中,网络中已经存在的两个节点可以选择互相连接(内部连接),它们的度分布的分析形式可以写成P(k)=C(k+A)⁻ᵞ,就会产生小度饱和。在社交网络和WWW中,很多连接都是这样的内部连接。类似的小度饱和也可以由最初的吸引产生,这在引文网中有记载[8]。
-
高度截断:如果偏好依附是非线性的,那么度分布就会遵循拉伸指数,或者具有指数截断的幂律。移除节点也会产生类似的高度截断。
-
适应度:在连接中,节点有不同的能力,这种多样性的建模可以通过给每一个节点一个独特且不同的适应度η。有了适应度之后,P(k)的精确形式将会基于适应度的分布ρ(η)。比如一个均匀的适应度分布将会使P(k)有一个log修正,而其他形式的ρ(η)也可以导致P(k)更奇特的形式。
5.真实网络中,
无标度特性不会单独出现
在真实世界中,上述过程常常会一起出现,所以实际的网络会很复杂。
早在2001年,我们就很清楚:对于由无标度机制生成的网络,它们的度分布无法用一个万能公式来解释。单纯的幂律只出现在简单的理想化的模型中,仅仅由生长机制和偏好依附驱动,并并且不受其他因素干扰。
上述理论表明,在真实网络中如果出现了无标度性质,那么幂律往往会和一些修正方程同时出现,比如幂律会带有高度截断、指数拉伸或者幂律的log修正等等。
这些理论非常重要,因此我在《网络科学》一书中用一整个章节阐述。

有多种方式分析无标度性质的方法,我在附录Box1《如何分析真实网络》中做了介绍。结论简单,也容易理解:如果我们希望得到一个真实网络的精确的度分布的拟合,我们首先必须建立一个生成模型可以分析预测P(k)的方程形式。
✎Box1: 我们如何分析真实网络?
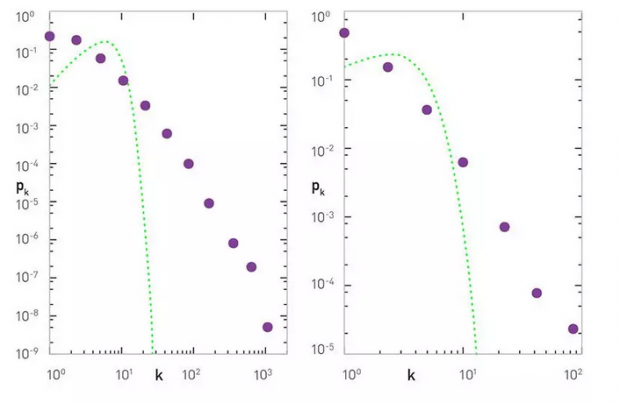
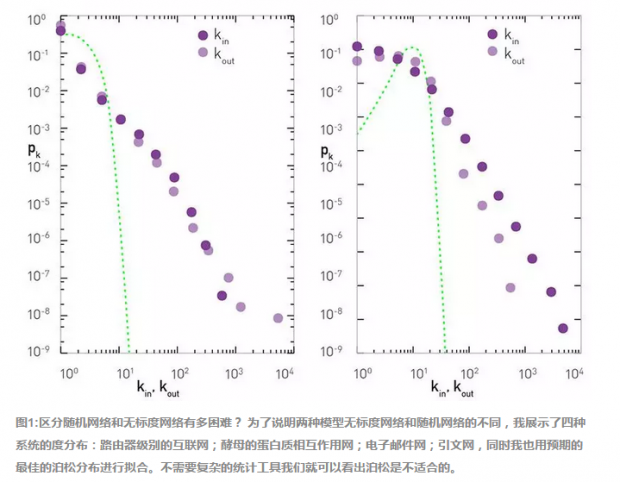
由于真实系统的复杂性,我们如何检测真实网络的无标度性呢? 我们可以比盲目地进行幂律拟合做的更好。当然,我们选择的方法取决于我们想要解决的问题:
如果我们的目标是对度分布进行准确的拟合,那么我们必须对我们要拟合的网络建立一个连续模型。这种做法已经在几个被充分研究过的系统中成功完成,并且发现在每一种情况下,通过生长机制和偏好依附得到的无标度机制对描述网络的拓扑结构是非常必要的。
如果我们的目标是获得无标度机制的直接证据,那么我们不需要努力完成1中的工作就可以做到这一点,但前提是我们有动态数据(比如添加每个节点或连接的时间)。在这种情况下,我们可以直接同时评估生长机制和偏好依附[10]。
最后,如果我们想要看到的是无标度性的结果,我们可以绕过1和2并且度量度分布的方差。这会引起我们的问题,为什么无标度性这么重要?我将会在Box2中讨论,我还会展示如何通过度量度分布的方差来检测无标度性的影响。
✎Box2: 为什么无标度网络很重要?
为什么无标度性在过去二十年得到那么多的关注? 主要原因是无标度性真的很重要。实际上,Cohen, Havlin, Pastor-Satorras, Vespignani和其他人在 [11]的突破性发现表明有很高的的网络有一系列不平常的性质,比如故障的鲁棒性,攻击的脆弱性,病毒异常传播,异常同步等等。对于具有单纯幂律度分布的无标度网络,当γ<3时, ⟨k²⟩ 发散,因此它们显示出这些有趣的特性。另外,你并不需要一个单纯的幂律来见证高 ⟨k²⟩ 的影响,因为由无标度机制驱动的系统往往具有异常高的⟨k²⟩。您可以通过比较真实网络的方差与类似大小的随机网络的方差来轻松的进行测试(请参见图2)。如果值很高,那么无标度模型的有趣特性将在你的网络中体现出来,无论度分布是否遵循单纯的幂律。
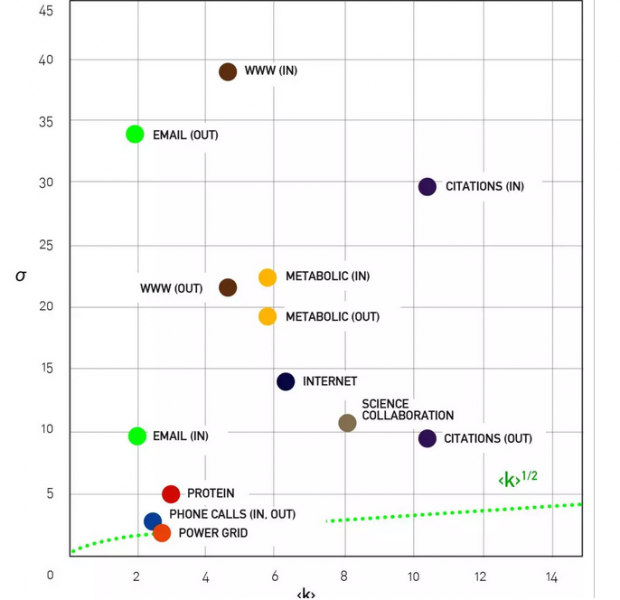
实际网络中度的高方差特性。对于具有泊松度分布的随机网络,度数的标准偏差如图中绿色虚线所示。 符号σ代表九个参考网络。对于每个网络,σ大于具有相同的随机网络的预期值。 唯一的例外是电网,它不是无标度的。 虽然通话网络是无标度的,但它具有很大的γ,因此它可以很好地被随机网络近似。
6.《无标度网络很罕见》
文章的矛盾之处
现在让我们回到 BC 文章以及它的关键声明“无标度网络是罕见的”。它到底是怎样得到这样的结论的呢?
非要对每一个网络进行一个单纯的幂律拟合,并且忽略理论对网络的预测,那么自然就会得到很罕见的结论。因为很难找到没有额外效果的真实系统,因此对所有的真实系统进行无差别的幂律拟合是毫无道理的。正确的做法应该是拟合出可以用理论预测的分布,并且每一个系统的分布都应该是不同的。
有趣的是,理论预测在很多由生长机制和偏好依附驱动的真实网络中,度分布应该满足带有指数截断的幂律。然而如果你看BC文章中的表2,BC发现51%的网络支持这种分布。换句话说,BC 文章的作者验证这个理论的方式,与作者的中心思想是矛盾的。

技术问题
7.大量研究发现
无标度特性的确广泛存在
了解真实网络的特点后,你可能会问,如果度分布是很难拟合的,那么为什么上千篇文章会表明大量的真实网络,从互联网到蛋白质相互作用网再到社交网络,都是无标度的呢?
答案很简单,对于许多真实网络来说,尽管很多过程都参与塑造了它们的拓扑结构,但是它们的肥尾(fat tail)性质非常明显,难以忽视。
实际上,在作者 Clauset 被引用最多的一项工作中,也考虑到了互联网,蛋白质相互作用网,引文网,科学家合作网等大型网络的无标度特性,而且连必要的修正都没有做。见[12]中的表6。
8.技术问题之一:
作者没有严肃地设置评判标准
所以在技术上最让人疑惑的问题是:为什么在这篇论文中作者没有发现网络的无标度性,而在其他许多文献中都有,甚至连作者 Clauset 自己早期的工作中也有?
这里就出现了第一个技术上的奇怪地方:他们之所以没有发现无标度性质,是因为他们发明了一种评价强弱无标度网络的新标准。
不仅如此,真正令人惊奇的是,就连那些由无标度模型生成的完全遵循幂律分布的网络,也不能通过他们的测试。多么不可思议。证据就在其论文的附录 E 中。现在让我们来探究一下。
你可能认为 BC 文章所谓的“弱”、“强”无标度网络,一定具有统计显著性。这是常识了,如果人们把那些大而精确映射的真实网络称为“强无标度网络”,就意味着它们在统计显著性上很明显。同样,“弱无标度网络”意味着在这个网络中,幂律的统计显著性不明显。
然而这并不是 BC 文章的观点。他们的方案是,采用每一个网络,并且从原来的多个合成网络模型生成网络。这样,927个真实网络数据集变成了23999个合成网络,然后他们直接刨除了81%的网络,认为它们“不可能是无标度的”(BC 文章第3页)。他们真正研究的是剩下的4477个合成网络。
9.以引文网络为例
证明其评判标准的荒谬性
举个例子,一个无权有向网比如WWW,变成三个不同的度序列:入度,出度和总的度。他们不问这些合成网络中的哪一个可能符合幂律,而是问这些合成网络的哪部分通过了幂律的标准。然后他们提出了接下来这些命名标准,我列出来摘自他们的文章的这些判断:
-
超弱(Super-weak):至少50%的网络,除了幂律以外的任何一种其它分布都不符合。
-
最弱(Weakest):至少50%的网络,幂律假设不会被拒绝(p>=0.1)。
-
弱(Weak):满足最弱集合的要求,并且在分布的尾部至少有50个节点(ntail > 50)。
-
强(Strong):满足弱集合的要求,2 < αˆ < 3,并且对于至少50%的网络,更符合幂律分布而不是其他分布。
-
最强(Strongest):要求至少90%的网络满足强集合的要求,而不是50%,并且至少95%的网络,更符合幂律分布而不是其他分布。
为了更好的理解这些,让我们以已经被充分验证过是无标度网络的引文网为例。引文网是有向网,它的入度(一篇文章所引用的文章的数量)从20世纪60年代就被认为是符合幂律的[13]。
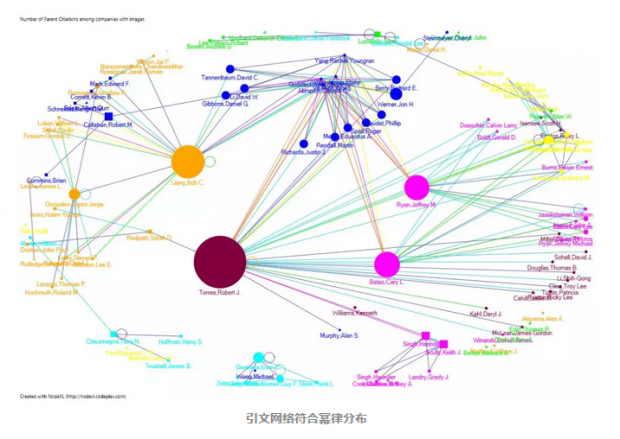
然而,出度满足一个不同的分布,因为这些度捕捉一篇文章被多少不同的文章引用,并且这个数值会由杂志的政策决定,有人工截断的因素在里边。
因此,由这样一个被很好的研究过的无标度网络生成的三个网络,只有一个能通过BC他们的标准,也就是由入度定义的那个网络。但是按照BC的说法,这样的网络甚至不是超弱的无标度网络。
在某些情况下,他们的方法可以用真实网络生成多达900个合成网络。如果这些合成网络中至少有50%通过幂律测试,他们会认为它超弱。他们要求90%通过才能将网络置于最强的分类中。
事实上,这些网络中通常只有一个很重要:捕获原始系统的目的或功能的网络。但是他们认为每个虚构的合成网络都具有平等的投票权,让它们共同来决定原始系统是否是无标度的(Box 3)。
✎Box3:“All you need is love”
如果读者很难理解进行超弱,最弱,最弱,最强和最强分类的要求,那么,你要知道你不是唯一的一个。 我花了几天才明白,所以让我简单地解释一下。
假设我们想要在以下字符串中找到“Love”这个词:“Love”。 当然,你可以简单地匹配字符串,并称其完成了任务。 然而,这无法给你的匹配提供统计意义。
BC坚持认为我们必须使用严格的算法来判断“Love”是否存在于“Love”里。 然后他们就提出一个算法,算法是这样工作的:取原始字符串,并将其分解成所有可能的子字符串:
{L,o,v,e,Lo,Lv,Le,ov,oe,ve,Lov,Loe,ove,Love}.
如果这些子串中至少90%与Love相匹配,他们称该匹配为超强。 在这种情况下,我们确实在列表中有Love,但它只是14个可能子字符串中的一个,所以Love不是超强的。
如果至少有50%的字符串与搜索字符串匹配,他们称该匹配超弱。 Love显然不是超弱的。
最后,Clauset的算法达到了不可避免的结论:Love里没有Love。
那么我们其它的人呢?你需要Love。
BC 文章的分类方法在网络科学中并没有先例,并且与他们研究的网络特性也无关。另外,它们并没有解释这些标准制定的必要性,也没有解释他们是如何选择50%和90%的百分比的。 这些都是任意的。
10.技术问题之二:
无标度网络就是无标度网络,
不是别的
但是让我们关注真正重要的事情:控制。也就是说,无论我们选择什么标准,都必须在度分布可以被很好理解的网络上进行测试。
因此好的测试方法是,由无标度模型生成一个符合幂律分布的、未经任何修正的无标度网络,把这样的网络用我们的方法检测,应该可以判断出该网络属于无标度特性最强的类别。
实际上,如果这样满足“黄金标准”的网络不能归为“最强”的类别,那么还有什么网络是“最强”呢? 换句话说,无标度模型应该能够成为超弱、最弱、弱、强、最强这些类别里“最强”的那个,难道不是吗?毕竟我们对无标度模型的幂律性质有正式的确切的证据[14]。
BC 事实上意识到了这个关键的标准,因此他们在第5页向读者保证,他们的方法通过了这个明显而又重要的测试:
用两种机制产生了无标度网络(一种直接使用偏好依附[42]和一种直接节点复制模型[43]),另外生成了不具有无标度性质的网络(简单的ER随机网)。将我们的方法应用在这些机制生成的合成网络上,我们正确的将合成数据集分类成适合它们的生成参数的无标度分类中,比如,偏好依附和节点复制的数据集被分类到无标度网络中,而ER随机网并没有(见Appendix E)。
很好。然而很奇怪,我读了论文的附录 E,觉得这里应该简单提供一些证据。它确实这样做了。但是,它给的并不是我们期望的基于上述内容的证据。
当我们考虑幂律拟合的合理性时,我们只能看到很少的网络符合。62%的偏好依附的网络被分在最弱和弱的类别里。
11.不能正确区分随机网络
和无标度网络的“黄金标准”
BC 文章也提到ER随机网络,“分别有51%和50%的网络被分在了最弱和弱的类别”。
换句话说,通过作者发明的标准,38%的无标度网络连“弱无标度”都算不上。但是,51%的ER随机网却被归类为“弱无标度”。
你可能会问,区分ER模型和无标度模型到底有多难?在BC 的测试中,他们使用了有5000个节点的网络。在图3中,我们可以看到在这个尺度下的无标度网和ER网的度分布的是多么的不同。它根本不需要复杂的统计测试来捕捉这些差异。
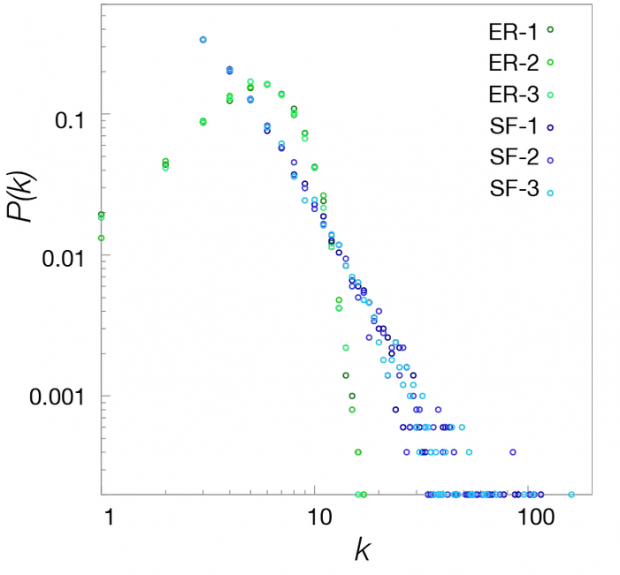
图3: 区分不同 ER随机网模型和无标度模型
我们对于BC采用的方法无法区分ER和无标度模型的原因很好奇,因此我们也为节点数N=5000的两个模型生成了度分布,与BC用于测试的网络大小相同。我们实现了 BC 文章附录E中描述的无标度模型,这是原始无标度模型的一个版本(他们的选择有问题,但是我们现在不要详述)。
在该图中,我们为每个网络显示了三种不同的实现,我们能够看到不同实现之间的差异,尽管在这种规模下差异很小。但是这两种模型之间的差异是不可忽略的:任何ER网络中的最大节点的度都小于20,而无标度模型则会生成具有数百个连接的中心节点。即使是一个构造不好的统计测试也可以说明差异。然而,BC 使用的方法中有38%的无标度模型没有被归为“无标度”,而51%的ER模型被归类为“无标度”。
另一点也很有趣。如果我们读一下BC文章第7页的内容,就会看到他们制定的无标度网络黄金标准。(他们把无标度网络称为偏好依附网络):
当我们考虑幂律拟合的合理性时,我们只能看到很少的网络符合。62%的偏好依附网络被分在最弱和弱的类别里,60%在强类别中,而0个在最强类别中。
也就是说,没有一个单一的无标度模型被认为是具有很强的无标度性质的。 根据他们发明的标准,无标度模型甚至也不再是无标度的。
12.BC 文章的方法失误,
结论夸张
预印本论文的主要结果在报刊上突出说法:作者未能在自然界找到大量的无标度网络。但如果我们真的读了这篇论文就会发现,其实是他们拒绝看到这样的结果:BC 论文中的表2已经显示,很大一部分的网络的度分布都与描述无标度网络的连续统计理论的预测一致。
真正的失败之处是他们的方法:没有证明这套黄金标准是无标度的。现在,如果你发明了的一个任意的标准,甚至连数学证明的模型都不能通过,你还期望得到什么?
经过上面的分析,真正让我迷惑的是,4%的真实网络通过了他们的标准,被认为是强无标度的。哪些网络是比无标度模型更加无标度的呢?简直像做梦一样!
13.结语:
无标度网络理论依然可靠
对于网络科学而言,不断测试其基础理论的可靠性是很重要的,比如真实网络的无标度性质,以及其背后的机制。因此,我们必须继续不断排除竞争性假设,这是科学进步必不可少的过程。但是,偷工减料的研究并不能让科学进步。
所以,在接受这篇论文的引人注目的结论“无标度网络其实很罕见”之前,你必须仔细阅读它。并且,如果你花时间读了,你会发现这项研究忽略了网络科学已经积累18年的知识。你还可以找到一个对于无标度网络的虚构的标准。
最重要的是,你还会发现他们的无标度的黄金标准并没有通过最基本的测试。这些都是大问题。如果你愿意投入时间,你还会发现额外的技术失误。
这场争议必须结束。对于无标度网络理论,还没有出现颠覆现有范式的严肃研究。
附录
✎Box4: 几片羽毛改变不了万有引力
任何修过力学课程的人都可能熟悉BC遇到的情况。教科书告诉我们,根据牛顿的重力理论,下落物体将随着g而加速。但是,如果我从网络科学研究所11楼的窗户上自由落体一块岩石和一根羽毛,并测量它们的加速度,我很快就会得出结论,牛顿定理是有缺陷的。首先,我只会观察短时间的加速度,加速度会小于g。 其次,在这个初始阶段之后,岩石和羽毛都会以不变的速度下降。这两个观察都违反了牛顿定理。 但是,如果我会得出这样的结论:重力是错误的,那我将会放弃我的力学课程。而能让我通过的正确答案,就是承认下落物体的轨迹受重力和摩擦的影响。 一旦将摩擦添加到等式中,我将能够得到羽毛和岩石的完整轨迹。
14.参考文献
[1] AD Broido, A Clauset. Scale-free networks are rare. arXiv:1801.03400
[2] A.-L. Barabási and R. Albert. Emergence of scaling in random networks. Science, 286:509-512, 1999.
[3] R. Kumar, P. Raghavan, S. Rajalopagan, and A.Tomkins. Extracting Large-Scale Knowledge Bases from the Web. Proceedings of the 25thVLDBConference, Edinburgh,Scotland,pp.639-650,1999; H. Jeong, R. Albert and A. L. Barabási. Internet: Diameter of the world-wide web. Nature, 401:130-131, 1999;
[4] M. Faloutsos, P. Faloutsos, and C. Faloutsos. On power-law relationships of the internet topology. Proceedings of SIGCOMM. Comput. Commun. Rev. 29: 251-262, 1999.
[5] P. Erdős and A. Rényi. On random graphs, I. Publicationes Mathematicae (Debrecen), 6:290-297, 1959.
[6] P. L. Krapivsky, S. Redner, and F. Leyvraz, Connectivity of Growing Random Networks”, Phys. Rev. Lett. 85, 4629-4632 (2000); S.N. Dorogovtsev, J.F.F. Mendes, and A.N. Samukhin. Structure of growing networks with preferential linking, Physical Review Letters, 85: 4633, 2000.
[7] For more details, see Chapter 6 of Network Science.
[8] Y.-H. Eom and S. Fortunato. Characterizing and Modeling Citation Dynamics. PLoS ONE, 6: e24926, 2011.
[9] A.-L. Barabási Network Science. Cambridge University Press, 2017.
[10] Section 5.7 in Ref. [9].
[11] R. Cohen, K. Erez, D. ben-Avraham and S. Havlin. Resilience of the Internet to random breakdowns. Physical Review Letters, 85:4626, 2000; B. Bollobás and O. Riordan. Robustness and Vulnerability of ScaleFree Random Graphs. Internet Mathematics, 1, 2003; R. Pastor-Satorras and A.Vespignani. Epidemic spreading in scalefree networks. Physical Review Letters, 86:3200–3203, 2001.; R. Albert, H. Jeong, A.-L. Barabási. Error and attack tolerance of complex networks. Nature, 406: 378–482, 2000;
[12] A Clauset, CR Shalizi, MEJ Newman. Power-law distributions in empirical data. SIAM review 51 (4), 661-703, 5933 (2009).
[13] In some cases, depending how the data was collected, the log-normal also offers a reasonable fit to citation networks. For the power law, we have generative methods; the mechanistic origin of the log normal are less understood.
[14] B. Bollobás, O. Riordan, J. Spencer, and G. Tusnády. The degree sequence of a scale-free random graph process. Random Structures and Algorithms, 18:279-290, 2001.
[15] R. Cohen, K. Erez, D. ben-Avraham and S. Havlin. Resilience of the Internet to random breakdowns. Physical Review Letters, 85:4626, 2000; B. Bollobás and O. Riordan. Robustness and Vulnerability of ScaleFree Random Graphs. Internet Mathematics, 1, 2003; R. Pastor-Satorras and A.Vespignani. Epidemic spreading in scalefree networks. Physical Review Letters, 86:3200–3203, 2001.; R. Albert, H. Jeong, A.-L. Barabási. Error and attack tolerance of complex networks. Nature, 406: 378–482, 2000;
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 