文 | 张江

导语：随着共享出行的普及，以及全路网的自动驾驶变得越来越可能，我们完全可以实现一个由算法管理的乌托邦式的城市交通系统。这样的系统可以做到按需交通（On-demand urban mobility），即根据每个人的需求动态地分配运载车辆，从而实现整体的最优化。从技术上说，作者首先把按需交通问题映射为一个理想化数学问题——最小车队问题，并在与实际纽约市出租汽车15亿条出行数据相结合的情况下，给出了该问题的最优解。结果表明，使用算法管理的交通系统可以将出租车使用数量减少40%左右。即使在考虑到出行需求可能实时提交处理的情况，这一缩减量也可以达到30%。因此，该问题的解决不仅可以大大提升共享出行系统的运行效率，也为未来人工智能治理的社会模式提供了一个非常好的示范案例。

 

自动驾驶与车联网，以及共享出行模式这三种大的趋势将会彻底变革我们未来的交通系统与出行模式，这使得整个交通系统都可能都统一被算法所管理。因此，一个“乌托邦式”的交通系统将不再遥远，在其中，算法可以调度每一部车辆，从而让系统在整体的运行效率达到最高，并能最大化地实现绿色环保。这种模式将会大大优于现有的交通模式，私家车、出租车、公交车将有可能成为历史。

 

要实现这样的“乌托邦式”交通系统，算法是其中最重要的一环。因为，为了满足所有市民的出行需求，我们需要合理地调度每一部奔跑在道路网络上的自动驾驶汽车，从而做到：（1）能够尽可能高效地满足每一位市民的出行需求；（2）能够在整体上达到成本最小，也就是用最少的车辆和交通来实现尽可能多的出行需求。这样的算法存在吗？一个来自MIT、意大利比萨信息与通信技术研究院以及康奈尔大学、康奈尔技术的合作研究团队给出了肯定的回答。

 

 

1.最小车队问题

 

该合作团队首先将人们的出行需求简化成了一道并不简单的数学题。让我们来考虑A、B、C、D、E、F这六个人的出行需求，如图1所示：

 

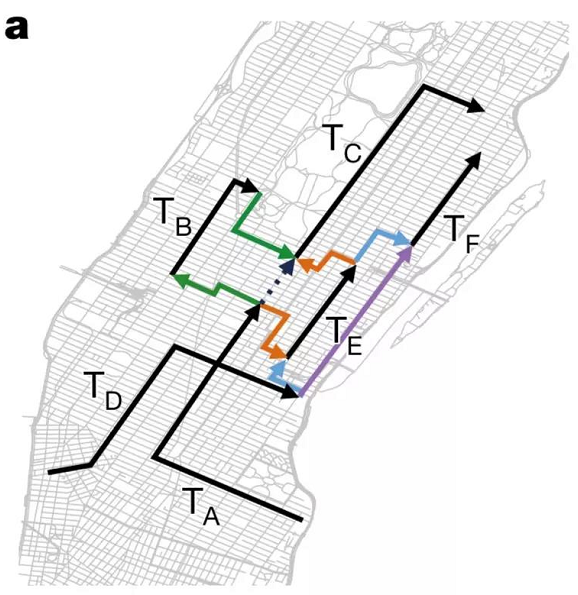
图1：ABCDEF六个人的出行轨迹示意图，分别用T_A、T_B……T_F来表示

 

T_A、T_B、……、T_F这每一段折线都代表一个用户的出行需求，即用户要从时间点t_p，和地点l_p出发，并在时间t_d到达地点l_d。其中，t_p是自动驾驶汽车能够接到用户A的最早时间，而t_d时间点则可以根据出发时间t_p和路网情况（交通流等因素）估计出来的时间点。

 

假设，我们可以调度一组自动驾驶车队来满足这一组用户的出行需求。于是，我们可以给每一条出行路线分配不同的汽车，也可以让同一辆汽车先后满足两个用户的出行需求，只需要第二个用户的出行需求与上一个用户的完成时间和空间都相隔不太远就可以完成。也就是说，一辆自动驾驶汽车在完成了一个用户的任务之后，还可以继续接另一个用户，只要该用户所产生的需求时间t_p与该自动驾驶汽车完成上一个任务的结束时间t_d，并考虑到自动驾驶汽车从上一个l_d开到下一个l_p之间的时间间隔不算太大就可以了。

 

在图1中，彩色的折线段就是一辆自动驾驶汽车在完成了上一个任务之后，进一步完成下一个任务的转换路径。例如，当自动驾驶汽车接到A，并完成任务后，就可能沿着绿色箭头走到B的出发点把B接上送到B的目的地，然后又可以顺着绿色折线箭头赶到C的出发点，从而满足C的需求。

 

当然，这辆接送A的自动驾驶汽车也可以在载完A后沿着橙色箭头走到E的出发点，然后又去接C，……。因此，在一组给定的用户出行的地点、时间和目的地的情况下，我们的自动驾驶汽车车队可以有不同的方式来满足尽可能多的出行需求。

 

那么，所谓的最小车队问题也就是：在一组给定的出行需求情况下，我们能否用最少的自动驾驶汽车数量来服务所有的出行任务？

 

可以想到，如果我们能够从数学上解决这个问题，那么我们就可以用一种最“经济”的方式来运作我们的自动驾驶交通系统，从而做到节约能源、绿色环保。

 

2.车辆共享网络

 

然而，这样的抽象问题一下子很难解决，我们必需一个中间过渡工具，这就是“车辆共享网络”（Vehicle-shareability network）。这一网络模型是在参考文献[7]中提出的一种描述共享交通模式的网络模型。他可以用来建模不同的车辆分配方案。例如，图2的有向网络就是一个车辆共享网络，它建模了图1所对应的不同的车辆分配方案：

 

 

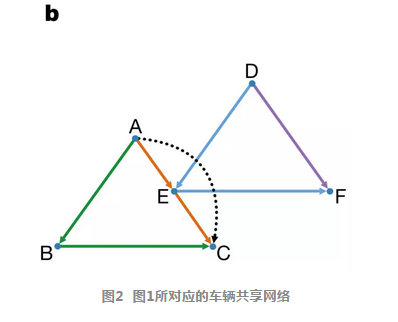
在图2这张网络中，一个节点就对应了图1的一个用户的出行需求，因此A就对应图1中T_A这条出行路径。而该图中的一条有向连边则对应了一种可能的任务切换，换句话说，如果节点A和B之间有连边就表示自动驾驶汽车有可能在完成了A任务之后再去完成B任务；如果没有链接，就表示自动驾驶汽车可能在完成了A任务之后由于时间间隔太长，或空间距离太远而不可能再去完成任务B。

 

图1中的可能路径切换都对应到了图2中的有向连边中。其中，某一辆汽车的完成任务方案就对应为图2中的一条同颜色的有向路径。例如图2中的绿色路径则对应了陆续接送了A、B、C三个用户的自动驾驶汽车。

 

要想满足所有人的出行需求，就是要寻找到一组路径划分方案，从而使得这些路径能够覆盖共享出行网络上的所有点（服务所有出行需求）。很显然，这样的路径划分方案有很多种，那么什么是最优的呢？

 

非常有趣的是，这一最少覆盖路径问题恰好就是前文叙述的最小车队问题。于是，利用车辆共享网络，我们巧妙地将最小车队问题转化为了共享网络上的最少路径覆盖问题。

 

总结来看，我们可以从实际数据出发，利用车辆共享网络来构造一个“最少路径覆盖问题”，它的步骤如下：

 

 

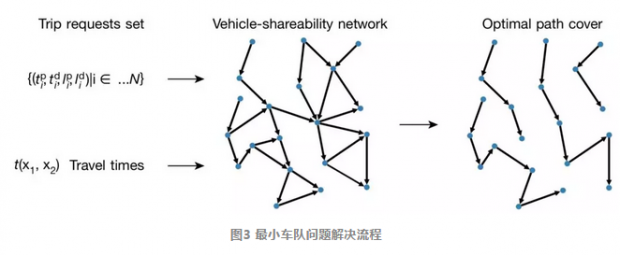
接下来，这个问题怎么求解呢？坏消息是，对于一般意义上的最优路径覆盖问题来说，这是一个NP难的问题，我们无法找到有效的计算求解方案；但好消息是，由于我们这个交通工具共享网络具有特殊性，即它是一个有向无环图（directed acycled graph）。这也就意味着，我们可以使用Hopcroft-Karp算法找到该问题的有效解法（具体参见论文附录）。

 

3.“乌托邦交通”的运行效果

 

接下来，就让我们来看看这样的最优共享方案的效果如何。作者们结合了纽约市2011年所有出租车的出行数据来构建车辆共享网络。这套数据集中包含了15亿条出行记录，每一条出行记录都对应了用户被出租车接上的时间，也就是t_p、地点，也就是l_p，以及在什么时间，即t_d，用户被送达到指定地点，也就是l_d。这样，我们就可以套用图3所示的算法流程，来计算出每一天，甚至每一小时最优的出租车数量，并与实际出租车使用数量进行对比。

 

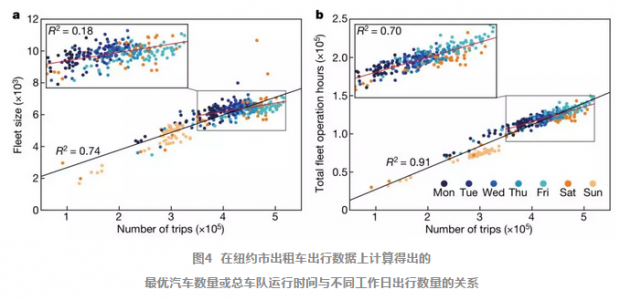
首先，如图4所示，我们看到最优的出租车使用数量是会随着人们出行需求的增加而线性增加的。其中不同颜色的点表示不同的工作日（周一、周二等）。右侧的图则展示了车队运行的总时间随着出行次数的增加而线性增加。而我们看到，当出行量在从300,000到550,000之间的时候，增长的斜率会小一些，这表明不仅仅是出行密度，人们出行的模式也会影响最优的数量。

 

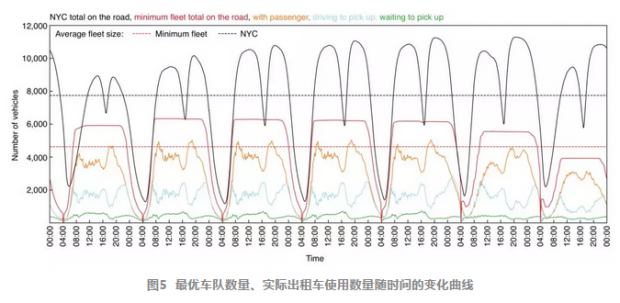
其次，图5展示了实际出租车使用数量（黑色）、最优出租车使用数量（红色），以及处于不同模式的出行出租车数量（其它颜色）随时间的波动曲线。虚线对应的是它们的平均值。我们看到，如果使用算法来管理整个交通系统的话，我们每天平均仅需要实际出租车数量的60%就可以了，这足足减少了3000辆出租车的使用！

 

4.更现实的考虑

 

虽然60%这个数字是相当惊人的，但是这个数字是建立在一天内所有的需求都是同时提交给优化系统的假设前提下的，这样系统能够有条不紊地安排所有车辆的出行，从而最优化出行配置。

 

然而，现实情况会比这种情况更加“骨感”得多：一天内的出行需求不可能一下子同时提交给我们的服务器，而必然是实时地、一个个地提交给系统的。那么在这种情况下，我们就需要改进算法。于是，作者提供了两种改进，分别叫直接（on-the-fly）算法和批次算法（batch）。

 

在第一个算法中，出行需求是序列地一个个被处理的。系统会在所有的车辆中自动选择一个能够让用户等待时间最短的车辆来服务。

 

在批次算法中，系统是每间隔δ = 1分钟，收集一个批次的需求数据，并利用最大匹配算法来满足所有用户，并让等待时间最短。

 

为了对比这两种算法，我们使用比最小车队问题略大的车辆数（N_{min}x,其中N_{min}是最小车队数量，x是一个略大于1的参数）来运作，并通过比较两个不同算法的服务总需求的百分比作为评测的指标，结果如图所示：

 

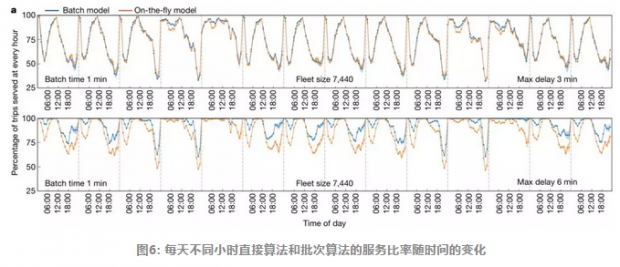
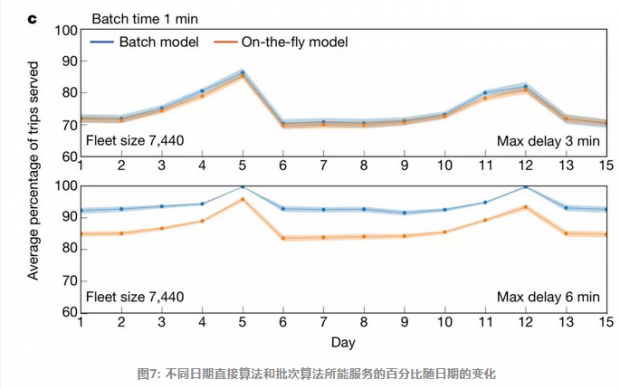
图6、7中的横坐标是时间，纵坐标是算法服务的出行百分比，这个百分比越高说明算法越好。我们看到，无论是从小时为单位衡量的出行还是以天为单位的出行，批模型的服务百分比更高。

 

通过结合出行实际数据和优化算法，我们发现，使用批次模型，我们可以使用实际数量70%的出租车来服务超过90%的出行需求。这虽然没有最优模型酷炫，但也说明考虑到实时服务的情况下，我们仍然可以做到尽可能的高效和足够多用户的满意。

 

5.人工智能社会的未来

 

最后，作者总结道：虽然这套算法仅仅解决了单一出行模式、单一车队的优化问题，但它完全可以扩展到多种出行模式的混合交通的优化问题，这为我们解决出行问题提供了更多的想象空间。尽管更便捷的出行很有可能刺激人们更多的出行需求，但是总体来讲，由高效算法管理的自动驾驶交通系统将必然会让我们的交通更加高效和智能。

 

笔者甚至认为，这篇工作的意义可能还可以延伸到更多的共享经济模式中。利用算法而非人类的主观决策来统一调配管理整个宏观系统将在未来成为可能。

 

参考文献：

[7] Santi, P. et al. Quantifying the benefits of vehicle pooling with shareability networks. Proc. Natl Acad. Sci. USA 111, 13290–13294 (2014). 

论文下载：

链接：https://pan.baidu.com/s/1weycQSRQISv8xEl1cgtkkg  密码:0zpw