在量子计算机研究的早期，计算机科学家提出了一个问题，他们知道这个问题的答案将揭示这些未来机器的能力。 二十五年后，它终于快要被解决。 在5月底在线发表的一篇论文中，计算机科学家Ran Raz和Avishay Tal提供了强有力的证据证明量子计算机具有超越经典计算机所能达到的计算能力。

论文传送门：

https://eccc.weizmann.ac.il/report/2018/107/

Raz是普林斯顿大学和魏茨曼科学研究所的教授，Tal是斯坦福大学的博士后研究员，他们定义了一种特定的计算问题。在特定的条件下，他们证明量子计算机可以有效地处理这个问题，而经典的计算机在试图解决它时将永远陷入困境。自1993年以来，计算机科学家一直在寻找这样一个问题，当时他们首先定义了一类被称为“BQP”（bounded-error quantum polynomial time）的问题，它包括量子计算机可以解决的所有问题。

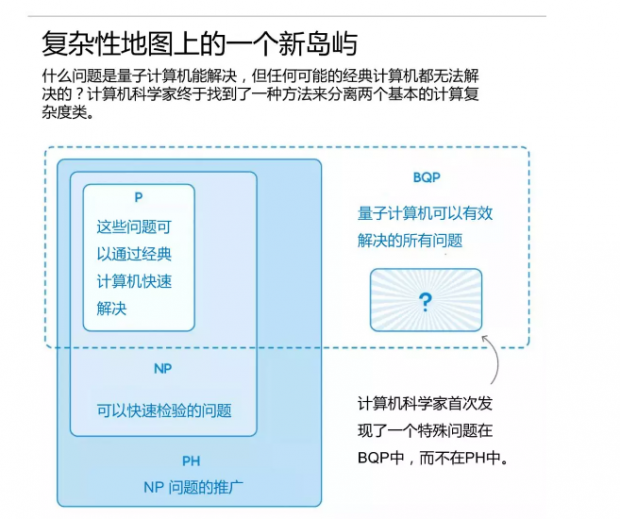
从那以后，计算机科学家们希望将BQP与一类被称为“PH”（polynomial hierarchy）的问题进行对比，“PH”包括任何可能的经典计算机都可以解决的所有问题 - 甚至是由未来文明设计的不可思议的先进计算机。做出这种对比取决于找到一个可以证明在BQP中而不是在PH中的问题。而现在，Raz和Tal已经做到了。

他们的结果并不是说量子计算机将在所有实际情况中超越经典计算机。一方面，理论计算机科学家已经知道量子计算机可以解决经典计算机可以解决的任何问题，然而工程师们仍在努力建造一个实用的量子机器。但Raz和Tal的论文表明量子和经典计算机确实处在不同的类别 ——即使经典计算机能成功解决所有它可能解决的问题（P等于NP，PH坍缩），量子计算机仍将超越它们。

理论计算机科学的基本任务是将问题按复杂度来分类。复杂度类包含在给定资源内可解决所有问题，其中资源类似于时间或内存。

计算机科学家已经找到了一种有效的算法，例如，用于测试数字是否为素数。 但是，他们还没有找到一种有效的算法来找出大数的素数因子。因此，计算机科学家相信（但未能证明）这两个问题属于不同的复杂度类。

两个最著名的复杂度类是“P”和“NP”。P是经典计算机可以快速解决的所有问题。（“这个数字是素数吗？”这个问题属于P）。NP是经典计算机不一定能够快速解决的所有问题，但是如果提出答案，他们可以快速验证答案。 （“它的素数因子是什么？”属于NP）。计算机科学家认为P和NP是不同的类别，但实际上证明P不等于NP是该领域中最难和最重要的开放问题。





1993年，计算机科学家Ethan Bernstein和Umesh Vazirani为“有界误差量子多项式时间”（bounded-error quantum polynomial time）定义了一个他们称之为BQP的新复杂度类。他们将这个类别定义为量子计算机可以有效解决的所有决策问题 - 答案是“是”或“否”的问题。大约在同一时间，他们也证明了量子计算机可以解决经典计算机可以解决的所有问题。也就是说，BQP包含P中的所有问题。

注解1. 在考虑复杂度类时，示例会有所帮助。 “旅行推销员问题”中所说的是否有一条通过诸多城市的路径比某个给定距离短，它属于NP。一个更复杂的问题是，通过这些城市的最短路径是否恰好等于那个距离，这个问题属于PH。

但是他们无法确定BQP是否包含这样一个问题，这个问题不被包含在另一个称为“PH”的重要类别中。PH代表“多项式层次结构“（polynomial hierarchy），是NP的推广。这意味着从NP中的问题出发，逐层加入像“存在”和“对于所有情况”这样的限定语句使其变得更加复杂时，PH包含了所有你会遇到的问题。今天的经典计算机无法解决PH中的大多数问题，但是你可以把PH看作经典计算机可以解决的所有问题的类，如果最终发现P等于NP。 换句话说，比较BQP和PH是为了确定量子计算机是否具有优于经典计算机的优势，即使经典计算机能够（意外地）解决比现在更多的问题。

“PH是最基本的经典复杂度类之一，”德克萨斯大学奥斯汀分校的计算机科学家Scott Aaronson说。 “所以我们想知道，量子计算在经典复杂性理论领域中处于什么样的地位？”

区分两个复杂度类的最佳方法是找到一个可被证明属于一个而不属于另一个中的问题。 然而，由于基本原理和技术结合的障碍，找到这样的问题一直是一个挑战。

如果你想要一个属于BQP而不属于PH的问题，你必须明确该问题 “按照定义，经典计算机甚至无法有效地验证答案，更不用说找到它了，” Aaronson说， “这排除了我们在计算机科学中考虑的很多问题。”

这是问题所在。想象一下，你有两个随机数生成器，每个生成一个数字序列。 你的计算机要处理的问题是：两个序列是完全相互独立的，还是以某种隐含的方式相关（一个序列是另一个序列的“傅立叶变换”）？ Aaronson在2009年引入了这个“傅相关”（forrelation）问题并证明它属于BQP。 这留下了更难的第二步 —— 证明“傅相关”问题不在PH中。



在某种意义上，这就是Raz和Tal做的事情。他们的论文实现了BQP和PH之间所谓的“oracle”分离。这是计算机科学中常见的一种结果，研究人员在他们真正想要证明的东西超出他们能力时所采用的结果。

区分BQP和PH等复杂度类的实际最佳方法是测量解决每个问题所需的计算时间。但计算机科学家“对实际计算时间没有足够的理解或测量能力，”多伦多大学计算机科学家Henry Yuen说。

因此，计算机科学家们希望通过测量一些其他的东西，来深入了解他们无法衡量的计算时间：他们计算出一台计算机需要询问“oracle”的次数以便对于问题有所回答。oracle就像一个提示者。你不知道它是如何提示的，但你确实知道它们是可靠的。

如果你的问题是弄清楚两个随机数生成器所生成的数字序列是否隐含相关，您可以询问oracle问题，例如“每个生成器的第六个数字是多少？”然后根据每种类型的计算机解决问题时需要提示的数量来比较计算能力。需要更多提示的计算机速度较慢。

“在某种意义上，我们更了解这个模型。 它更多地谈论信息而不是计算，“Tal说。



Raz和Tal的新论文证明，量子计算机需要比经典计算机更少的提示来解决相关问题。实际上，量子计算机只需要一个提示，而即使提供无限提示，PH中也没有可以解决问题的算法。 “这意味着有一种非常有效的量子算法可以解决这个问题，”Raz说。 “但是，如果你只考虑经典算法，即使你使用非常高级别的经典算法，他们也不能解决问题。”这表明，在有oracle的情况下，forrelation是BQP中的问题而且不是PH中的问题。

Raz和Tal在四年前几乎取得了这一成绩，但他们无法完成他们想要证明的其中一步。就在一个月前，Tal听到了关于伪随机数生成器的新论文的讨论，并意识到该论文中的技术正是他和Raz完成自己工作所需的技术。 “这是缺失的一块，”Tal说。

BQP与PH分离的消息很快传开。 “量子复杂度是复杂度领域中一块新的基石，”佐治亚理工学院计算机科学家Lance Fortnow写道，就在Raz和Tal发布证据之后的第二天。

这项工作提供了一个铁证，即量子计算机存在于与经典计算机不同的计算领域（至少在有oracle的情况下）。 即使在P等于NP的情况下 —— 旅行推销员问题就像在电子表格上找到最合适的线一样简单 —— Raz和Tal的证明表明仍然存在只有量子计算机才能解决的问题。

“即使P等于NP，即使做出那么强大的假设，”Fortnow说，“这还不足以攻克量子计算。”

更正2018年6月21日：本文的早期版本指出，旅行推销员问题的版本询问某条路径是否恰好是最短的距离“很可能”在PH中。 事实上，它已被证明属于PH。