论文题目：

Revealing in-block nestedness: Detection and benchmarking

论文地址：

https://journals.aps.org/pre/abstract/10.1103/PhysRevE.97.062302

 

1. 网络科学核心议题——

嵌套性和模块性

 

 1.1嵌套性和模块性

 

嵌套性（nestedness）和模块性（modularity）均是宏观结构的重要特征，一直是网络科学的核心议题。

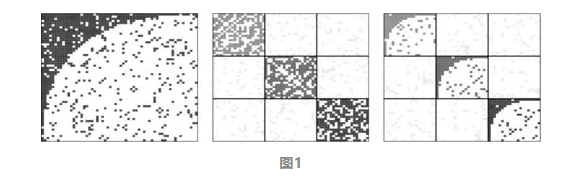
左：具有嵌套结构的网络。中：具有模块结构（block structure）的网络；模块在网络科学和生态学中分别被称为社群和群落。右：具有块内嵌套（IBN）结构的网络。模块内，网络节点呈嵌套结构。

嵌套性概念源于生物学。从结构上看，完全嵌套模式中，任一节点的关系的集合均包含于较高等级节点的关系的集合，见图1（左）。

模块结构，意味着节点存在次级群体，一节点内的连接紧密，节点间的连接较松散，见图1（中）。

嵌套性和模块性诞生于协作和竞争的动态冲突，因此，人们通常认为，它们是不兼容的。然而，越来越多的证据表明：在自然和社会生态系统中，两种模式共同存在。

 

 1.2 研究阻碍：方法论，认识论

 

复杂网络的结构是动态运行的结果。在了解动态运作方式前，首先要找到识别这些模式的正确方法。从仅有的文献中研究者发现了两种评估嵌套性和模块性的方法，但它们都忽略了这两种结构的相互作用，如块内嵌套（IBN）结构，见图1（右）。

除方法论挑战外，认识论方面，对系统边界的定义模糊问题依然不容忽视。因为研究人员不自觉地随意改变观察尺度。扩大观察尺度后，网络结构只会展现连接松散的模块。该问题在自然生态系统中尤为显著，同时存在于社交网络。

 

 1.3 研究成果及影响

 

本文解决了评估嵌套性和模块性结构的方法论问题。首先，提出了块内嵌套的概念，在某种程度上，一网络由内部嵌套的区块组成。然后，提出了在合成网络和大量真实网络中都能识别该结构的一套优化方法。

这些发现挑战了我们对生态系统和社会系统的拓扑结构的理解，呼唤能够解释这种模式涌现的新模型。

2. 无噪声合成网络的块内嵌套结构

 2.1 嵌套性度量

 

 2.2 模块性优化

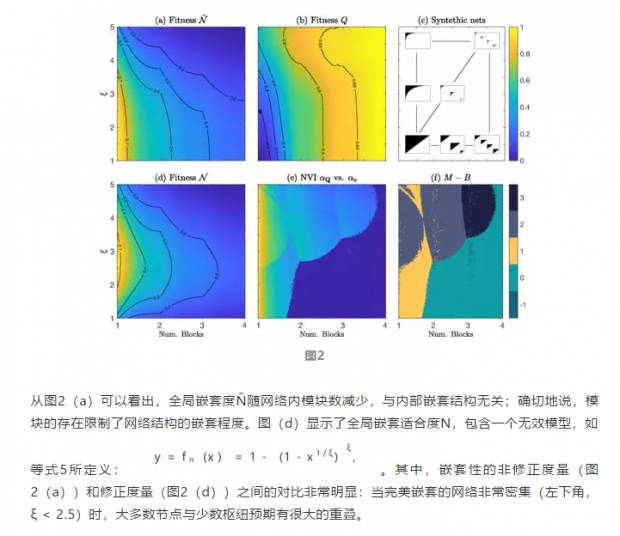
图2（b）说明了模块性Q随着网络中模块数增加，与嵌套结构的形状无关。图2（e）显示了模块性优化后的模块数与实际值（ground-truth，缩写GT）的正态变化。图2（f）显示了通过最大化Q检测到的模块数M与实际模块数B之间的差异。

图2（b）、图2（e）和图2（f）清楚地表明，将模块性和嵌套性作为两个独立的网络属性进行测量本质上是有缺陷的，模块性优化仅在大量模块和密集网络（右下角）的限制下才是可靠的。

 

3. 合成网络中块内嵌套结构的检测

 

作者通过分析大量来自不同学科的真实的网络，以证明该结构在不同性质的单一和双方网络中的普遍性。在本节中，我们首先介绍具有块内嵌套结构的基准图模型，然后介绍Q优化算法和I优化算法在重建这种结构时的性能结果。

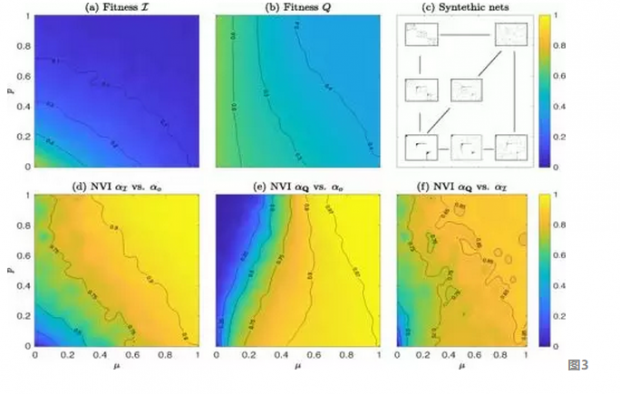
合成IBN网络的结果：对于变化的p值和μ值，有B = 3且ξ = 3 。图（a）通过仿生优化算法获得适应度函数I的值。同样，图（b）用组合优化算法计算得出模块性Q的值。图（d）和（e）通过信息的归一化变化（NVI）将优化后的I（ αi）和优化后的Q（ αQ）与实际值（α0）。图（c）将p和μ两参数对在综合生成网络的影响可视化。图（f）通过NVI比较了优化后的I （αI）和优化后的Q （ αQ）。

3.1 块内嵌套结构生成器

 

在完全嵌套的结构中，行（和列）与较大标度的行（和列）的子集相互影响，正确地排序其邻接矩阵，这些合成产生结构的一个例子如图 2（c）和图 3（c）所示。

 

 3.2块内嵌套优化应用于合成网络

 

图3显示了2600个网络上（p ，μ ）参数空间的详尽探索结果，其中固定的B = 3且形状参数ξ = 3（见图 3（c）所示的邻接矩阵）。模块性优化过程（图3（b））后，这些合成网络的结果显示：Q仅受p参数的轻微影响（即IBN的水平），即，不考虑模块内的任何特定结构，而只考虑内部密度。

图 3（a）显示了基于生物学启发的优化算法的最大化过程之后的块内嵌套适应度I的值，I对模块性和嵌套性都很敏感。着眼于Q检测分区相对于规定分区的相似性（图3（e）），I优化允许我们揭示沿μ轴的区域的实际分区，只要p保持低值（图3（d））。

参数区域对应于低p和高μ也是Q检测分区和I检测分区差异最大的区域（图3（f））。这指出当存在明确的内部嵌套结构并且存在大量的块间连接时，Q检测的分区特别不可靠。 

 

4. 决议限制

文章在第四节讨论了该结构的适用范围，并发现大量真实数据集中存在块内嵌套结构，且在生态和社会系统中普遍存在，只是受限于传统模块优化/嵌套探测方法的限制。

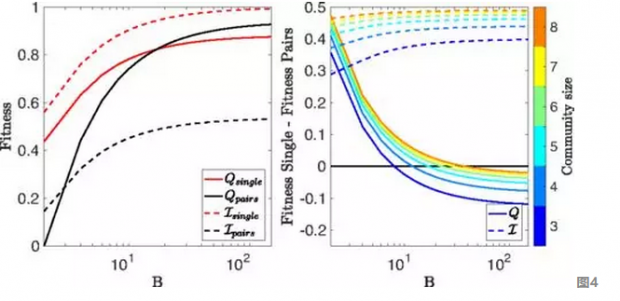
剩下： Q 单 （实心红线）和 Q 对。（实黑线）作为嵌套块数的函数， 乙（注意semilog标度）。与完全连接的派系一样， Q因为这个密集的子图环表现出一种矛盾的行为，显示出一种无视自然分区的交叉，有利于更大规模的分裂。 I单身（红色虚线）和 I配对（黑 - 黑线）用于相同的配置。

不像 Q， 一世揭示所有范围的自然分区 乙，即 I挑选 >I对，∀乙。此外，比例 I挑选 /I对 ≈0.5。对：两者之间的区别 I单身 和 I配对 （虚线），之间 Q 单 和 Q 对（实心），适用于不同的块尺寸（注意半尺度）。结果表明，左侧面板上提取的结论也适用于不同的设置。

如图4（左）所述，如果各社群没有改变，内部和外部连接之比保持不变，没有证据表明块内嵌套结构具有精度限制。此外，图4（右）确认了一些其他配置的这种行为。

5. 真实数据集中块内嵌套结构的检测

 5.1 块内嵌套结构

 

该系统具有清晰的块内嵌套结构，无法通过模块化的最大化来检测。图  5（c）显示了城市用户服务网络的结果。图5（d）显示了代表荷兰学校班级友谊关系的单一网络的结果。该网络的分析结论类似于图5（a）中的结论。

 

 5.2 局限性

 

虽然图5有助于直观了解I、Q和N的工作原理，但这些表示可能会产生误导。例如，图5（b）（右）中的度数排名表示  传达了这种特定的网络明显（和全局）嵌套的想法 - 但其他两种安排也具有定性上的说服力。出于这个原因，作者系统地比较了一方面的N和Q的结果，另一方面，I对上面提到的整套真实网络的结果。



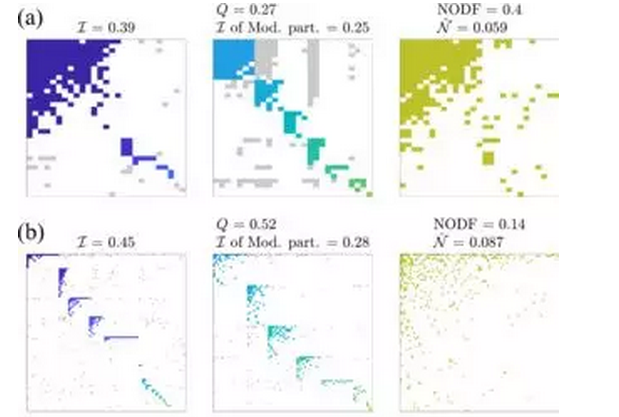
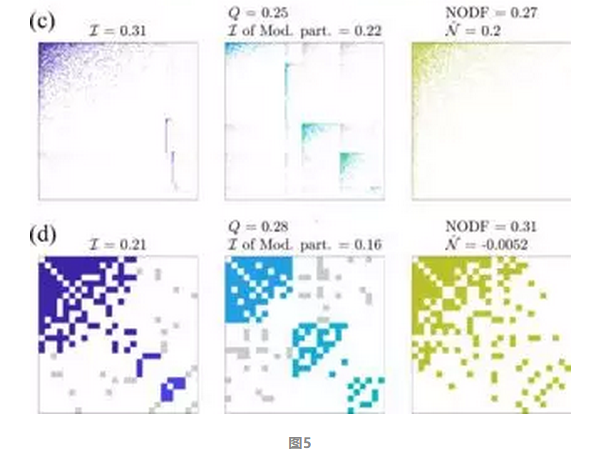
四个说明性系统的相互作用矩阵：（a）伏尔加 - 卡马自然保护区的宿主 - 寄生虫竞争性二分网络； （b）智利CordóndelCepo的一个授粉共生双方网络； （c）印度钦奈市民访问城市服务的城市双网网络； （d）荷兰学校班级的单一友谊网络。对于所有这些，已经安排了行和列来突出显示不同的方面：I - （左）和Q  -最大化（中心）分区的块成员资格和程度； 右栏中的全球学位排名。

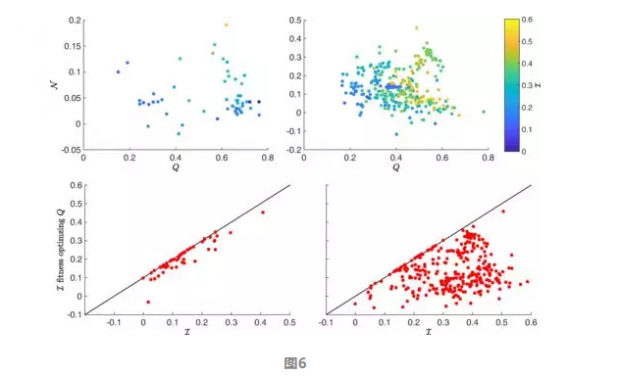
上图：使用I测量（颜色编码）将模块化和嵌套面临的散点图。每个点代表一个生态，城市或社交网络（左图：单一网络；右图：二分网络）。请注意，在Barber的模块化的基础上分析了二分网络。正如研究者提出，获得优化的模块化或直接在块嵌套性值的比较：底部I。 

此外，在图6（b）中，作者示出了通过最大化Q面对I自身的最大化而获得的分区的I值。这个图表证明模块化优化有时可能会使分区具有一些块内组织（靠近对角线），但大多数情况下它是盲目的。该结果强调，使用模块化最大化的方法，连续评估所识别的块内的嵌套性，无法在大多数现实世界的网络中揭示块状嵌套结构。