
世界是复杂的,我们总在试图去讨论复杂世界的背后有怎样的规则。在理论物理学家、圣塔菲研究所的前所长,杰弗里·韦斯特(Geoffrey West)眼中,有一种不变的标准可以衡量看似毫无关联的世间万物——无论是生物体的体重与寿命,还是互联网的增长与链接,甚至是企业的生长与衰败。这个法则是标准而统一、客观而美丽的,这就是规模法则。

杰弗里·韦斯特 | 现年78岁,世界顶级理论物理学家。全球复杂性科学研究中心、“没有围墙的”学术圣地——圣塔菲研究所前所长,入选《时代周刊》全球最具影响力100人。数十年致力于“规模”的研究工作,其研究成果被应用在理解生命体、城市可持续发展、企业运营等众多领域,被业内奉为“跨学科诺贝奖”的不二人选。
在本次活动中,我们邀请了北京师范大学教授张江、电子科技大学教授吕琳媛,为我们揭示《规模》所代表的新的世界观与新的规律。
两位老师的现场精彩讲座,现在可以回看录像啦!扫描上方二维码即可在微信观看。
或从电脑浏览器进入录播课教室观看:
吕琳媛:
复杂世界,简单规则

大自然是绚丽而精彩的,虽然人类的认知有限,但我们也发现了上百万种动物,40多万种植物6000多种语言……在大大小小的自然系统的背后是否存在着普适、简单的规律呢?
事实上,规律是存在的,杰弗里·韦斯特,作为复杂系统领域的专家,经过20余年的探索找到了这种规律——这就是规模法则。

什么是规模法则?
针对复杂系统地探讨总是让人兴奋,特别是针对物理学家而言——因为物理学总是在探寻在纷繁复杂的现象之后的最本质的规律。
规模法则所探讨的是在纷繁复杂的世界背后的量化法则,有了规模法则,我们可以更加科学理性的看待系统的演化与生长,也能去解释大量的现实世界的现象。比如——
“为什么我们不能长生不老?”
“为什么哥斯拉这样的怪兽在现实中不可能存在?”(后附)
“为什么树木不能永远地生长?”
“为什么不同哺乳动物一生的心跳次数大约都是15亿次?”
“为什么公司会衰亡而城市却一直存在?”
这些问题看起来似乎毫不相关,但其实他们都可以用规模法则解释。
规模法则,实际上就是Y~X^α,这个公式的含义是Y正比于X的α次幂,其中的X通常是代表系统规模的变量,他可以是人的体重、公司的员工数量、城市的人口等,而Y可以代表系统中的其他可量化的指标,真正决定系统性质的,是幂指数α。

如果α<1,说明系统是亚线性的增长模式,这意味着系统的规模翻了一倍,Y的指标可能只增长了69%。而当α>1时,系统是超线性的,Y指标则会比系统规模增长的更快,比如规模翻一倍,Y增长了120%。
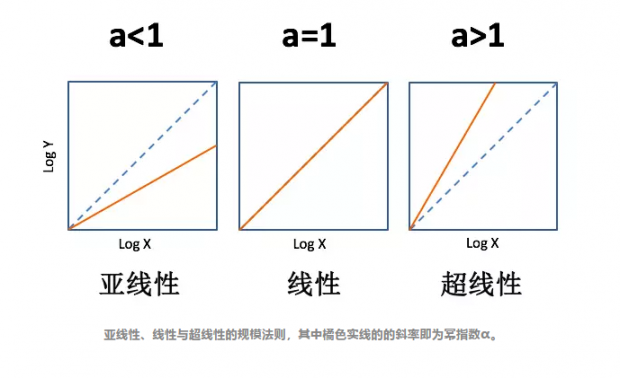
自然界中的规模法则
在自然界中存在着大量的例子可以被规模法则所解释。
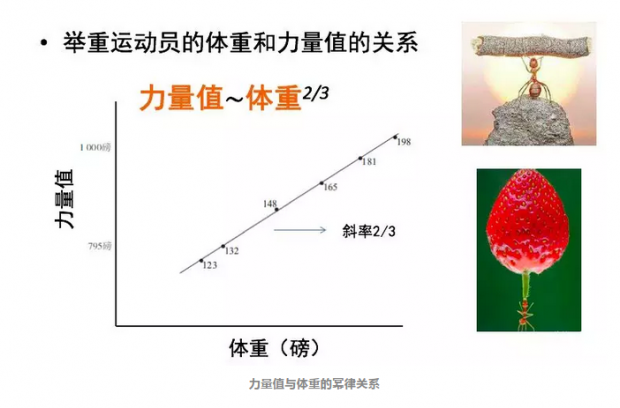
例如,不同物种的力量与体重呈现亚线性关系,这表明生物体的力量并不直接关联于体重,而是关联与体重的2/3次方,体重越大,力量随着体重的增长就越不明显,相反的,体重越小,生物体“看起来”就越有力量,这解释了为什么小蚂蚁可以举起比自身重量大好几倍的东西,而人类则不能。
又如,著名的克莱伯法则阐述了代谢率与体重的关系:在不同物种之间——小到老鼠大到大象,代谢率都与体重的3/4次幂成正相关(这同样是一个明显的亚线性关系),然而维持身体的需求又正比于体重。
这就表明,随着生物的成长,总有某个时刻,他们通过代谢摄取的能量已经不足以支撑体重的进一步增加,所以生物体的体重总是有限的,没有生物体的体重可以无限的生长下去。
怎样让公司
像城市一样长青?
除生物体外,公司与城市同样符合规模法则,但又与生物体不同,公司的规模法则是近乎线性的,而城市的产出与城市规模是超线性增长的:这说明城市的人口越多,城市的基础设施的利用率就越高,这意味着当城市人口增加了一倍,可能只需要增加85%的加油站。
由于这三种系统有不同的规模法则,因此我们可以看到他们的命运是完全不同的:生命体的寿命总是有限的,公司也难以逃脱衰老的命运,而城市则可以发展下去。

对公司而言,其模式是可以被人为改变的。也就是说,以前,人们总在考虑是否能让公司像生物体一样代谢,但像生物体一样代谢就意味着公司的寿命是有限的。
因此,现在,人们开始思考怎样让公司像城市一样实现超线性的增长,从而逃脱死亡的命运。这背后有怎样的差异?
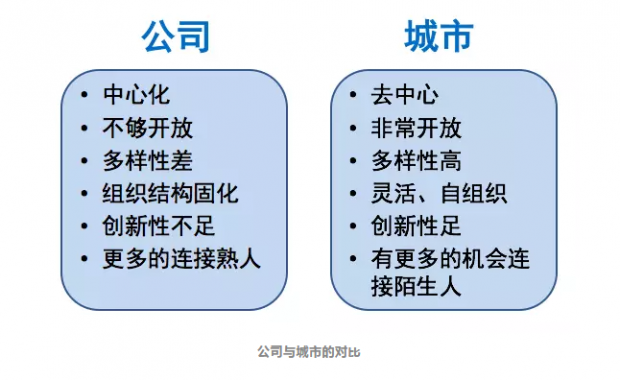
随着规模的增加,固化的组织结构带来的负面影响越来越大,那么应该怎么做呢?
其实一些大企业已经意识到这些问题,像阿里巴巴和腾讯这些大公司都在做着一些新的尝试。他们在公司内部引入竞争机制,鼓励员工内部创新,这种模式存在的意义在于打破公司僵化与固定的架构,从激发更多的创造力。另外,他们也加强了与外界的沟通,比如会去做一些开放的平台,这些就像基础设施,吸引更多外部的新鲜血液进入他们的企业生态中,提升多样性。
复杂性背后的简单机制
虽然我们看到的事物完全不同,但他们背后的机制可能是相同的,而且是简单的。复杂性可以从简单性中涌现出来,材料科学最新研究表明,把很多物质单元放在一起,只控制温度这一个变量就可以生长出各种各样的花朵,这给我们的启发是,复杂世界的背后一定存在更本质、更简单的制约因素,我们需要像物理学家一样思考,揭开面纱看到事物的本质。

无标度网络模型就是一个极其简洁的机制的阐述,它的基本假设是:系统会随时间增长,一个新节点与一个“老”节点相连接的概率正比于这个“老”节点的度(优先连接机制)。通过这样简单的机制就可以产生无标度网络。现实中,很多网络都具有无标度特征。
无标度网络告诉我们,网络中节点的角色大不相同,大多数节点的度都很小,只有少数节点的度很大,但这些大度节点却对网络的结构和功能起到重要作用。比如,把它们中的一些去掉,网络会很快破碎。
我们经常看到一些商家找网络上的红人,或微博大V用户转发他们的商品,这实际上是利用了这些名人在网络中的高传播影响力。正因为社交网络的无标度特征,才使得这种营销活动能够有效。
除此之外,还有大量的机制性的突破等待着科学家们的探寻。
因此,无论是城市规划,还是公司运营,人们都无法忽视规模法则的重要性,我们必须学会以规模的角度考虑事物量变时的非线性效应,正如杰弗里·韦斯特所说:
一座城市或一家公司的经济产出、繁荣、创意和文化都根植于其居民、基础设施和环境的多重反馈机制的非线性特质。
张江:规模的背后——
关于规模法则本质的探寻

什么是规模(Scale)?规模在英文中并不只是表达了一种大小尺度的关系,而更有一种拉伸、缩放的含义,在你使用缩放的视角,从多个尺度对系统进行观察的过程中,有很多非线性的有趣性质将会体现出来。
人类常有一种线性的直觉:我们会自然地认为哥斯拉就应该是一个身高数十米的人形怪兽,从直觉角度,我们也会感觉两个5寸的披萨要比一个9寸的披萨更大——但实际上披萨的面积与半径成平方关系——也就是说,披萨面积的一次方与直径的二次方成正比:这就是幂律。
复杂系统的
研究脉络是什么?
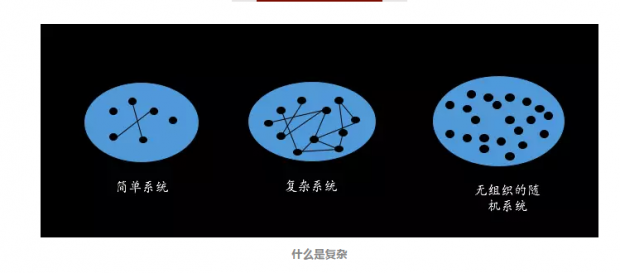
复杂系统的研究脉络实际上是与物理学的研究脉络类似的,虽然目前,科学家们还不能将支配复杂系统运作的法则还原为牛顿定律那样简洁的规律,但他们依然在沿用物理学研究的范式——就如同第谷、开普勒、牛顿的研究脉络一样:第谷收集了大量天体运行的数据,开普勒总结出了开普勒三定律——从椭圆曲线的假设出发,用方程描述了天体的运动定律,而牛顿的万有引力定律才真正描述了这一切现象背后的机理,击中了天体运动的本质,万有引力定律甚至可以推导出开普勒三定律。
复杂系统领域的研究也正在沿着这样的科学脉络进行着,在大数据时代,人们积累了大量的有关于自然系统和人工系统的数据,而科学家们也在不同领域发现了幂律法则——即用公式去描述Scaling的现象,从城市,到生命,再到公司。至今,科学家们已经提出了很多更本质的假设,并且有的已经得到了实证数据的支持——科学家们正在试图逼近大量现象背后的普适机理。
克莱伯法则——
生物界的开普勒定律
早在1932年提出的克莱伯法则(Kleiber's law)描述了新陈代谢与体重大小之间的关系:对于很多哺乳动物来说,其基础代谢率水平与体重的¾次幂成正比,这个定律的适用范围极其广泛,横跨了20个数量级。(后经杰弗里·韦斯特扩充的克莱伯法则可以横跨近30个数量级,甚至细胞中的线粒体都同样被克莱伯法则所约束)
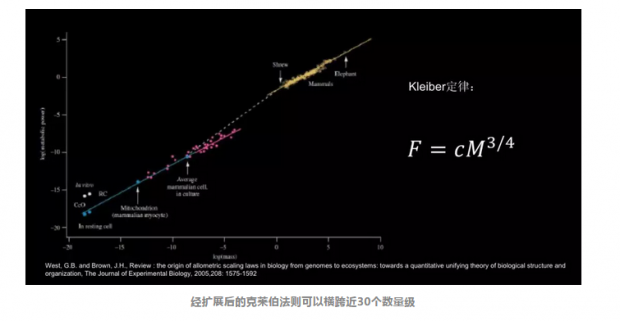
克莱伯法则就是一种典型的规模法则,它的内在机理是什么?
一个看似很有道理但错误的解释是:就如同披萨的半径平方与表面积成正比关系。生物体的代谢是与表面积正相关的(例如皮肤排汗行为),而生物体的重量则是和体积正相关的,因而我们似乎可以推导出代谢关联于以平方项表示的表面积,重量关联于以立方项表示的体积:代谢与重量成2/3次幂的关系。
但实际上是3/4次幂,到底是哪里出了差错?
如果假设生物体是生活在四维时空中(表面积将会是一个三次方项,体积将会是四次方项),一切就都会变得合理起来。
那么第四个维度从哪里出现?杰弗里·韦斯特提出了一种解释:新的维度来源于分形。
——分形为什么可以升维?
一个典型的例子是皮亚诺曲线:在正常的观念中,曲线是1维结构,而皮亚诺曲线通过分形——无限的,自相似的折叠和弯曲,填满了一个二维空间,使我们可以认为这个曲线是二维的。

生物体内部存在着大量的分形结构,例如人的血管,树木的枝杆,正是经过亿万年演化的分形结构给了我们每个人极其高效的代谢,使我们不能将生物体看作简单的三维世界中的物体,而更应该被看作四维空间中的生命。
这样,2/3次幂的关系就能够被很自然的转变为3/4次幂的关系,杰弗里·韦斯特从本质的角度给出了对克莱伯法则的解释。
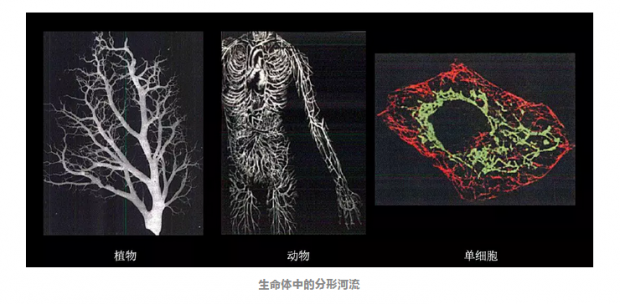
生物体中的规模法则可以给我们的生活以直观的启示:我们不能以线性的角度来看待生物的代谢行为。例如:当小朋友的体重很轻时,他的代谢比你想象中更快,这意味着他能更快的消化食物,也能更好的消化吸收药物——由于3/4次幂法则的存在,我们需要更谨慎的对待小朋友的药物使用问题。
科学家们曾经做过这样的实验:给大象注射一种致幻药物,他们观察到大象的体重约是猫的3000倍,所以直接将猫的安全剂量乘以3000注射给大象。令所有人都没想到的是,注射5分钟后,大象轰然倒下,进入持续的癫痫状态,一小时四十分后,大象直接死亡。
正是由于对规模法则的不了解,使人们“直觉地”认为大象的抗药性与代谢速度、重量成正比,害死了这头大象。若人们以3/4次幂的规律去重新计算药量,大象可能会安全得多。
城市中的规模法则

从飞机上观察,城市就像一个有机体,它的道路就像人的血管,车流就像在输送养料。
同样,在城市中也存在着大量的规模法则:专利数量、经济总量、研发投入、加油站的数量、道路总长度等等等等。其中有一些变量与人们之间的互动尤其相关——例如GDP、专利总数、犯罪数、总工资等,这些变量与城市规模的关系尤其吸引人的兴趣,实际上,城市的人口总数与其他变量之间存在着1.15次幂的关系。
这意味着:随着城市规模的扩大,不但城市的总财富会增长,人均的财富也会增长,这就是大城市会在不断吸引年轻人留下来奋斗的原因。
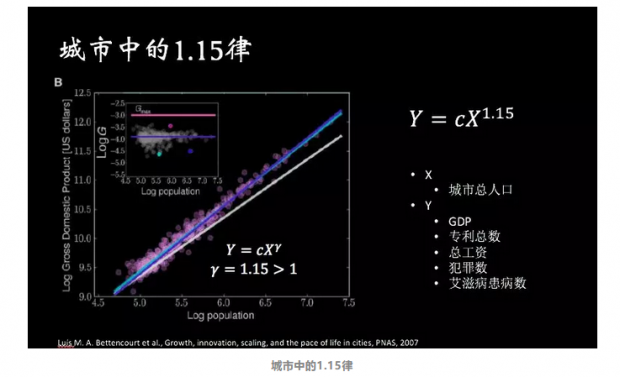
不仅是针对实际的城市,对虚拟的在线社区而言,规模法则同样存在,社区用户的活跃人数与社区内的成员交互(如发帖、发文章数量)之间依然存在着超线性的规模法则。
我们可以这样理解城市的超线性规模法则背后的机理:假设社区内的任意两个人都能够无任何障碍发生交互的话,那么社区内产生的总交互数量将是人数的平方,而前文中提到的变量都是和交互密切相关的变量——这些变量就会与人数的平方成正比。
但在现实世界中,人们受限于圈子、认知或物理上的限制,使人们无法无障碍地和任何人交互,这就使得幂次从2下降至城市中的1.15。
进一步的,张江等人提出了匹配生长模型来描述社区的生长:在社区很小的时候,社区的特点是鲜明的,这就意味着社区资源与多样性都不够丰富,新的成员想要加入社区可能存在着困难。
但随着社区的成长,社区的多样性在不断增强,社区变得越来越丰富和包容,新的成员加入的限制就会大大减小,因为新成员能够很容易的找到社区中与他类似的人并建立联系,所以社区生长得越来越迅速。
有趣的是,这个模型不但能够描述社区的状态,同样可以很好的描述美国境内沃尔玛超市的生长和扩张。同时,这个模型还可以很好的对城市的生长进行建模。

还有一些研究展示了城市新陈代谢与城市规模的关系。什么是城市的新陈代谢?
杰弗里·韦斯特假设城市的新陈代谢与城市的GDP成正比(在一些研究中,我们可以看到国家的碳排放量与GDP的确成正比关系),那么城市的代谢将与城市的规模成幂律关系,规模越大,城市的代谢越快。
一个很有趣的研究关注了城市的规模与城市中人均步伐速度的关系,结果发现仍然符合规模法则的,大城市的人们步伐紧张,小城市的人脚步舒缓,这表示随着城市规模的扩大,人们变得越来越紧张和忙碌。
城市的代谢在加速,而作为城市组成单元的我们就会越来越忙碌,融入大城市的生活的会让你越来越紧张,你会收到处理不完的邮件,会有大量的人和你形成强链接,你们会给彼此施加很大的压力。
更进一步,城市的代谢可以和城市的生长方程相结合,因为超线性增长的关系。
科学家们发现,城市的代谢是在加速的,而城市的维护成本则并不与城市的规模成超线性关系(通常情况下,维护成本与城市规模成线性关系),一旦城市的流入能量超过了维护成本,城市将会以更快的速度不停生长,这是杰弗里·韦斯特最为有趣的推论之一。
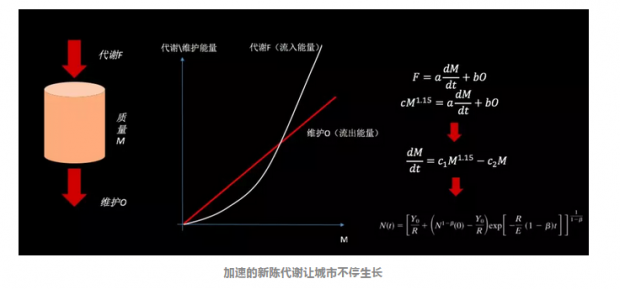
根据这样的生长方程,城市会很快在有限时间内达到无穷大的规模——这样的城市在现实中并不存在——这说明存在着某些原因阻止了城市在有限的时间内的爆炸性增长。
杰弗里·韦斯特给出了这样的解释:城市的生长过程,是一个新陈代谢的过程,需要消耗物质能量,一旦能量供应不足,方程的条件就会被破坏,如果不人为干预,城市很可能会走向崩溃。
但城市没有崩溃,是因为城市中存在着科技创新,每一次科技创新都在创造着新的生产力,重塑着城市的运转规则——使城市趋向更高效的运转(移动互联网、电子商务、人工智能无一不是如此),这种科技创新也会重塑城市的生长方程,使得城市的生长过程被重启。
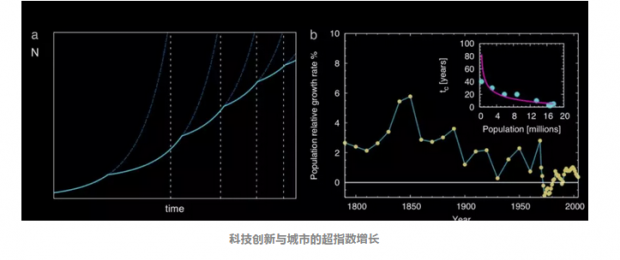
但也存在着另一个无法忽视的现象:科技创新周期正在被不断地缩短——互联网的普及用了大约二十年的时间,而移动互联网的普及只用了五年,今天的人工智能正在以难以想象的速度浸入人类社会的每一个角落。
因此,如果按照这样的城市生长方程去推演,总有一天科技创新的周期会接近无限短。这说明,从乐观的角度来看,城市的GDP、总工资都会迎来暴涨,而与之相对的,城市内的犯罪率,环境破坏与艾滋病的传播也会迎来高峰——
在不久的将来,天堂将与地狱同在。
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 