阅读：0
听报道
导语
康奈尔大学计算机科学系教授Chris De Sa 与斯坦福大学计算机科学系博士生Albert Gu 携手构建出高效的嵌入算法——使用双曲线组合结构嵌入算法，以更低的维度更好地嵌入文本、知识图谱等非结构化的数据。
编译：集智俱乐部翻译组
原题：HyperE: Hyperbolic Embeddings for Entities
神奇的双曲线嵌入算法
最早在2017年，Nickel＆Kiela提出了使用双曲线代替欧几里得嵌入空间来表示分层数据(该过程也称嵌入)，并且在嵌入图形时表现出了较好的结果。
由此，双曲线嵌入在机器学习界引起了广泛的关注。那么双曲线嵌入相对于传统的嵌入方法有什么优点？
双曲线嵌入可以在很少的维度上保留图形实体间的距离
充分表达层级结构
今天介绍的的这篇文章提出的一种双曲线嵌入的算法，该算法不仅可以完成知识库处理相关的任务，并且可以作为一个用来处理NLP任务，例如Question & Answering等。
在论文中，作者提出了解决优化潜在问题的新方法，并阐明了如何权衡每种方法。当嵌入分层数据结构（如同义词或类型层次结构）时，双曲线嵌入可以用较少的维度，表达出复杂的网络信息。
例如，给定一棵树形的网络，该论文给出了一个组合结构，可以将树嵌入双曲空间中，在不使用优化算法时就可以达到较低的失真率。在WordNet上，在双曲空间中只使用了两个维度，该嵌入算法平均精度（MAP）就达到了0.989，Nickel等人提出的双曲空间结构使用200维也只获得了0.87的平均精度。
为了嵌入一般度量空间，论文中提出了多维尺度（h-MDS）的双曲线推广算法。该算法展示了如何从距离中精确恢复双曲点，算法显示，即使在维度很少的情况下，h-MDS算法也可以很好地恢复双曲点。
数据库及源码下载
论文在如下三个层次网络中做了双曲嵌入的实验，这些网络分别为：WordNet、Wikidata、UMLS（统一医学语言系统）和MusicBrainz（开放数据音乐数据库）。该算法通过“相似性”和“类比”的双曲线评估嵌入的好坏。并基于PyTorch实现了一个可以处理不完整信息并且可扩展的HyperE 嵌入算法。文章中各种实体嵌入可以在下面以GloVe格式下载。
WordNet：https://wordnet.princeton.edu/
Wikidata：https://www.wikidata.org/wiki/Wikidata:Main_Page
UMLS：https://www.wikidata.org/wiki/Wikidata:Main_Page
MusicBrainz：https://musicbrainz.org
读者们可以在GloVe格式的WordNet，Wikidata，UMLS和MusicBrainz中以各种维度（10d，20d，50d，100d）下载64位精度的实体嵌入。因为双曲线嵌入与欧几里得嵌入不同，嵌入的比例因子不是固定不变的，因此作者在顶行中写明了嵌入的比例因子。
通过将知识图谱中实体对应的双曲线距离除以所提供的比例因子，可以近似地恢复实体之间的输入图形的距离。该算法还提供了预处理脚本以创建输入图的边缘列表。这里还可以使用作者的公开的代码来查看如何使用双曲线实体嵌入。
实现双曲实体嵌入的公开代码：
https://github.com/belizgunel/hyperE/tree/master/demo
来自Wordnet的WordNet Hypernym，域主题和成员全名层次结构。（WordNet.zip 161MB）
https://stanford.box.com/shared/static/u06nzqy2eyi6eh01830ci156giepxrj0.zip
Wikidata实体层次结构，包括来自各个领域的100个属性，包括生物学，体育，经济学，政治学，计算机科学等等。（ Wikidata.zip 2.15GB）
https://stanford.box.com/shared/static/ozkvxryzib6kmjad9hyb0emq84to2ssz.zip
UMLS诊断层次结构来自ICD-9-CM和UMLS的ICD-10-CM词汇表。（UMLS.zip 123MB）
https://stanford.box.com/shared/static/yk0nwnix1a9nda13ws5hbdetm4zo9mvw.zip
MusicBrainz来自MusicBrainz的样本艺术家，专辑和歌曲层次结构。（MusicBrainz.zip 16MB）
https://stanford.box.com/shared/static/8anfeaia53pwsagvag9g6rlys932sj00.zip
双曲空间中的“词类比”
在许多自然语言处理（NLP）应用中，将词嵌入欧几里得空间中可以成功地编码单词之间的语义关系。评估词嵌入效果好坏的一种方法是“词类比”准确度。比如，经常在小学语文卷子中出的填空题目：
“北京(a)对中国(b)=华盛顿(c)对______ ”。
传统的NLP模型GloVe模型通过嵌入的余弦相似性找到词d，d的词嵌入最接近向量b -a + c。
在HyperE嵌入算法中，作者使用双曲线距离长短作为相似度量，距离越小相似性越高。换句话说，将具有最小双曲线距离的向量d作为b -a + c双曲线模拟的输出。我们将这个类比实验扩展到Wikidata中的实体层次结构，并尝试了一些具有不同关系的样本。
下边的表格是使用文章中的组合方法生成的实体嵌入做“词类似问答“的结果。嵌入为10维，64位精度。可以看出嵌入向量d正确的回答了”词类似“问题。
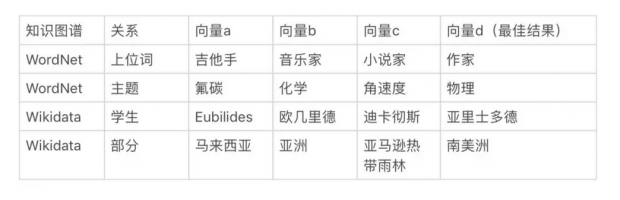
检测关系
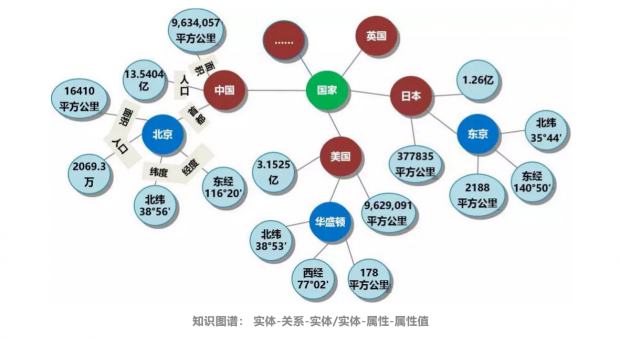
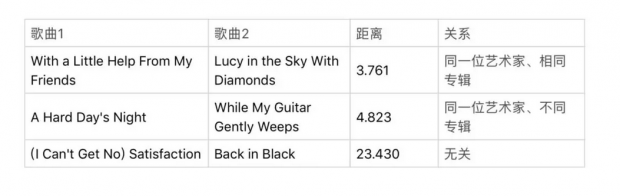
在音乐数据嵌入中，歌曲 - 专辑连边权重为2，专辑 - 艺术家连边权重为1.我们可以使用这些权重和嵌入式层次结构通过简单地计算嵌入点之间的双曲线距离来检测实体之间的关系类型。
例如，第一行的两首歌曲来自甲壳虫乐队的“Sgt.Pepper's Lonely Hearts Club Band”专辑，文章的嵌入识别出了这种关系。接下来第二行的两首歌是披头士乐队的歌曲，但来自不同的专辑。最后，滚石乐队和AC / DC乐队的歌曲显示为无关，双曲线中距离的远近可以很好的表示两首歌曲实际关系的远近。
嵌入效果
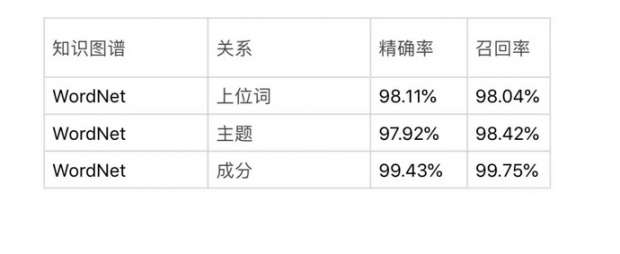
与欧几里得空间相比，双曲空间能够将知识图谱中的层次关系信息压缩到非常少的维度。保留几个输入的关系图中实体对之间的关系，通过实验的准确率及召回率的结果我们得知：双曲线空间嵌入通过保持实体间的距离实现多层嵌入。在此任务中，“正确”代表着，如果输入图形中的实体对有一条连边，则最终实体嵌入之间的双曲线距离除以基于输入图形计算的比例因子之后应当保持在1（±0.01）内。
每一个嵌入都是使用我们的组合方法生成的，维度是10维，精度为64位。下图是HyperE的精确率和召回率。
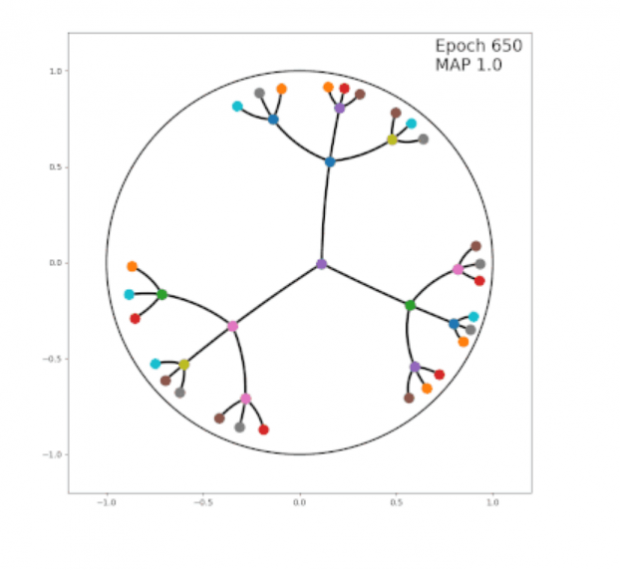
双曲空间可视化
在欧几里得空间中，圆周和圆盘区域分别随半径线性、平方地增长。然而，在双曲空间中，它们都相对于半径呈指数增长，这一性质特别有利于嵌入树型的分层结构。
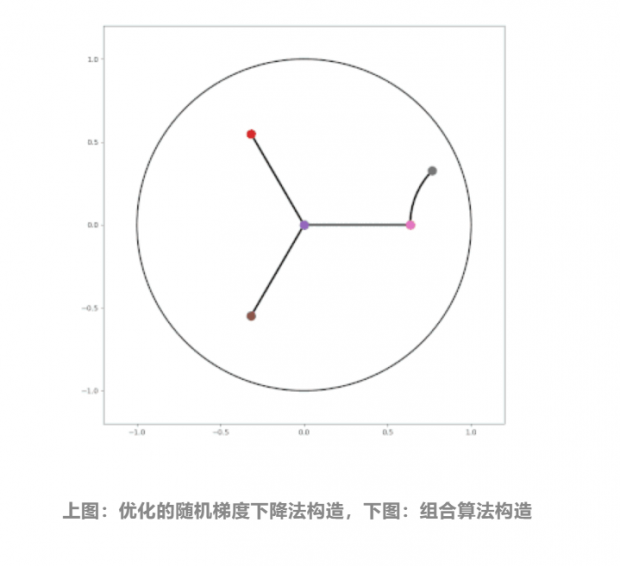
下面介绍了不同嵌入方法的一些可视化。左图是使用作者基于随机梯度下降的优化方法嵌入一个简单的树，它最小化基于双曲线距离的损失函数。对于相同的输入图，右图是使用作者提出的组合结构，这是一种确切的算法，可以精确地放置树顶点。关于组合算法，在作者的论文中有详细的阐述。
论文题目：Representation Tradeoffs for Hyperbolic Embeddings
论文地址：https://arxiv.org/pdf/1804.03329.pdf
相关工作
双曲线嵌入的研究是由最近的研究论文推动的，这些论文表明双曲线表示适用于各种层次结构，应用包括Tay等人的问答（QA）系统——HyperQA （2017），Chamberlain等人的顶点分类器（2017），以及Nickel＆Kiela（2017）中的链路预测。
Ganea等人（2018）提出了嵌入蕴涵关系，即用带有双曲锥的有向无环图作为启发式算法。Dhingra等人（2018）研究了双曲词和句子嵌入。其中许多论文使用双曲线几何的庞加莱模型 ; 作者的的工作和Nickel＆Kiela（2018）认为其他模型，如双曲面空间的双曲面模型，对于某些任务可能更简单。当然，总是可以在模型之间进行转换。
最近的研究方法试图将双曲线运算添加到神经网络中。Gulcehre等（2018）使用双曲面模型引入了双曲线形式的注意力机制。
双曲线运算也可以应用于支持向量机，如Cho等人的研究（2018）。
基于双曲线优化的下降方法也有了新的应用研究; 这些研究作品包括Enokida等（2018）用于测地线更新，Zhang和Sra（2018）用于加速黎曼梯度法，而Wilson＆Leimeister（2018）用于使用双曲面模型在双曲空间中进行梯度下降。
参考文献及论文地址
1.HyperE (2018) Representation Tradeoffs for Hyperbolic Embeddings
https://arxiv.org/pdf/1804.03329.pdf
2.HyperQA （2017）Hyperbolic Representation Learning for Fast and Efficient Neural Question Answering
https://arxiv.org/pdf/1707.07847.pdf
3.Chamberlain（2017）Neural Embeddings of Graphs in Hyperbolic Space
https://arxiv.org/pdf/1705.10359.pdf
4.Nickel＆Kiela（2017）Hyperbolic Representation Learning for Fast and Efficient Neural Question Answering
https://arxiv.org/pdf/1707.07847.pdf
5.Ganea (2017) Poincaré Embeddings for Learning Hierarchical Representations
https://arxiv.org/pdf/1705.08039.pdf
6.Nickel＆Kiela（2018）Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry
https://arxiv.org/pdf/1806.03417.pdf
7.Gulcehre（2018) Hyperbolic Attention Networks
https://arxiv.org/pdf/1805.09786.pdf
8.Hyunghoon Cho (2018) Large-Margin Classification in Hyperbolic Space Hyunghoon Cho
https://arxiv.org/pdf/1806.00437.pdf
9.Enokida (2018) Stable Geodesic Update on Hyperbolic Space and its Application to Poincaré Embeddings
https://arxiv.org/pdf/1805.10487.pdf
10.Zhang&Sra（2018）Towards Riemannian Accelerated Gradient Methods
https://arxiv.org/pdf/1806.02812.pdf
11.Wilson＆Leimeister（2018）Gradient descent in hyperbolic space
https://arxiv.org/pdf/1805.08207.pdf
12.Octavian-Eugen(2018) Hyperbolic Entailment Cones for Learning Hierarchical Embeddings
https://arxiv.org/pdf/1804.01882.pdf
13.Bhuwan Dhingra （2018）Embedding Text in Hyperbolic Spaces
https://arxiv.org/pdf/1806.04313.pdf
作者：Beliz Gunel, Fred Sala, Albert Gu, Christopher Ré
译者：陈孟园
审校：谷伟伟
编辑：集智小编
原文：https://hazyresearch.github.io/hyperE/
话题：
0
推荐
财新博客版权声明：财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有，未经博主及/或相关权利人单独授权，任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点，不代表财新网的立场和观点。
京公网安备 11010502034662号 