阅读:0
听报道

世界的法则被一些数字支配。
让我来用几个例子说明这句话的含义,π决定了所有圆周长和直径的比值,引力常数G决定了两个物体间万有引力的大小等等。这些奇妙的数字不仅在数学和物理中存在,而也在众多领域起到决定性作用,又比如生物学中的克莱伯法则告诉我们,大多数哺乳动物的基础代谢率与体重的3/4次幂成正比。

现在,让我来为你介绍近年城市科学界发现的另一个奇妙的数字:1.15,这个数字刻画了城市的规模。具体来说,城市的诸多指标与城市人口数的1.15次方成正比。这些指标包括城市的GDP、专利总数、总工资数、犯罪数甚至艾滋病病患人数。
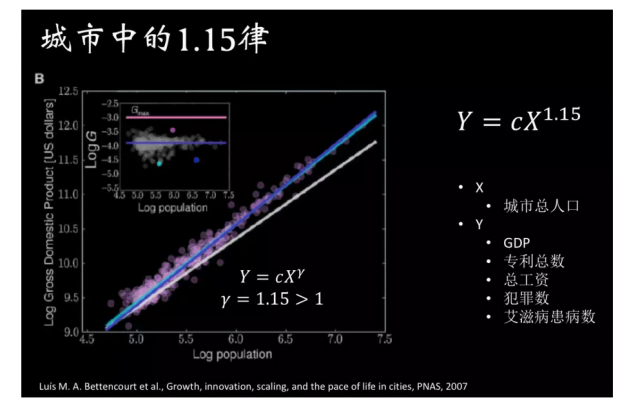
城市中的1.15律
这个奇妙的法则被称为城市中的1.15律。1.15律告诉我们,随着城市的增长,城市会呈现“超线性的繁荣和罪恶”——具体而言,这意味着城市的繁荣程度增长速度会快于城市人口数量的增长速度:每当城市人口数扩大两倍,城市的GDP、总工资等都将扩大两倍以上。同时,一些负面效应的影响也越来越显著:城市的犯罪数和艾滋病患病人数同样将会扩大两倍以上。
当然,并非所有的指标都严格遵循1.15次方的规律,但总体而言,决大多数指标都与城市人口数量的幂次呈正比关系,有些幂指数大于1,例如城市GDP与人口数的1.15次幂成正比,这意味着GDP的增长会比人口增长的更快,我们称这种幂指数大于1的现象为超线性增长。
而有的指标,例如城市的道路总长度则与城市人口数的0.83次幂成正比,我们称这种关系为亚线性增长关系。而所有幂律关系——不论是超线性的还是亚线性的,都被我们称之为城市中的规模法则,更详细来说,我们可以将已经发现的城市中的规模法则罗列如下:
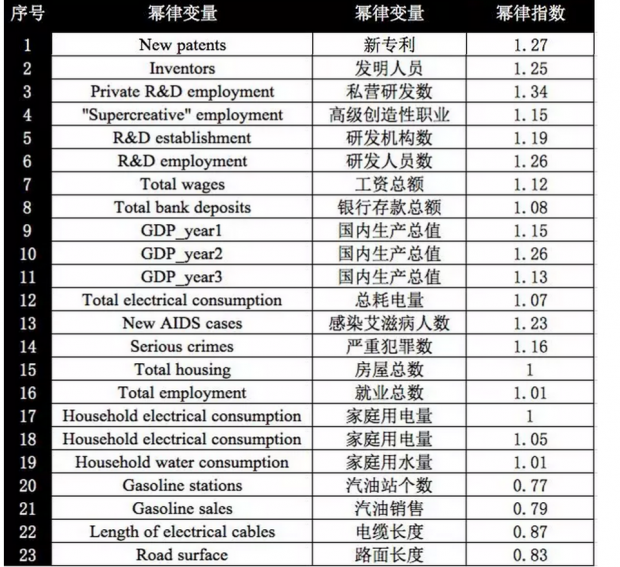
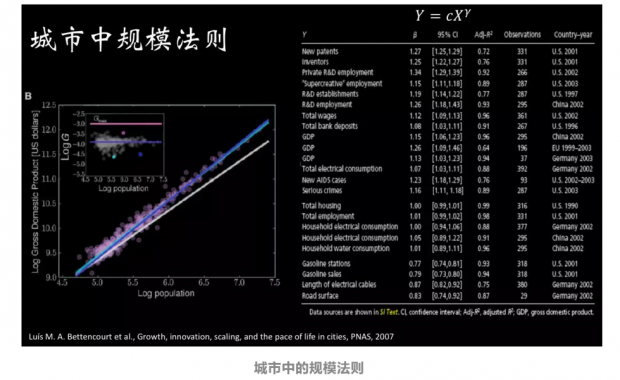
以1.15律为代表的城市规模法则的存在违反了我们的线性直觉——城市的量化指标并不与城市人口数呈正相关。为什么会出现这种情况呢?
实际上,以超线性法则为例:随着城市人口数量的增多,每一个人都更有机会与他人交互。交互的存在加速了人们的生产速度:每一个城市公民都有机会找到志同道合的朋友、同事。每一家公司都更有机会找到合适的合作伙伴。同时,随着交互成本的降低,犯罪和艾滋病传播的成本随之降低,这就导致了大城市更容易滋生犯罪。
除了城市规模法则之外,在这个世界中,还存在着大量超线性或亚线性的规则,这些规则的存在时刻挑战着我们习以为常的线性思维和世界观。如果你对此感兴趣的话,那么那么恭喜你找到了我们。
《规模》这本书既能让你见识一点儿世界的底层逻辑,了解一点儿物理学的“套路”,又能治愈某些流行的妄想。这本书最根本的思想,就是世间万事万物通常都不能按照简单的线性比例缩放,需要我们从线性思维过渡到复杂性思维。
编辑:孟婕
作者:张章
话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 