Nature长文综述：类脑智能与脉冲神经网络前沿-集智俱乐部的财新博客-财新网

在人工智能如火如荼的今天，基于人脑的“脉冲”（spiking）模拟计算框架下的脉冲神经网络（SNN）、神经形态计算（neuromorphic computing）有望在实现人工智能的同时，降低计算平台的能耗。这一跨学科领域以硅电路实现生物中的神经环路（circuit）为起点，现已发展到包括基于脉冲的编码以及事件驱动表示的算法的硬件实现。

2019 年 11 月 28 日，普渡大学的 Kaushik Roy、 Akhilesh Jaiswal 和 Priyadarshini Panda 在 Nature 发表长文综述，概述了神经形态计算在算法和硬件方面的发展，介绍了学习和硬件框架的原理。以及神经形态计算的主要挑战以及发展前景，算法和硬件的协同设计等方面的内容。本文是全文翻译。

编译：集智俱乐部翻译组

来源：Nature

原题：Towards spike-based machine intelligence with neuromorphic computing

前言

纵观历史，创造具有类人脑能力的技术一直都是创新的源泉。从前，科学家们一直以为人脑中的信息是通过不同的通道(channels)和频率传递的，就像无线电一样。如今，科学家们认为人脑就像一台计算机。随着神经网络的发展，今天的计算机已在多个认知任务中展现出了非凡的能力，例如，AlphaGo在围棋战略游戏Go中击败了人类选手。虽然这种表现的确令人印象深刻，但一个关键问题仍然存在：这些活动涉及的计算成本有多大？

人脑能够执行惊人的任务（例如，同时识别多个目标、推理、控制和移动），而能量消耗只有接近2瓦左右。相比之下，标准计算机仅识别1000种不同的物体就需要消耗250瓦的能量。尽管人脑尚未被探索穷尽，但从神经科学来看，人脑非凡的能力可归结于以下三个基本观察：广泛的连通性、结构和功能化的组织层次、以及时间依赖（time dependent）的神经元突触连接（图1a）。

神经元（Neurons）是人脑的计算原始元素，它通过离散动作电位（discrete action potentials）或“脉冲”交换和传递信息。突触（synapses）是记忆和学习的基本存储元素。人脑拥有数十亿个神经元网络，通过数万亿个突触相互连接。基于脉冲的时间处理机制使得稀疏而有效的信息在人脑中传递。研究还表明，灵长类动物的视觉系统由分层级的关联区域组成，这些关联区域逐渐将视觉对象的映像转化为一种具有鲁棒性的格式，从而促进了感知能力。

目前，最先进的人工智能总体上使用的是这种受到人脑层次结构和神经突触框架启发的神经网络。实际上，现代深度学习网络（DLNs）本质上是层级结构的人造物，就像人脑一样用多个层级去表征潜在特征，由来自输入过程中多个图层的不同潜在特征的表征，经过转换形成的（图1b）。硅晶体管硬件计算系统是这种神经网络的硬件基本。大规模计算平台的数字逻辑包含由集成在单个硅芯片上的数十亿个晶体管。这让人联想到了人脑的层级结构：各种硅基计算单元以层级方式排列，以实现高效的数据交换（图1c）。

尽管两者在表面上有相似之处，但人脑的计算原理和硅基计算机之间存在着鲜明区别。其中包括：（1）计算机中计算（处理单元）和存储（存储单元）是分离的，不同于人脑中计算（神经元）和存储（突触）是一体的；（2）受限于二维连接的计算机硬件，人脑中大量存在的三维连通性目前无法在硅基技术上进行模拟；（3）晶体管主要为了构建确定性布尔（数字）电路开关，和人脑基于脉冲的事件驱动型随机计算不同。尽管如此，在当前的深度学习革命中，硅基计算平台（例如图像处理单元（GPU）云服务器）已成为一个重要的贡献因素。

但是，使得“通用智能”（包括基于云服务器到边缘设备）无法实现的主要瓶颈是巨大的能耗和吞吐量需求。例如，在一个由典型的2.1Wh电池供能的嵌入式智能玻璃处理器（smart-glass processor）上运行深度网络，就会让处理器在25分钟内将电池消耗殆尽。

在人脑的指引下，通过脉冲驱动通信从而实现了神经元-突触计算的硬件系统将可以实现节能型机器智能。神经形态计算始于20世纪80年代晶体管仿照神经元和突触的功能运作（图2），之后其迅速演化到包括事件驱动的计算本质（离散的“脉冲”人造物）。最终，在21世纪初期，这种研究努力促进了大规模神经形态芯片的出现。

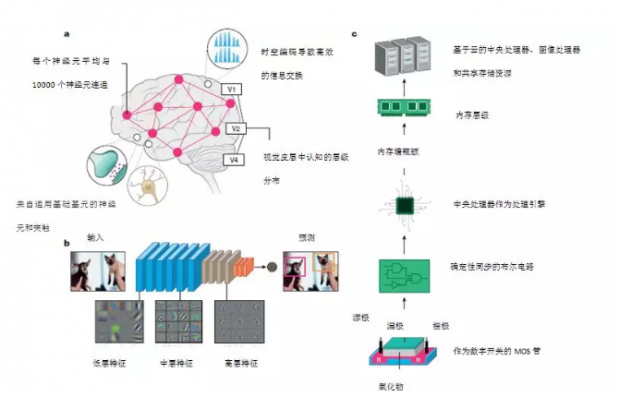
图1：生物和硅基计算的关键属性构架。a，大脑的组织原理示意图。神经元和突触与时间脉冲处理交织在一起的网络使得不同区域之间的信息能够快速高效地流动。b，一个深度卷积神经网络物体执行目标检测的图片。这些网络是多层的，并使用突触存储和神经元非线性学习广泛的数据表示。使用反向传播训练后，每层学习的特征都显示有趣的模式。第一层学习一般特征，如边缘和颜色斑点。随着我们深入网络，学习到的功能变得更具体，用对象的部分（如狗的眼睛或鼻子）代表完整的物体（如狗的脸）。这种从一般到特殊的过渡代表了视觉皮层的层次结构。c，最先进的硅计算生态系统。广义上讲，计算层次分为处理单元和内存存储。处理单元和内存层次结构的物理分离导致众所周知“内存墙瓶颈（memory well bottleneck）” 。当今的深度神经网络在强大的云服务器上训练，尽管会产生巨大的能耗，但仍可提供令人惊叹的精度。

今天，算法设计师们正在积极探索（特别是“学习”）脉冲驱动型计算的优缺点，去推动有可扩展性、高能效的“脉冲神经网络”（spiking neural networks ，SNN）。在这种情况下，我们可以将神经形态计算领域描述为一种协同工作，它在硬件和算法域两者中权重相同，以实现脉冲型人工智能。我们首先强调了“智能”（算法）方面，包括不同的学习机制（无监督以及基于脉冲的监督，或梯度下降方案），同时突出显示了要利用基于时空事件的表征。本文讨论的重点是视觉相关的应用任务，例如图像识别和检测。然后我们将探索“计算”（硬件）方面，包括模拟计算、数字神经运动系统，它们都超越了冯·诺依曼（数字计算系统的最新架构）和芯片技术（代表了基本的场效应晶体管设备，它们是当下计算平台的基础）。最后，我们将讨论算法的硬件协同设计前景，说明算法具有用于对抗硬件漏洞的鲁棒性，可以实现能耗和精度之间的最佳平衡。

一、算法展望：脉冲神经网络

脉冲神经网络

按照神经元功能，Maass开创性的论文将神经网络分为三个代际。首先，第一代被称为McCulloch–Pitt感知机，它执行阈值运算并输出数字（1、0）。基于sigmoid单元或修正线性单元（ReLU），第二代神经元单元增加了连续非线性，使其能够计算一组连续的输出值。第一代和第二代网络之间的非线性升级在扩展神经网络向复杂应用和更深度的实现方面起着关键作用。当前的DLNs在输入和输出之间具有多个隐藏层，都是基于第二代神经元。实际上，由于它们连续的神经元功能，这些模型可以支持基于梯度下降的反向传播学习，这也是目前训练深度神经网络的标准算法。

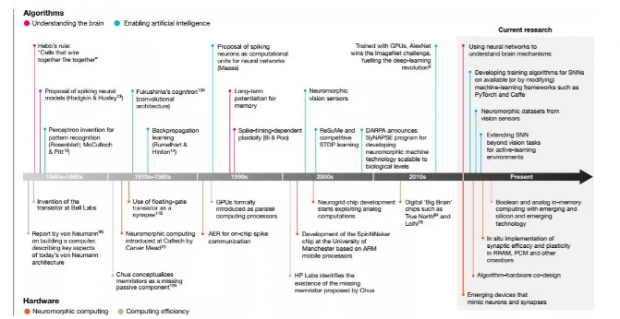
图2：智能计算的重大发现和进展时间表（从1940年代到当代）。硬件方面，我们有从两个角度展示发现：一是对神经形态计算的启迪，或通过硬件创新实现类人脑的计算和“智能”；另一方面是对计算效率的启发，或者实现更快、更节能的布尔计算。从算法的角度来看，我们已指出这些发现是出于理解人脑的动机，受到神经科学和生物科学的驱动，并同时致力于实现人工智能，它由工程和应用科学所驱动。请注意，这张图并不是完整或全面的清单。“当前研究”并不一定意味着过去没有对这些努力进行探索；相反，我们强调了该领域正在进行和有希望研究的关键方面。

第三代神经网络主要使用“整合放电”（integrate-and-fire）型尖峰神经元，通过脉冲交换信息（图3）。第二代和第三代神经网络之间最大的区别在于信息处理性质。第二代神经网络使用了实值计算(real-value)（例如，信号振幅），而SNN则使用信号的时间（脉冲）处理信息。脉冲本质上是二进制事件，它或是0或是1。如图3a所示，SNNs中的神经元单元只有在接收或发出尖峰信号时才处于活跃状态，因此它是事件驱动型的，因此可以使其节省能耗。若无事件发生SNNs单元则保持闲置状态，这与DLNs相反。无论实值输入和输出，DLNs所有单位都处于活跃状态。此外，SNN中的输入值为1或0，这也减少了数学上的点积运算ΣiVi×wi（图3a），减小了求和的计算量。

针对不同的生物保真度水平下产生的脉冲代际，相关的尖峰神经元模型已被提出。例如泄漏整合放电型（LIF）（图3b）和霍奇金-赫克斯利型（Hodgkin–Huxley）。同样，针对于突触的可塑性，已有例如赫布型（Hebbian）和非赫布型（non-Hebbian）方案。突触的可塑性即突触权重的调节（在SNNs中转化为学习）取决于突触前和突触后尖峰的相对时间（图3c）。神经形态工程师的一个主要目标是：在利用基于事件（使用基于事件的传感器）及数据驱动更新的同时，建立一个具有适当突触可塑性的脉冲神经元模型，从而实现高效的识别、推理等智能应用。

我们认为，SNNs最大的优势在于其能够充分利用基于时空事件的信息。今天，我们有相当成熟的神经形态传感器，来记录环境实时的动态改变。这些动态感官数据可以与SNNs的时间处理能力相结合，以实现超低能耗的计算。实际上，与传统上DLNs使用的帧驱动（frame-driven）的方法相比，SNNs将时间作为附加的输入维度，以稀疏的方式记录了有价值的信息（图3），从而实现高效的SNNs框架，并通过计算视觉光流或立体视觉来实现深度感知。结合基于脉冲的学习规则，它可以产生有效的训练。机器人研究者已经证明使用基于事件的传感器进行跟踪和手势识别的优势。但是，这些应用程序大多数都使用了DLNs来执行识别。

在此类传感器中使用SNNs主要受限于缺乏适当的训练算法，从而可以有效地利用尖峰神经元的时间信息。实际上就精度而言，在大多数学习任务中SNNs的效果仍落后于第二代的深度学习。很明显，尖峰神经元可以实现非连续的信息传递，并发出不可微分的离散脉冲（见图3），因此它们不能使用基于梯度下降型的反向传播技术，而这是传统神经网络训练的基础。

另外，SNNs还受限于基于脉冲的数据可用性。虽然理想情况要求SNNs的输入是带有时间信息的序列，但SNNs训练算法的识别性能是在现有静态图像的数据集上进行评估的，例如CIFAR或ImageNet。然后，此类基于静态帧的数据将通过适当的编码技术（例如速率编码或次序编码，见图3d）转换为脉冲序列。虽然编码技术使我们能够评估SNNs在传统基准数据集上的性能，但我们要超越静态图像分类的任务。SNNs的最终能力应当来自于它们处理和感知瞬息万变的现实世界中的连续输入流，就像人脑轻而易举所做的那样。目前，我们既没有良好的基准数据集，也没有评估SNNs实际性能的指标。收集更多适当的基准数据集的研究，例如动态视觉传感器数据或驾驶和导航实例，便显得至关重要。

（这里我们指的是作为DLNs的第二代连续神经网络，以区别于基于脉冲的计算。我们注意到SNNs可以在具有卷积层次结构的深度架构上实现，并同时执行尖峰神经元功能。）

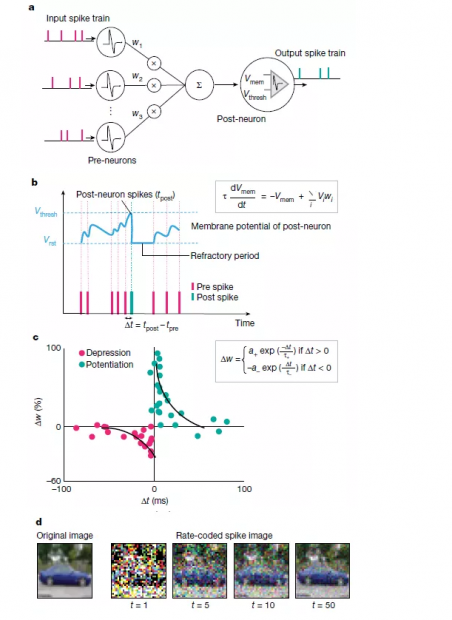
图3：SNN计算模型。a. 由输入上游神经元驱动的下游神经元组成的神经网络。上游神经尖峰Vi通过突触权重wi调节，在给点时间内产生合成电流ΣiVi×wi（相当于点积运算）。产生的合成电流会影响下游神经元的膜电位。B. LIF尖峰神经元的动力学显示。在没有脉冲的情况下，膜电位Vmem在时间常数τ中集成了传入脉冲和泄漏。当Vmem超过阈值Vthresh时，下游神经元输出脉冲。随之产生不应期，在此期间后神经元的Vmem不再受到影响。c，显示了基于实验数据的脉冲时间依赖的可塑性（STDP）公式，其中a +，a-，τ+和τ-是控制权重变化Δw的学习率和时间常数。突触权重wi根据上游神经元与下游神经元尖峰的时间差（Δt= tpost − tpre）更新。d，使用速率编码将输入图像（静态帧数据）转换为脉冲在各个时间步长上的映射。每个像素产生一个泊松脉冲序列，其激发速率与像素强度成正比。当几个时间步求和得出脉冲映射时（标记为t = 5的脉冲映射是从t = 1到t = 5的映射总和），它们开始类似于输入。因此，基于脉冲的编码既保留了输入图像的完整性，并且在时域中对数据进行了二值化。结果显示，LIF行为和随机输入尖峰的产生使SNN的内部动力学具有随机性。注意，序列编码也可以用来生成脉冲数据。

二、在SNNs中学习算法

基于转换的方法

这种方法的思路是获得一个SNN，对给定的任务，该SNN将产生与深度神经网络相同的输入输出映射。它的基本原理是，使用权重调整（weight rescaling）和归一化方法将训练有素的DLN转换为SNN，将非线性连续输出神经元的特征和尖峰神经元的泄漏时间常数（leak time constants），不应期（refractory period）、膜阈值（membrane threshold）等功能相匹配。

迄今为止，在图像分类的大型脉冲网络中（包括ImageNet数据集），这种方法能够产生了有竞争力的精确度。在基于转换的方法中，其优点是免除了时域中的训练负担。DLN使用了已有的深度学习框架例如Tensorflow对基于帧的数据进行训练，这些工具提供了训练中的灵活性。这种转换首先需要解析在基于事件的数据（通过对静态图像数据集进行速率编码获得）上进行训练的DLN，之后再进行简单的转换。

但是，这种方法有其内在的局限性。例如在使用双曲线正切（tanh）或归一化指数函数（softmax）后，非线性神经元的输出值可以得正也可以得负，而脉冲神经元的速率只能是正值。因此，负值总被丢弃，导致转换后的SNNs的精度下降。转换的另一个问题是在不造成严重的性能损失的前提下获得每一层最佳。最近的研究提出了确定最佳放电率的实用解决方案，以及在DLNs的训练过程中引入其他约束（例如噪音或泄漏修正线性单元（leaky ReLUs））以更好地匹配尖脉冲神经元的放电率。今天，转换的方法可为图像识别任务提供最先进的精度，并与DLNs的分类性能相当。值得注意的是，从DLNs转换的SNNs的推理时间变得很长（约几千个时间步长），导致延迟增加、能耗增加。

基于脉冲的方法

在基于脉冲的方法中，SNN使用时间信息进行训练，因此在整体脉冲动力学中具备明显的稀疏性和高效率优势。研究人员采用了两种主要方向：无监督学习（没有标记数据的训练），以及监督学习（有标记数据的训练）。早期监督学习成果是ReSuMe和tempotron，它们证明了在单层的SNN中，可以使用脉冲时间依赖的可塑性（STDP）的变体去进行分类。从那时起，研究工作一直致力于整合基于脉冲且类似于全局反向传播的误差梯度下降法，以便在多层SNNs中实现监督学习。大多数依赖反向传播的成果为脉冲神经元功能估计了一个近似可微的函数，从而使其能够执行梯度下降法（图4a）。SpikeProp及其相关变体已派生出通过在输出层固定一个目标脉冲序列来实现SNNs的反向传播规则。最近的成果对实值膜电位使用随机梯度下降法，是为了让正确输出神经元随机激发更多的脉冲（而不是具有精确目标的脉冲序列）。这些方法在深度卷积SNNs的小规模图像识别任务上取得了最新进展，例如美国国家标准与技术研究所（MNIST）手写数字数据库的数字分类。

然而，尽管计算效率更高，监督学习在大型任务的精度上无法超过基于转换的方法。另一方面，受到神经科学和硬件效率为主要目标的启发，基于STDP学习规则的局部无监督SNN训练也很有意思。通过局部学习（我们将在后面的硬件讨论中看到），有机会使记忆（突触存储）和计算（神经元输出）更紧密地相结合。这种架构更像人脑，也适合节能芯片上实现。Diehl等人率先证明了完全无监督的SNN学习，其精度可与 MNIST数据库深度学习相媲美（图4b）。

但是，将局部学习方法扩展到多层复杂任务是一个挑战。随着网络的深入，神经元的放电率会降低，我们称之为“消失的前向脉冲传播”。为了避免这种情况，多数工作用逐层的方式训练多层SNN（包括卷积SNNs）在局部的脉冲学习模式，然后进行全局学习反向传播学习，以去进行分类。这样局部和全局相结合的方法尽管很有成效，但在分类精度方面仍落后于转换的方法。此外，最近的成果显示了概念验证，即通过深度SNNs中反馈连接错误信号的随机投影确实有助于改善学习。这种基于反馈的学习方法需要进一步研究，以评估其在大规模任务上的效果。

对二元制学习的启示

我们可以通过仅用二进制（1/0）位值，而不是需要额外的内存的16位或32位浮点值来获得超低能耗和高效的计算。实际上在算法层级，目前正在研究以概率方式学习（关于神经元何时随机突跳，权重的转换精度何时变低）获得参数较少的网络和计算操作。二元和三元的DLNs也被提出，其神经元输出和权重只取低精度值-1、0和+1，而且在大规模分类任务中表现良好。基于二进制脉冲处理模式，SNN已具有计算优势。此外，LIF神经元的神经元动力学中的随机性可以顾及外部噪声（例如，有噪声的输入或有噪声权重的硬件参数），来提高网络的鲁棒性。那么，我们是否可以用结合此SNN时间处理架构使用适当的学习方法，并将权重训练压缩为二进制，使精度损失最小，还有待研究。

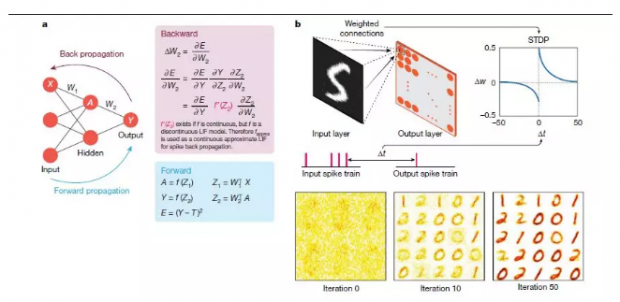
图4：尖峰网络中的全局和局部学习原理。a，在已知目标标签指导下进行全局学习，T用于分类任务。给定一个前馈网络，网络通过隐藏层单位A向前传播输入值X，并输出神经元激活值Y。结合非线性变换ƒ（Z1），使用输入的加权求和可以计算隐藏层的A，用矩阵符号表示为Z1 = W1 TX。输出以类似的方式进行计算。然后，用误差相对于权重（W1，W2）的导数E求出随后的权重更新。前向和反向传播的迭代导致学习。误差求导需要ƒ'，这要求ƒ'是连续的。因此，基于脉冲的反向传播的规则近似LIF函数可微方案。基于时间信息的处理细节没有显示在这里。b，局部STDP数字分类无监督学习。给定一个两层拓扑结构，输入层与输出层的所有神经元完全连接，通过STDP学习突触连接。根据输入层和输出层神经元的尖峰时间差异进行权重调整。输入神经元在输出之前（或之后）激发，权重值将增加（或减小）。随着迭代在多个时间步长上进行训练，权重在初始化时随机赋值，通过训练它将学习对一类输入所示的样式进行通用表示的编码（在这种情况下为“ 0”，“ 1”和“ 2”）。这里，为了进行识别，目标标签是不需要的。

三、其他有待研究的方向

超越视觉任务

到目前为止，我们已经给出了大多数分类任务处理的办法，那么如何处理在静态图像上识别和推理以外的任务呢？SNN也可以处理序列数据，但是并没有研究论证SNN在处理NLP的能力。使用SNN做因果推断的能力又如何呢？深度学习研究员在强化学习领域作出了大量的研究[62,63]，不过使用SNN进行强化学习研究的却很少。在SNN这一领域——特别是在训练学习算法中——SNN所面临的最大挑战就是否能表现出和深度学习相当的性能。尽管深度学习已经设下了很高的竞争门槛，但是我们相信SNN会在机器人、自主控制等领域表现的更好。

终身学习和小样本学习

深度学习模型在长期学习时会出现灾难性遗忘现象。比如，学习过任务A的神经网络在学习任务B时，它会忘记学过的任务A，只记得B。如何在动态的环境中像人一样具备长期学习的能力成为了学术界关注的热点。这固然是深度学习研究的一个新的方向，但我们应该探究给SNN增加额外的时间维度是否有助于实现持续性学习型任务。另一个类似的任务就是，利用少量数据进行学习，这也是SNN能超过深度学习的领域。SNN中的无监督学习可以与提供少量数据的监督学习相结合，只使用一小部分标记的训练数据得到高效的训练结果[ 46,50,65 ]。

与神经科学建立联系

我们可以和神经科学的研究成果相结合，把这些抽象的结果应用到学习规则中，以此提高学习效率。例如，Masquelier等人[65]利用STDP和时间编码模拟视觉神经皮层，他们发现不同的神经元能学习到不同的特征，这一点类似于卷积层学到不同的特征。研究者把树突学习[66]和结构可塑性[67]结合起来，把树突的连接数做为一个超参数，以此为学习提供更多的可能。SNN领域的一项互补研究是LSM（liquid state machines）[68]。LSM利用的是未经训练、随机链接的递归网络框架，该网络对序列识别任务表现卓著[ 69–71]。但是在复杂的大规模任务上的表现能力仍然有待提高。

四、硬件展望

从前文对信息处理能力和脉冲通信的描述中，我们容易假设一套具备类似能力的硬件系统。这套系统能够成为SNN的底层计算框架。受到在生物大脑中无处不在的神经元和突触的启发，设计出紧密结合在一起的计算和记忆结构；以及实现更复杂的功能——例如，使用最少的电路元件来模拟神经元与突触动力学。

神经形态计算的出现

在20世纪80年代，晶体管发明了40年后，在生物神经系统领域，Carver Mead设想了"更智能"、“更高效”的硅基计算机结构[72,73]。他也表示过自己最初试图建立神经系统的尝试是“简单而愚蠢的”[74]。但是他的工作代表了计算硬件领域的一种新的范式。Mead并不在意AND、OR等布尔运算[74]。相反他利用金属氧化物硅（MOS）晶体管在亚阈值区的电气物理特性（电压-电流指数相关）来模拟指数神经元的动力学特征[72]。这样的设备-通路协同设计是神经形态计算中最有趣的领域之一。

并行GPU的出现

和CPU这种由一个或者多个处理复杂任务的芯片组成的计算核心不同，GPU[75]是由多个可以进行并行计算的简单计算核心组成。因此能完成高并发、高吞吐的任务。在传统意义上GPU是加速图形应用程序的硬件加速器，但是现在有许多的非图形应用都受益于GPU的特性。深度学习就是一个显著的例子[6]，其实GPU不仅是深度神经网络的首选平台，也是SNN训练的平台[76,77]。虽然GPU在高扩展性上具备优势，但无法很好的用来进行基于事件驱动的脉冲计算。因此，事件驱动的“超级大脑”神经芯片就可以提供高效的解决方案[78,79]。

“超级大脑”芯片

“超级大脑”芯片[80]的特点是整合了百万计的神经元和突触，神经元和突触提供了脉冲计算的能力[78,81–86]。Neurogrid[82]和TrueNorth[84]分别是基于混合信号模拟电路和数字电路的两种模型芯片。Neurogrid使用数字电路，因为模拟电路容易积累错误，且芯片制造过程中的错误影响也较大。设计神经网络旨在帮助科学家模拟大脑活动，通过复杂的神经元运作机制——比如离子通道的开启和关闭，以及突触特有的生物行为[82,87]。相比而言，TrueNorth作为一款神经芯片，目的是用于重要商业任务，例如使用SNN分类识别任务；而且TrueNorth是基于简化的神经科突触原型来设计的。

以TrueNorth为例，主要特性如下[78,88]：

异步地址事件表示（Asynchronous address event representation）：首先，异步地址事件表示不同于传统的芯片设计，在传统的芯片设计中，所有的计算都按照全局时钟进行，但是因为SNN是稀疏的，仅当脉冲产生时才要进行计算，所以异步事件驱动的计算模式更加适合进行脉冲计算[89,90]。

芯片网络：芯片网络（networks-on-chip，NOCs）可以用于脉冲通信，NOC就是芯片上的路由器网络，通过时分复用技术用总线收发数据包。大规模芯片必须使用NOC，是因为在硅片加工的过程中，连接主要是二维的，在第三个维度灵活程度有限。也要注意到，尽管使用了NOC但芯片的联通程度，仍然不能和大脑中的三维连通性相比。包括TrueNorth在内的大规模数字神经芯片，比如Loihi[78]，已经展示除了SNN技术以外的应用效果。使得我们能更加接近生物仿真技术。不过，有限的连通性，NOC总线带宽的限制，和全数字方法仍然需要进一步的研究。

超越冯·诺依曼式计算

晶体管尺寸规模的持续行缩小的现象被称之为摩尔定律[91]，摩尔定律推动了CPU和GPU以及“超级大脑”芯片的不断发展。不过近些年，随着硅基晶体管接近物理极限，这一发展速度放缓[92]。为了适应现代人类对计算能力的不断提升，研究者们设计出了一种双管齐下的方法，使得“超冯·诺依曼”、“超硅”计算模型成为了可能，冯·诺依曼模型的一大特征就是，存储单元和运算单元的分离[93]。通过系统总线传输数据。因此，数据在高速的运算单元和低速的存储单元之间的频繁传输就成为了众所周知的“存储墙瓶颈”（memory wall bottleneck）。这一瓶颈限制了计算的吞吐和效率[94]。

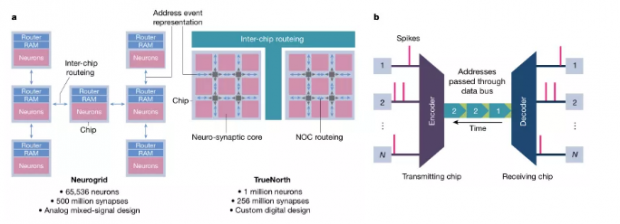
图5：一些有代表性的“超级大脑”芯片和AER方法

A，Neurogrid拥有65,000多个神经元和5亿个突触，而TrueNorth拥有100万神经元和2.56亿个突触。Neurogrid和TrueNorth分别使用树和网格路由拓扑两种结构。Neurogrid使用模拟混合信号设计，TrueNorth依赖数字基元。一般来说，像TrueNorth 这样的数字神经形态系统将神经元的膜电位表示为n位二进制格式。通过适当增加或减少n位字来实现神经元动力学，比如LIF行为。相比之下，模拟系统将膜电位表示为存储在电容中的电荷。通过电流从电容进出，模拟所需的神经元动力学。尽管存在电路差异，但一般来说，模拟系统和数字系统都使用事件驱动AER进行尖峰通信。事件驱动通信是实现低能耗大规模集成系统的关键。B，基本的 AER通信系统。每当发射端送出一个事件（一个脉冲），相应的地址就通过数据总线发送到接收端。接收端解码输入地址，并重新构造脉冲的序列。因此，每个脉冲由其位置（地址）显式编码，并在其地址发送到数据总线时隐式编码。

减轻这一瓶颈影响的方法就是使用“近内存（near-memory）”、“内存中”计算[95,96]。近内存计算是通过在内存单元附近嵌入一个专门的处理器，由此实现内存和计算的“共存”。实际上，各种“超级大脑芯片”的分布式计算体系结构所具有的紧密放置的神经元和突触阵列就是近内存计算的表现。相比较而言，内存中计算则是把部分计算操作嵌入到内存内部或外部电路中。

非易失性技术

非易失性技术（ non-volatile technology）[97–103]通常被用于与生物突触相比较。实际上，它们展示了生物突触的两个特征：突触效能（synaptic efficacy）和突触可塑性（ synaptic plasticity）。突触可塑性指的是根据特定的学习规则调整突触权重的能力。突触效能指的是根据输入脉冲产生输出的现象。以最简单的形式来说，意思就是，输入的脉冲信号乘以突触的权重。这表示着可编程、模拟、非易失性。从上游神经元得到的信号，相乘再求和后再作用于下游神经元的输入。后文的图片就说明了，如何使用新兴的非易失性忆阻技术（ non-volatile memristive technology）实现突触效率和突触可塑性[103,104]。而且，还可以通过时间驱动NOC的方式了连接开关，从而构建密集大规模的神经处理器，以实现内存中计算。

一些已经发表过的基于忆阻技术的研究[105,106]，比如可变电阻式内存（RRAM）[107]、相变内存（PCM）[108]、和自旋传递扭矩磁性随机读写存储器（STT-MRAM）[109]，已经在原位点积和基于 STDP 规则的突触学习中进行了探索。RRAM（氧化物基和导电桥基[107]）是电场驱动器件，依靠丝极的形成来模拟可编程电阻。RRAM容易出现因设备、因周期的变化[110,111]，这是这一技术的主要障碍。PCMS包括夹在两个电极之间的硫系材料，可以在非晶态（高电阻）和晶态（低电阻）之间转换。PCM设备有类似的编程电压和RRAM的写入速度，不过这种器件也会受到高写入电流和长时间电阻漂移的影响[108]。自旋电子器件是由两块垫片隔开的磁铁组成，依据两层的磁化方向是平行还是反平行，能呈现两种电磁状态。与RRAM和PCM相比，自旋装置显示出几乎无限的耐久性，更低的写入能量和更快的磁极反转速度[109]。然而，在自旋器件中，两个极端电阻态（ON/OFF）的比率要比在PCM和RRAM中小得多。

另一类包含可调非易失性电阻的非易失性器件是浮栅晶体管（floating-gate transistor）。此类设备有作为突触存储器的潜力[112–114]。实际上浮栅晶体管是第一个用作非易失性突触存储器的设备[115,116]。因为，他们与MOS制造工艺的相容，比其他新型器件的生产技术更加成熟，然而，与其他非易失性技术相比，浮栅晶体管的主要缺点是耐用性低和编程电压高。

虽然原位计算（situ computing）和突触学习为大规模超越冯·诺依曼分布式计算提供了诱人的前景，但有许多的挑战仍然有待克服，因设备、因周期和进程相关引起的变化，计算的近似性质容易出现错误，从而减低整体的计算效率，最终影响准确性。此外，交叉开关操作的鲁棒性受到电流潜通路、线电阻、驱动电路的源电阻和感测电阻的存在的影响[117,118]。选择器（晶体管或双端非线性装置）的非理想性、对模拟-数字转换设备的要求和有限的比特精度要求，也增加了使用非传统突触装置设计可靠计算的总体复杂性。此外，写入非易失性设备通常会消耗大量的资源。而且，此类设备的固有随机性会导致不可靠的写操作，又需要代价高昂的检验方案[119]。

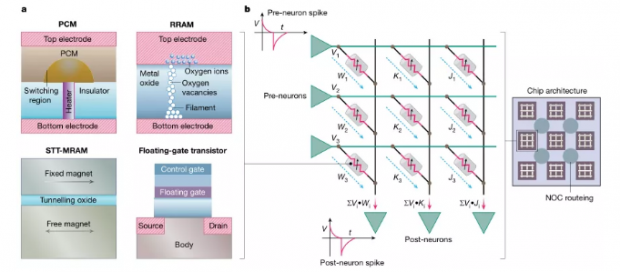
图6：使用非易失性存储设备作为突触存储器件。

A，各种非易失性技术的原理图：PCM，RRAM，STT-MRAM和浮栅晶体管。这种非易失性设备已经被用作突触存储和原位神经突触计算，以及通用非神经形态存储器内加速器。B，用忆阻技术实现突触效能和突触可塑性。图中展示了以交叉方式连接的忆阻器阵列。根据欧姆定律，水平线（绿色）上的输入脉冲产生与忆阻元件电导成比例的电流。又因为基尔霍夫电流定律，与通过多个峰前神经元的电流沿着垂直线（黑色）相加。这一操作表示了具备突触功效的内存中点积运算。通常，只要神经元前和后尖峰分别在水平线和垂直线上(如在STDP)，突触可塑性就可以通过适当地施加电压脉冲来原位实现。组成忆阻器的电阻值是根据在相应的水平和垂直线上产生的电压差编程的。根据特定的器件技术，再选择要编程电压脉冲的形状和定时。请注意，浮栅晶体管是三端子器件，因此需要额外的水平线和（或）垂直线来实现交叉开关功能。该图还显示了以平铺方式连接NOC的忆阻阵列，由此可以实现高吞吐量的原位计算。

硅（内存中）计算

除了非易失性技术之外，各种使用标准硅存储器（包括静态和动态随机存取存储器）进行内存计算的设想均在研究中。这些工作主要集中在把布尔向量计算嵌入内存数组中[120–122]。此外，混合信号模拟内存计算操作和二进制卷积操作最近被证明是可行的[123,124]。事实上，目前几乎所有主要的内存技术都在探索各种形式的内存计算，包括静态内存[125]和动态内存[126]、RRAM[127]、PCM[128]和STT-MRAM[129]。尽管这些工作大部分集中在常见的计算应用上，如加密和深度神经网络，但他们也可以轻松的一直到SNN上来。

五、算法-硬件协同设计

混合信号模拟计算

模拟计算容易受到过程引起的变化和噪声的影响，并且由于模拟和数字转换设备的复杂性和精度要求，在面积和能耗方面就受到了很大限制。将芯片学习与紧密结合的模拟计算框架相结合，将使这类系统能够从根本上适应过程引起的变化，从而减轻对精度的影响。在过去[130,131]以及近期的可行性生物算法的研究[54]中，已经研究了以芯片上（ on-chip）和设备上（on-device）学习解决方案为重点的局部学习。本质上，无论是局部学习这种形式还是树突学习这种范式，我们都认为，更好的容错局部学习算法——即使是要学习额外的参数——将是推动模拟神经形态计算的关键所在。此外，芯片上学习的适应能力可在不降低目标精度的前提下，开发低成本的近似模数转换器。

忆阻点积

作为模拟计算的一个实例，忆阻点积（Memristive dot products）是实现原位神经形态计算的一种有前景的方法。不幸的是，表示点积的忆阻阵列中产生的电流既有空间依赖性又有数据依赖性，这使得交叉开关电路分析成为一个非常复杂的问题。研究交叉开关电路非理想状态的影响[117,132,133]，探索减轻点积不准确影响的训练方法的研究并不多[118,134]。而且，这些工作大部分集中在深度神经网络而不是SNN中。然而，我们可以合理地假设，在这些工作中开发出的基本器件和对电路的见解也能用于SNN的实现。现有的工作需要精致的的设备-通路模拟运行，必须与训练算法紧密耦合，以减少精度损失。我们认为，基于最新设备的交叉开关阵列的理论模型，以及为点积误差建立理论边界的努力，都将引起人们的关注。这将使算法设计者无需耗时、设计迭代设备-通路-算法模拟，就能探索新的训练算法，同时也能解决硬件不一致的问题。

随机性

随机SNN引起了人们极大的兴趣，这是因为新兴的设备本身具有随机性[135,136]。随机二进制SNN 的实现结果，大多数都集中在MNIST数字识别之类的小规模任务上[56]。这类工作的共同主题是使用随机STDP类的本地学习规则来生成权重更新。我们认为，即使在二元条件下，STDP学习中的时间维度权重更新提供了额外的带宽，是的整体朝着真确的方向前进（总体精度）。这种二元局部学习方案与基于梯度下降的大规模学习规则相结合，在利用了硬件随机性的同时，为高能效神经系统提供了有利的机会。

混合设计方法

我们认为，基于混合方法的硬件解决方案——即在单一平台上结合各种技术的优势——是另一个需要深入研究的重要领域。这种方法可以在最近的文献中找到[137]，比如，把低精度忆阻器与高精度数字处理器结合使用。这种混合方法有许多可能的变体，包括显著驱动的计算数据分离、混合精度计算[137]、将常规硅存储器重新配置为需内存近似加速器[125]、局部同步和全局异步设计[138]、局部模拟和全局数字系统；其中新兴技术和传统技术可以同时使用，以提高精确度和效率。此外，这种混合硬件可以与基于混合脉冲学习的方法结合使用，例如局部无监督学习，然后是全局有监督反向传播算法[53]。我们认为，这种局部-全局学习方案可以用来降低硬件复杂性，同时，最大限度的减少对终端应用程序的性能影响。

六、总结

如今，“智能化”已经成为了我们周围所有学科的主题。在这方面，本文阐述了神经形态计算作为一种高效方式，通过硬件（计算）和算法（智能）的协同演化的方式来实现机器智能。

我们首先讨论了脉冲神经范式的算法含义，这种范式使用事件驱动计算，而不是传统深度学习范式中的数值计算。描述了实现标准分类任务的学习规则（例如基于脉冲的梯度下降、无监督STDP和从深度学习到脉冲模型的转换方法）的优点和局限性。

未来的算法研究应该利用基于脉冲信号的信息处理的稀疏和时间动态特性；以及可以产生实时识别的互补神经形态学数据集；硬件开发应该侧重于事件驱动的计算、内存和计算单元的协调，以及模拟神经突触的动态特征。特别引人关注的是新兴的非易失性技术，这项技术支持了原位混合信号的模拟计算。我们也讨论了包含算法-硬件协同设计的跨层优化的前景。例如，利用算法适应性（局部学习）和硬件可行性（实现随机脉冲）。

最后，我们谈到，基于传统和新兴设备构建的基于脉冲的节能智能系统与当前无处不在的人工智能相比，二者的前景其实是相吻合的。现在是我们该交换理念的时候了，通过设备、通路、架构和算法等多学科的努力，通力合作打造一台真正节能且智能的机器。

参考文献

1. Silver, D. et al. Mastering the game of Go without human knowledge. Nature 550, 354–359 (2017).

2. Cox, D. D. & Dean, T. Neural networks and neuroscience-inspired computer vision. Curr. Biol. 24, R921–R929 (2014).

3. Milakov, M. Deep Learning With GPUs.

https://www.nvidia.co.uk/docs/IO/147844/Deep-Learning-With-GPUs-MaximMilakov-NVIDIA.pdf (Nvidia, 2014).

Am. Sociol. Rev. 80, –908 (2015). 875doi: 10.1177/0003122415601618

4. Bullmore, E. & Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci. 13, 336–349 (2012).

5. Felleman, D. J. & Van Essen, D. C. Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47 (1991).

6. Krizhevsky, A., Sutskever, I. & Hinton, G. E. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems Vol. 28 (eds Pereira, F. et al.) 1097–1105 (Neural Information Processing Systems Foundation, 2012). This work—using deep convolutional networks—was the first to win the ImageNet challenge, fuelling the subsequent deep-learning revolution.

7. Deco, G., Rolls, E. T. & Romo, R. Stochastic dynamics as a principle of brain function. Prog. Neurobiol. 88, 1–16 (2009).

8. Venkataramani, S., Roy, K. & Raghunathan, A. Efficient embedded learning for IoT devices. In 21st Asia and South Pacific Design Automation Conf. 308–311 (IEEE, 2016).

9. Maass, W. Networks of spiking neurons: the third generation of neural network models. Neural Netw. 10, 1659–1671 (1997). This paper was one of the first works to provide a rigorous mathematical analysis of the computational power of spiking neurons, categorizing them as the third generation of neural networks (after perceptron and sigmoidal neurons).

10. McCulloch, W. S. & Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5, 115–133 (1943).

11. Nair, V. & Hinton, G. E. Rectified linear units improve restricted Boltzmann machines. In Proc. 27th Int. Conf. on Machine Learning (eds Fürnkranz, J. & Joachims, T.) 807–814 (IMLS, 2010)

doi: 10.1038/srep01069; pmid: 23323212

12. Rumelhart, D. E., Hinton, G. E. & Williams, R. J. Learning representations by back-propagating errors. Nature 323, 533–536 (1986). This seminal work proposed gradient-descent-based backpropagation as a learning method for neural networks.

13. Izhikevich, E. M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572 (2003).

14. Hebb, D. O. The Organization of Behavior: A Neuropsychological Theory (Wiley, 1949).

15. Abbott, L. F. & Nelson, S. B. Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183 (2000).

16. Liu, S.-C. & Delbruck, T. Neuromorphic sensory systems. Curr. Opin. Neurobiol. 20, 288–295 (2010).

17. Lichtsteiner, P., Posch, C. & Delbruck, T. A. 128×128 120 db 15 μs latency asynchronous temporal contrast vision sensor. IEEE J. Solid-State Circuits 43, 566–576 (2008).

18. Vanarse, A., Osseiran, A. & Rassau, A. A review of current neuromorphic approaches for vision, auditory, and olfactory sensors. Front. Neurosci. 10, 115 (2016).

19. Benosman, R., Ieng, S.-H., Clercq, C., Bartolozzi, C. & Srinivasan, M. Asynchronous frameless event-based optical flow. Neural Netw. 27, 32–37 (2012).

20. Wongsuphasawat, K. & Gotz, D. Exploring flow, factors, and outcomes of temporal event sequences with the outflow visualization. IEEE Trans. Vis. Comput. Graph. 18, 2659–2668 (2012).

21. Rogister, P., Benosman, R., Ieng, S.-H., Lichtsteiner, P. & Delbruck, T. Asynchronous event-based binocular stereo matching. IEEE Trans. Neural Netw. Learn. Syst. 23, 347–353 (2012).

22. Osswald, M., Ieng, S.-H., Benosman, R. & Indiveri, G. A spiking neural network model of 3D perception for event-based neuromorphic stereo vision systems. Sci. Rep. 7, 40703 (2017).

23. Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R. R. Improving neural networks by preventing co-adaptation of feature detectors. Preprint at http://arxiv.org/abs/1207.0580 (2012).

24. Deng, J. et al. ImageNet: a large-scale hierarchical image database. In IEEE Conf. on Computer Vision and Pattern Recognition 248–255 (IEEE, 2009).

25. Rullen, R. V. & Thorpe, S. J. Rate coding versus temporal order coding: what the retinal ganglion cells tell the visual cortex. Neural Comput. 13, 1255–1283 (2001).

26. Hu, Y., Liu, H., Pfeiffer, M. & Delbruck, T. DVS benchmark datasets for object tracking, action recognition, and object recognition. Front. Neurosci. 10, 405 (2016).

27. Geiger, A., Lenz, P., Stiller, C. & Urtasun, R. Vision meets robotics: the KITTI dataset. Int. J. Robot. Res. 32, 1231–1237 (2013).

28.Barranco, F., Fermuller, C., Aloimonos, Y. & Delbruck, T. A dataset for visual navigation with neuromorphic methods. Front. Neurosci. 10, 49 (2016).

29.Sengupta, A., Ye, Y., Wang, R., Liu, C. & Roy, K. Going deeper in spiking neural networks: VGG and residual architectures. Front. Neurosci. 13, 95 (2019). This paper was the first to demonstrate the competitive performance of a conversion-based spiking neural network on ImageNet data for deep neural architectures.

30.Cao, Y., Chen, Y. & Khosla, D. Spiking deep convolutional neural networks for energy-efficient object recognition. Int. J. Comput. Vis. 113, 54–66 (2015).

31.Diehl, P. U. et al. Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing. In Int. Joint Conf. on Neural Networks 2933–2341 (IEEE, 2015).

32.Pérez-Carrasco, J. A. et al. Mapping from frame-driven to frame-free event-driven vision systems by low-rate rate coding and coincidence processing—application to feedforward ConvNets. IEEE Trans. Pattern Anal. Mach. Intell. 35, 2706–2719 (2013).

33.Rueckauer, B., Lungu, I.-A., Hu, Y., Pfeiffer, M. & Liu, S.-C. Conversion of continuous-valued deep networks to efficient event-driven networks for image classification. Front. Neurosci. 11, 682 (2017).

34.Diehl, P. U., Zarrella, G., sidy, A. S., Pedroni, B. U. & Neftci, E. Conversion of artificial recurrent neural networks to spiking neural networks for low-power neuromorphic hardware. In Int. Conf. on Rebooting Computing 20 (IEEE, 2016).

35.Abadi, M. et al. Tensorflow: a system for large-scale machine learning. In 12th USENIX Symp. Operating Systems Design and Implementation 265–283 (2016).

36.Hunsberger, E. & Eliasmith, C. Spiking deep networks with LIF neurons. Preprint at http://arxiv.org/abs/1510.08829 (2015)

37.Pfeiffer, M. & Pfeil, T. Deep learning with spiking neurons: opportunities and challenges. Front. Neurosci. 12, 774 (2018).

38.Ponulak, F. & Kasiński, A. Supervised learning in spiking neural networks with ReSuMe: sequence learning, classification, and spike shifting. Neural Comput. 22, 467–510 (2010).

39.Gütig, R. & Sompolinsky, H. The tempotron: a neuron that learns spike-timing-based decisions. Nat. Neurosci. 9, 420–428 (2006).

40.Bohte, S. M., Kok, J. N. & La Poutré, H. Error-backpropagation in temporally encoded networks of spiking neurons. Neurocomputing 48, 17–37 (2002).

41.Ghosh-Dastidar, S. & Adeli, H. A new supervised learning algorithm for multiple spiking neural networks with application in epilepsy and seizure detection. Neural Netw. 22, 1419–1431 (2009).

42.Anwani, N. & Rajendran, B. NormAD: normalized approximate descent-based supervised learning rule for spiking neurons. In Int. Joint Conf. on Neural Networks 2361–2368 (IEEE, 2015).

43.Lee, J. H., Delbruck, T. & Pfeiffer, M. Training deep spiking neural networks using backpropagation. Front. Neurosci. 10, 508 (2016).

44.Orchard, G. et al. HFirst: a temporal approach to object recognition. IEEE Trans. Pattern Anal. Mach. Intell. 37, 2028–2040 (2015).

45.Mostafa, H. Supervised learning based on temporal coding in spiking neural networks. IEEE Trans. Neural Netw. Learn. Syst. 29, 3227–3235 (2018).

46.Panda, P. & Roy, K. Unsupervised regenerative learning of hierarchical features in spiking deep networks for object recognition. In Int. Joint Conf. on Neural Networks 299–306 (IEEE, 2016).

47.LeCun, Y., Cortes, C. & Burges, C. J. C. The MNIST Database of Handwritten Digits http://yann.lecun.com/exdb/mnist/ (1998).

48.Masquelier, T., Guyonneau, R. & Thorpe, S. J. Competitive STDP-based spike pattern learning. Neural Comput. 21, 1259–1276 (2009).

49.Diehl, P. U. & Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Front. Comput. Neurosci. 9, 99 (2015). This is a good introduction to implementing spiking neural networks with unsupervised STDP-based learning for real-world tasks such as digit recognition.

50.Kheradpisheh, S. R., Ganjtabesh, M., Thorpe, S. J. & Masquelier, T. STDP-based spiking deep convolutional neural networks for object recognition. Neural Netw. 99, 56–67 (2018).

51.Neftci, E., Das, S., Pedroni, B., Kreutz-Delgado, K. & Cauwenberghs, G. Event-driven contrastive divergence for spiking neuromorphic systems. Front. Neurosci. 7, 272 (2014).

52.Stromatias, E., Soto, M., Serrano-Gotarredona, T. & Linares-Barranco, B. An event-driven classifier for spiking neural networks fed with synthetic or dynamic vision sensor data. Front. Neurosci. 11, 350 (2017).

53.Lee, C., Panda, P., Srinivasan, G. & Roy, K. Training deep spiking convolutional neural networks with STDP-based unsupervised pre-training followed by supervised fine-tuning. Front. Neurosci. 12, 435 (2018).

54.Mostafa, H., Ramesh, V. & Cauwenberghs, G. Deep supervised learning using local errors. Front. Neurosci. 12, 608 (2018).

55.Neftci, E. O., Augustine, C., Paul, S. & Detorakis, G. Event-driven random back-propagation: enabling neuromorphic deep learning machines. Front. Neurosci. 11, 324 (2017).

56.Srinivasan, G., Sengupta, A. & Roy, K. Magnetic tunnel junction based long-term short-term stochastic synapse for a spiking neural network with on-chip STDP learning. Sci. Rep. 6, 29545 (2016).

57.Tavanaei, A., Masquelier, T. & Maida, A. S. Acquisition of visual features through probabilistic spike-timing-dependent plasticity. In Int. Joint Conf. on Neural Networks 307–314 (IEEE, 2016).

58.Bagheri, A., Simeone, O. & Rajendran, B. Training probabilistic spiking neural networks with first-to-spike decoding. In Int. Conf. on Acoustics, Speech and Signal Processing 2986–2990 (IEEE, 2018).

59.Rastegari, M., Ordonez, V., Redmon, J. & Farhadi, A. XNOR-Net: ImageNet classification using binary convolutional neural networks. In Eur. Conf. on Computer Vision 525–542 (Springer, 2016).

60.Courbariaux, M., Bengio, Y. & David, J.-P. BinaryConnect: training deep neural networks with binary weights during propagations. In Advances in Neural Information Processing Systems Vol. 28 (eds Cortes, C. et al) 3123–3131 (Neural Information Processing Systems Foundation, 2015).

61.Stromatias, E. et al. Robustness of spiking deep belief networks to noise and reduced bit precision of neuro-inspired hardware platforms. Front. Neurosci. 9, 222 (2015).

62.Florian, R. V. Reinforcement learning through modulation of spike-timing-dependent synaptic plasticity. Neural Comput. 19, 1468–1502 (2007).

63.Vasilaki, E., Frémaux, N., Urbanczik, R., Senn, W. & Gerstner, W. Spike-based reinforcement learning in continuous state and action space: when policy gradient methods fail. PLOS Comput. Biol. 5, e1000586 (2009).

64.Zuo, F. et al. Habituation-based synaptic plasticity and organismic learning in a quantum perovskite. Nat. Commun. 8, 240 (2017).

65.Masquelier, T. & Thorpe, S. J. Unsupervised learning of visual features through spike-timing-dependent plasticity. PLOS Comput. Biol. 3, e31 (2007).

ADS

66.Rao, R. P. & Sejnowski, T. J. Spike-timing-dependent Hebbian plasticity as temporal difference learning. Neural Comput. 13, 2221–2237 (2001).

67.Roy, S. & Basu, A. An online unsupervised structural plasticity algorithm for spiking neural networks. IEEE Trans. Neural Netw. Learn. Syst. 28, 900–910 (2017).

68.Maass, W. Liquid state machines: motivation, theory, and applications. In Computability in Context: Computation and Logic in the Real World (eds Cooper, S. B. & Sorbi, A.) 275–296 (Imperial College Press, 2011).

69.Schrauwen, B., D’Haene, M., Verstraeten, D. & Van Campenhout, J. Compact hardware liquid state machines on FPGA for real-time speech recognition. Neural Netw. 21, 511–523 (2008).

70.Verstraeten, D., Schrauwen, B., Stroobandt, D. & Van Campenhout, J. Isolated word recognition with the liquid state machine: a e study. Inf. Process. Lett. 95, 521–528 (2005).

71.Panda, P. & Roy, K. Learning to generate sequences with combination of Hebbian and non-Hebbian plasticity in recurrent spiking neural networks. Front. Neurosci. 11, 693 (2017).

72.Maher, M. A. C., Deweerth, S. P., Mahowald, M. A. & Mead, C. A. Implementing neural architectures using analog VLSI circuits. IEEE Trans. Circ. Syst. 36, 643–652 (1989).

73.Mead, C. Neuromorphic electronic systems. Proc. IEEE 78, 1629–1636 (1990). This seminal work established neuromorphic electronic systems as a new paradigm in hardware computing and highlights Mead’s vision of going beyond the precise and well defined nature of digital computing towards brain-like aspects.

74.Mead, C. A. Neural hardware for vision. Eng. Sci. 50, 2–7 (1987).

75.NVIDIA Launches the World’s First Graphics Processing Unit GeForce 256. https://www.nvidia.com/object/IO_20020111_5424.html (Nvidia, 1999).

76.Nageswaran, J. M., Dutt, N., Krichmar, J. L., Nicolau, A. & Veidenbaum, A. V. A configurable simulation environment for the efficient simulation of large-scale spiking neural networks on graphics processors. Neural Netw. 22, 791–800 (2009).

77.Fidjeland, A. K. & Shanahan, M. P. Accelerated simulation of spiking neural networks using GPUs. In Int. Joint. Conf. on Neural Networks 3041–3048 (IEEE, 2010).

78.Davies, M. et al. Loihi: a neuromorphic manycore processor with on-chip learning. IEEE Micro 38, 82–99 (2018).

79.Blouw, P., Choo, X., Hunsberger, E. & Eliasmith, C. Benchmarking keyword spotting efficiency on neuromorphic hardware. In Proc. 7th Annu. Neuro-inspired Computational Elements Workshop 1 (ACM, 2018).

80.Hsu, J. How IBM got brainlike efficiency from the TrueNorth chip. IEEE Spectrum https://spectrum.ieee.org/computing/hardware/how-ibm-got-brainlike-efficiency-from-the-truenorth-chip (29 September 2014).

81.Khan, M. M. et al. SpiNNaker: mapping neural networks onto a massively parallel chip multiprocessor. In Int. Joint Conf. on Neural Networks 2849–2856 (IEEE, 2008). This was one of the first works to implement a large-scale spiking neural network on hardware using event-driven computations and commercial processors.

82.Benjamin, B. V. et al. Neurogrid: a mixed-analog–digital multichip system for large-scale neural simulations. Proc. IEEE 102, 699–716 (2014).

83.Schemmel, J. et al. A wafer-scale neuromorphic hardware system for large-scale neural modeling. In Int. Symp. Circuits and Systems 1947–1950 (IEEE, 2010).

84.Merolla, P. A. et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 345, 668–673 (2014). This work describes TrueNorth, the first digital custom-designed, large-scale neuromorphic processor, an outcome of the DARPA SyNAPSE programme; it was geared towards solving commercial applications through a digital neuromorphic implementation.

85.Furber, S. Large-scale neuromorphic computing systems. J. Neural Eng. 13, 051001 (2016).

86.Qiao, N. et al. A reconfigurable on-line learning spiking neuromorphic processor comprising 256 neurons and 128k synapses. Front. Neurosci. 9, 141 (2015).

87.Indiveri, G. et al. Neuromorphic silicon neuron circuits. Front. Neurosci. 5, 73 (2011).

88.Seo, J.-s. et al. A 45 nm CMOS neuromorphic chip with a scalable architecture for learning in networks of spiking neurons. In Custom Integrated Circuits Conf. 311–334 (IEEE, 2011).

89.Boahen, K. A. Point-to-point connectivity between neuromorphic chips using address events. IEEE Trans. Circuits Syst. II 47, 416–434 (2000). This paper describes the fundamentals of address event representation and its application to neuromorphic systems.

90.Serrano-Gotarredona, R. et al. AER building blocks for multi-layer multi-chip neuromorphic vision systems. In Advances in Neural Information Processing Systems Vol. 18 (eds Weiss, Y., Schölkopf, B. & Platt, J. C.) 1217–1224 (Neural Information Processing Systems Foundation, 2006).

91.Moore, G. E. Cramming more components onto integrated circuits. Proc. IEEE 86, 82–85 (1998).

92.Waldrop, M. M. The chips are down for Moore’s law. Nature 530, 144 (2016).

93.von Neumann, J. First draft of a report on the EDVAC. IEEE Ann. Hist. Comput. 15, 27–75 (1993).

94.Mahapatra, N. R. & Venkatrao, B. The processor–memory bottleneck: problems and solutions. Crossroads 5, 2 (1999).

95.Gokhale, M., Holmes, B. & Iobst, K. Processing in memory: the Terasys massively parallel PIM array. Computer 28, 23–31 (1995).

96.Elliott, D., Stumm, M., Snelgrove, W. M., Cojocaru, C. & McKenzie, R. Computational RAM: implementing processors in memory. IEEE Des. Test Comput. 16, 32–41 (1999).

97.Ankit, A., Sengupta, A., Panda, P. & Roy, K. RESPARC: a reconfigurable and energy-efficient architecture with memristive crossbars for deep spiking neural networks. In Proc. 54th ACM/EDAC/IEEE Annual Design Automation Conf. 63.2 (IEEE, 2017).

98.Bez, R. & Pirovano, A. Non-volatile memory technologies: emerging concepts and new materials. Mater. Sci. Semicond. Process. 7, 349–355 (2004).

99.Xue, C. J. et al. Emerging non-volatile memories: opportunities and challenges. In Proc. 9th Int. Conf. on Hardware/Software Codesign and System Synthesis 325–334 (IEEE, 2011).

100.Wong, H.-S. P. & Salahuddin, S. Memory leads the way to better computing. Nat. Nanotechnol. 10, 191 (2015); correction 10, 660 (2015).

101.Chi, P. et al. Prime: a novel processing-in-memory architecture for neural network computation in ReRAM-based main memory. In Proc. 43rd Int. Symp. Computer Architecture 27–39 (IEEE, 2016).

102.Shafiee, A. et al. ISAAC: a convolutional neural network accelerator with in-situ analog arithmetic in crossbars. In Proc. 43rd Int. Symp. Computer Architecture 14–26 (IEEE, 2016).

103.Burr, G. W. et al. Neuromorphic computing using non-volatile memory. Adv. Phys. X 2, 89–124 (2017).

104.Snider, G. S. Spike-timing-dependent learning in memristive nanodevices. In Proc. Int. Symp. on Nanoscale Architectures 85–92 (IEEE, 2008).

105.Chua, L. Memristor—the missing circuit element. IEEE Trans. Circuit Theory 18, 507–519 (1971). This was the first work to conceptualize memristors as fundamental passive circuit elements; they are currently being investigated as high-density storage devices through various emerging technologies for conventional general-purpose and neuromorphic computing architectures.

106.Strukov, D. B., Snider, G. S., Stewart, D. R. & Williams, R. S. The missing memristor found. Nature 453, 80–83 (2008).

107.Waser, R., Dittmann, R., Staikov, G. & Szot, K. Redox-based resistive switching memories—nanoionic mechanisms, prospects, and challenges. Adv. Mater. 21, 2632–2663 (2009).

108.Burr, G. W. et al. Recent progress in phase-change memory technology. IEEE J. Em. Sel. Top. Circuits Syst. 6, 146–162 (2016).

109.Hosomi, M. et al. A novel nonvolatile memory with spin torque transfer magnetization switching: spin-RAM. In Int. Electron Devices Meeting 459–462 (IEEE, 2005).

110.Ambrogio, S. et al. Statistical fluctuations in HfOx resistive-switching memory. Part I—set/reset variability. IEEE Trans. Electron Dev. 61, 2912–2919 (2014).

111.Fantini, A. et al. Intrinsic switching variability in HfO2 RRAM. In 5th Int. Memory Workshop 30–33 (IEEE, 2013).

112.Merrikh-Bayat, F. et al. High-performance mixed-signal neurocomputing with nanoscale floating-gate memory cell arrays. IEEE Trans. Neural Netw. Learn. Syst. 29, 4782–4790 (2017).

113.Ramakrishnan, S., Hasler, P. E. & Gordon, C. Floating-gate synapses with spike-time-dependent plasticity. IEEE Trans. Biomed. Circuits Syst. 5, 244–252 (2011).

114.Hasler, J. & Marr, H. B. Finding a roadmap to achieve large neuromorphic hardware systems. Front. Neurosci. 7, 118 (2013).

115.Hasler, P. E., Diorio, C., Minch, B. A. & Mead, C. Single transistor learning synapses. In Advances in Neural Information Processing Systems Vol. 7 (eds Tesauro, G., Touretzky, D. S. & Leen, T. K.) 817–824 (Neural Information Processing Systems Foundation, 1995). This was one of the first works to use a non-volatile memory device—specifically, a floating-gate transistor—as a synaptic element.

116.Holler, M., Tam, S., tro, H. & Benson, R. An electrically trainable artificial neural network (ETANN) with 10240 ‘floating gate’ synapses. In Int. Joint Conf. on Neural Networks Vol. 2, 191–196 (1989).

117.Chen, P.-Y. et al. Technology–design co-optimization of resistive cross-point array for accelerating learning algorithms on chip. In Proc. Eur. Conf. on Design, Automation & Testing 854–859 (IEEE, 2015).

118.Chakraborty, I., Roy, D. & Roy, K. Technology aware training in memristive neuromorphic systems for nonideal synaptic crossbars. IEEE Trans. Em. Top. Comput. Intell. 2, 335–344 (2018).

119.Alibart, F., Gao, L., Hoskins, B. D. & Strukov, D. B. High precision tuning of state for memristive devices by adaptable variation-tolerant algorithm. Nanotechnology 23, 075201 (2012).

120.Dong, Q. et al. A 4 + 2T SRAM for searching and in-memory computing with 0.3-V V DDmin. IEEE J. Solid-State Circuits 53, 1006–1015 (2018).

121.Agrawal, A., Jaiswal, A., Lee, C. & Roy, K. X-SRAM: enabling in-memory Boolean computations in CMOS static random-access memories. IEEE Trans. Circuits Syst. I 65, 4219–4232 (2018).

122.Eckert, C. et al. Neural cache: bit-serial in-cache acceleration of deep neural networks. In Proc. 45th Ann. Int. Symp. Computer Architecture 383–396 (IEEE, 2018).

123.Gonugondla, S. K., Kang, M. & Shanbhag, N. R. A variation-tolerant in-memory machine-learning classifier via on-chip training. IEEE J. Solid-State Circuits 53, 3163–3173 (2018).

124.Biswas, A. & Chandrakasan, A. P. Conv-RAM: an energy-efficient SRAM with embedded convolution computation for low-power CNN-based machine learning applications. In Int. Solid-State Circuits Conf. 488–490 (IEEE, 2018).

125.Kang, M., Keel, M.-S., Shanbhag, N. R., Eilert, S. & Curewitz, K. An energy-efficient VLSI architecture for pattern recognition via deep embedding of computation in SRAM. In Int. Conf. on Acoustics, Speech and Signal Processing 8326–8330 (IEEE, 2014).

126.Seshadri, V. et al. RowClone: fast and energy-efficient in-DRAM bulk data copy and initialization. In Proc. 46th Ann. IEEE/ACM Int. Symp. Microarchitecture 185–197 (ACM, 2013).

127.Prezioso, M. et al. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 521, 61–64 (2015).

128.Sebastian, A. et al. Temporal correlation detection using computational phase-change memory. Nat. Commun. 8, 1115 (2017).

129.Jain, S., Ranjan, A., Roy, K. & Raghunathan, A. Computing in memory with spin-transfer torque magnetic RAM. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 26, 470–483 (2018).

130.Jabri, M. & Flower, B. Weight perturbation: an optimal architecture and learning technique for analog VLSI feedforward and recurrent multilayer networks. IEEE Trans. Neural Netw. 3, 154–157 (1992).

131.Diorio, C., Hasler, P., Minch, B. A. & Mead, C. A. A floating-gate MOS learning array with locally computed weight updates. IEEE Trans. Electron Dev. 44, 2281–2289 (1997).

132.Bayat, F. M., Prezioso, M., Chakrabarti, B., Kataeva, I. & Strukov, D. Memristor-based perceptron classifier: increasing complexity and coping with imperfect hardware. In Proc. 36th Int. Conf. on Computer-Aided Design 549–554 (IEEE, 2017).

133.Guo, X. et al. Fast, energy-efficient, robust, and reproducible mixed-signal neuromorphic classifier based on embedded NOR flash memory technology. In Int. Electron Devices Meeting 6.5 (IEEE, 2017).

134.Liu, C., Hu, M., Strachan, J. P. & Li, H. Rescuing memristor-based neuromorphic design with high defects. In Proc. 54th ACM/EDAC/IEEE Design Automation Conf. 76.6 (IEEE, 2017).

135.Tuma, T., Pantazi, A., Le Gallo, M., Sebastian, A. & Eleftheriou, E. Stochastic phase-change neurons. Nat. Nanotechnol. 11, 693–699 (2016).

136.Fukushima, A. et al. Spin dice: a scalable truly random number generator based on spintronics. Appl. Phys. Express 7, 083001 (2014).

137.Le Gallo, M. et al. Mixed-precision in-memory computing. Nature Electron. 1, 246 (2018).

138.Krstic, M., Grass, E., Gürkaynak, F. K. & Vivet, P. Globally asynchronous, locally synchronous circuits: overview and outlook. IEEE Des. Test Comput. 24, 430–441 (2007).

139.Choi, H. et al. An electrically modifiable synapse array of resistive switching memory. Nanotechnology 20, 345201 (2009).

140.Serrano-Gotarredona, T., Masquelier, T., Prodromakis, T., Indiveri, G. & Linares-Barranco, B. STDP and STDP variations with memristors for spiking neuromorphic learning systems. Front. Neurosci. 7, 2 (2013).

141.Kuzum, D., Jeyasingh, R. G., Lee, B. & Wong, H.-S. P. Nanoelectronic programmable synapses based on phase change materials for brain-inspired computing. Nano Lett. 12, 2179–2186 (2012).

142.Krzysteczko, P., Münchenberger, J., Schäfers, M., Reiss, G. & Thomas, A. The memristive magnetic tunnel junction as a nanoscopic synapse–neuron system. Adv. Mater. 24, 762–766 (2012).

143.Vincent, A. F. et al. Spin-transfer torque magnetic memory as a stochastic memristive synapse for neuromorphic systems. IEEE Trans. Biomed. Circuits Syst. 9, 166–174 (2015).

144.Sengupta, A. & Roy, K. Encoding neural and synaptic functionalities in electron spin: a pathway to efficient neuromorphic computing. Appl. Phys. Rev. 4, 041105 (2017).

145.Borghetti, J. et al. ‘Memristive’ switches enable ‘stateful’ logic operations via material implication. Nature 464, 873–876 (2010).

146.Hu, M. et al. Dot-product engine for neuromorphic computing: programming 1T1M crossbar to accelerate matrix-vector multiplication. InProc. 53rd ACM/EDAC/IEEE Annual Design Automation Conf.21.1 (IEEE, 2016).

147.Sheridan, P. M. et al. Sparse coding with memristor networks. Nat. Nanotechnol. 12, 784–789 (2017).

148.Wright, C. D., Liu, Y., Kohary, K. I., Aziz, M. M. & Hicken, R. J. Arithmetic and biologically-inspired computing using phase-change materials. Adv. Mater. 23, 3408–3413 (2011).

149.Le Gallo, M., Sebastian, A., Cherubini, G., Giefers, H. & Eleftheriou, E. Compressed sensing recovery using computational memory. In Int. Electron Devices Meeting 28.3.1 (IEEE, 2017).

150.Rosenblatt, F. The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65 386 (1958).

151.Bi, G. Q. & Poo, M. M. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472 (1998).

翻译：张田、Leo

审校：胡鹏博、郭瑞东

编辑：张希妍

原文地址：https://www.nature.com/articles/s41586-019-1677-2

话题：