为什么经济必须持续增长？多主体模型揭示规模、复杂性与财富增长的关联-集智俱乐部的财新博客-财新网

导语

现代经济已经从简单的人类互动演变为非常复杂的系统。经济行为人可以付出一定代价，利用经济体的自由度对其进行监管、篡改或干预，使得财富流向对他们有利的方向。当干预变得普遍，不同行为人的微观经济策略可以引发短期宏观经济效应。一个“被操纵”的经济体会带来怎样的效应？日益增长的经济复杂性和财富规模有何影响?在2021年9月发表于Physical Review X 的一项研究中，西班牙国家生物技术中心的Luís Seoane通过建立博弈模型来研究“被操纵”经济体及其动力学。

研究领域：基于主体的建模，经济复杂性，少数者博弈，多数者博弈

Sitabhra Sinha | 作者

胡一冰 | 译者

刘培源 | 审校

邓一雪 | 编辑

1. 研究背景：被操纵的经济

“经济被操纵了！”这一说法由Bernie Sanders和Donald Trump在2016年美国总统竞选期间提出，这可能是政治立场相反的两人拥有的唯一共同观念。但“被操纵”对经济体及其演化意味着什么？为了解决这个问题，西班牙国家生物技术中心的Luís Seoane将经济行为人（Economic actors）建模为博弈过程中的个体来进行探索[1]，该研究已于近日发表在 Physical Review X 上。

论文题目：

Games in rigged economies

论文地址：

https://journals.aps.org/prx/abstract/10.1103/PhysRevX.11.031058

研究表明，随着复杂性和规模的增加，受操纵的经济体会经历一系列转型，并伴随“卡特尔”的形成和解散。如果一个经济体的规模跟不上其日益增长的复杂性，财富分配模式将会出现大幅波动，不平等现象急剧上升，甚至导致经济崩溃。

图1. 卡特尔（cartel）即垄断利益集团，是生产同类商品的企业为了垄断市场、获取高额利润而达成有关划分销售市场、规定产品产量、确定商品价格等方面的协议所形成的垄断性企业联合。

使用博弈论（game theory）来研究经济现象可以追溯到冯·诺伊曼（John von Neumann）在上世纪中期的工作[2]。此后，博弈论很快成为经济学家的通用语言（lingua franca），随后也发展成为物理界的一个研究领域。例如，统计物理学家已经研究了不同版本的“少数者博弈”（minority game）——少量个体在两个可能性中做出选择，被最少个体青睐的选项为获胜选择，这可以用来探索简单的自适应系统中的涌现性[3]。

少数者博弈可以用来模拟个体因为稀缺资源而竞争的情形，包括金融市场。然而，经济中也存在大多数人占优势的情况。例如，某个特定选项被予以正反馈，如加入抵制行列[4]。Seoane指出，被操纵的经济体兼具少数者博弈和多数者博弈（majority games）的特点[5,6]。

2. 建模思路：经济干预下的多方博弈

在Seoane的模型中，首先假设多个个体同时参与多个博弈。每次博弈都需要从两个备选项中选择一种。个体也可以通过付费的经济干预形式来操纵博弈过程以支持自己的决策。在每一轮中最优决策是大多数支付费用的个体所选择的行动。

每一轮由若干次博弈组成，增加每一轮的博弈次数可以增加经济中的自由度，从而丰富其复杂性。每一次博弈结束后，获胜个体将平分指定数额的奖金。奖金的价值与博弈次数之积是每一轮博弈中个体之间重新分配的“总财富”。因此，这个“总财富”可以衡量经济规模，是和复杂性一样重要的模型参数。

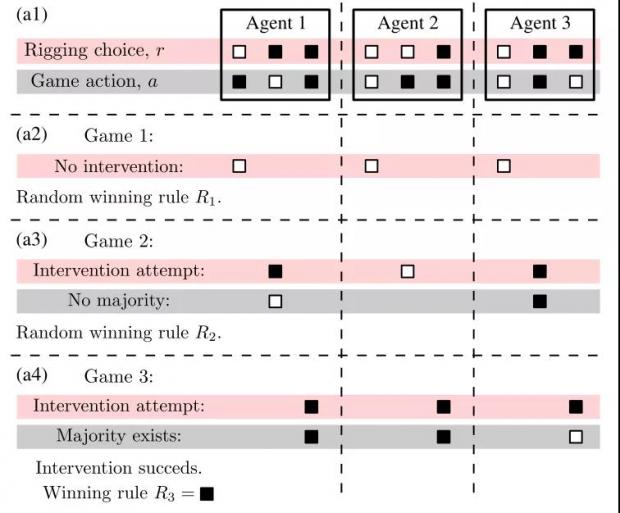
图2. “被操纵”经济体的博弈过程示意图

图2为Seoane在研究中所提出的博弈模型示意图。子图（a1）表示有三个个体参与经济博弈，粉色一行r代表各自是否采取经济干预（黑色方形代表采取，白色代表未采取），灰色一行a代表个体的决策行为（分别有黑白两种独立选项）。图中每个个体都会进行三次博弈，每次的行为均表示在子图（a1）的黑色框内。子图（a2-a4）反映每一次博弈最优策略的产生。

在第一次博弈中，三个个体均未采取经济干预手段，那么最优策略会在黑白两种策略中随机诞生。在第二次博弈中，个体1、3采取经济干预，但由于二者选择恰好相反，最优策略会在个体1、3二人的选择中随机产生。在第三次博弈中，所有个体都采取经济干预，个体1、2选择黑色策略后形成了多数者优势，则本次博弈的最优策略为黑色。

为了观察个体最优策略随着经济发展如何变化，Seoane在模型中加入了进化过程：个体可以在每一轮博弈结束后复制之前的行为，之后每个子代都有很高的概率采用与其亲代相同的策略。由于复制成本是固定的，更多收益的个体会复制出更多的参与者。

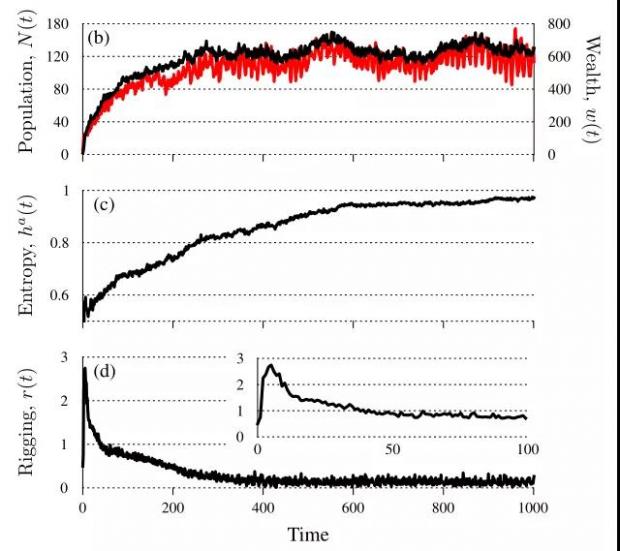
图3.“被操纵”经济体及其演化

图3反映基于特定参数值的“被操纵”经济体随时间的演化模拟结果。子图（b）的纵轴 N(t) 为参与博弈的个体数，当一个个体的财富高于某个特定阈值，将会产生子代参与者，系统博弈个体数增加；相反，当某个体的财富值小于0，则将被移出系统。子图（c）中的熵 ha(t) 反映参与者决策的异质性程度，ha(t)=0，代表所有个体做出相同决策。子图（d）中的 r(t) 表示系统内所有的经济干预压力，即共有多少个体同时采取经济干预。

3. 研究结论：个体之间关系的演变

Seoane注意到，在复杂度固定的情况下，小型经济体中会产生具有不同策略的个体，并且获胜者通常倾向于少数派。随着经济规模的扩大，个体可以获得更多财富来繁衍后代，并支付操纵博弈所需的干预成本。于是，个体从少数者博弈转向多数者博弈，这意味着经济增长导致个体之间关系向协作过渡，即卡特尔形成，策略多样性随之下降。

反之，如果复杂性（每轮博弈次数）的增长速度快于经济的增长速度，每次博弈的相对收益将会减少，个体会在多次博弈中寻找被少数人青睐的选项。这一转变又将导致卡特尔的解体，个体可采用的策略也更多样化。

Seoane还研究了经济体在其他规模-复杂性关系下的运行情况。例如，当每次博弈中的经济干预总额恒定，经济规模就会随着博弈次数的增加而呈线性增长。在这个关键的“复杂性阈值”上，个体数量规模的分布从单峰型向双峰型转变，如图4子图（e）所示。这一转变引起个体数量的极大波动，甚至能威胁到经济的稳定。该转变也能通过个体财富的分布体现出来，在大幅波动的情况下财富分布的尺度变宽，即个体间的不平等现象加剧，如图4子图（g）所示。

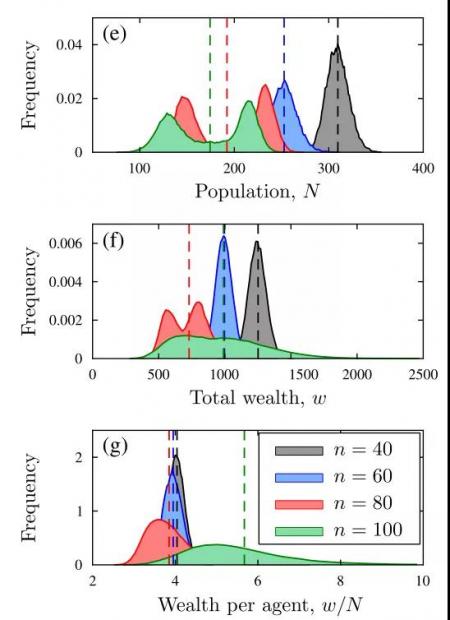
图4.个体规模N、总财富ω和人均财富值ω/N的分布情况。

4. 研究启示：垄断与反垄断

Seoane观察到的一些结果来自于他在建模时做出的特定选择。例如，经济规模增长时，向个体协作行为的过渡可能是由于假设干预成本一成不变。在现实中，干预成本与经济规模有关，并会因参与者而异。这个模型的另一个瑕疵是假设所有的个体都有能力操纵游戏，这忽略了现实经济中富人与穷人不对称的经济影响力。

即使有这些不足，Seoane的模型仍具有重要意义。它为后来研究者提供了一个探索现实世界中受操纵的经济体的框架，比如在某些经济体中个体接收信息能力各有不同。

例如，修改模型参数或许可以反映出，信息弱势个体如何利用协作的产生来获取优势，就像其他基于个体的模型[8]所发现的那样。中世纪商业行会的历史表明，实力较弱的玩家会对系统进行这样的反操纵，这些机构通过联合禁运来抵制强大的地方统治者的肆意征用，证明了一个被操纵的经济环境并不一定意味着小人物没有机会对抗强者。

参考文献

[1]L. F. Seoane, “Games in rigged economies,” Phys. Rev. X 11, 031058 (2021).

[2]J. von Neumann and O. Morgenstern, Theory of games and economic behavior (Princeton University Press, Princeton, 1944)[Amazon][WorldCat].

[3]D. Challet et al., Minority games: Interacting agents in financial markets (Oxford University Press, New York, 2005)[Amazon][WorldCat].

[4]T. C. Schelling, Micromotives and macrobehavior (W. W. Norton, New York, 1978)[Amazon][WorldCat].

[5]J. Vitting Andersen and D. Sornette, “The $-game,” Eur. Phys. J. B 31, 141 (2003).

[6]Y. Baek et al., “Market behavior and performance of different strategy evaluation schemes,” Phys. Rev. E 82, 026109 (2010).

[7]J. E. Stiglitz, “The American economy is rigged,” Sci. Am. 319, 56 (2018).

[8]V. Sasidevan et al., “When big data fails: Adaptive agents using coarse-grained information have competitive advantage,” Phys. Rev. E 98, 020301 (2018).

[9]A. Greif et al., “Coordination, commitment, and enforcement: The case of the merchant guild,” J. Polit. Econ. 102, 745 (1994).

原文：https://physics.aps.org/articles/v14/129

话题：