从细胞到国家—共同的异速生长法则

jake 集智俱乐部

本期主推复杂系统中的临界现象，其中异速生长是普遍存在于各类复杂系统的临界现象的重要表现

引言

  近年来，随着所谓的“大数据”时代来临，复杂系统科学研究的基本方法论正在发生着天翻地覆的变化。从早期的纯哲学思辨，再到后来的计算机模拟，复杂系统研究终于开始采用“物理学范式”：从实证数据中来，得到一般性理论，再到具体的预测和实验中去。

    物理学范式的一个成功的应用案例就是万有引力的研究（记得王雄曾经做过一次关于引力理论的讲座）。的确，从第谷、伽利略再到牛顿与爱因斯坦，物理学家花费了将近300年的时间，终于将行星运动的观测数据与完美的数学理论（爱因斯坦广义相对论）联系了起来。这就是物理学的范式，一步一步地，虽然举步维艰，但是终于达到了可以精确预测星体运行的物理学。

   在复杂系统研究领域，随着人们更加自觉地开始利用大量的数据，一些类似伽利略行星三大定律的定量规律已经慢慢地浮现出来。而其中最显眼的一条普适规律就是我们今天要讲的异速生长律了。所谓的异速生长律，就是指系统的两个宏观变量X和Y之间服从一个幂律方程：

Y=cX^a 

其中c和a都是常数。这个方程有其深刻的内涵，目前已被证实适用于从细胞到国家横跨将近三十个数量级的复杂系统。

一、生物学中的异速生长律

1、异速生长(allometry)一词的来源

   下面，我们来详细介绍异速生长律现象。异速生长律这个词最早是由生物学家Huxley 和Tessier 在1936年提出的。他们通过研究招潮蟹（fiddler crab，一种螃蟹）的钳子大小随着螃蟹身体而变化，发现了两者之间的幂律依赖关系，如下图所示：

（图1. 该图摘自：http://www.nature.com/scitable/knowledge/library/allometry-the-study-of-biological-scaling-13228439）

   随着招潮蟹从小长到大，它的身体在某个时刻t的尺寸（用螃蟹壳的宽度来衡量）是X(t)，而它的钳子的大小（如上图左图红色线段所示）用Y(t)来表示，则这两个变量之间服从下面的方程：

Y(t)=cX(t)^^a

在这里c,a都是常数。如果对上面等式两边取对数，则得到：

ln(Y(t))=log(c)+a log(X(t))

我们发现，ln(Y(t))和log(X(t))构成了一个对线性依赖的变量。通过将实际测量的螃蟹尺寸数据画在双对数坐标轴上，并且用最小二乘法可以从实际数据估计出参数c和a（如上图右图所示）。结果他们发现，实际估计出来的参数a大于1（大概为1.57，为了对比，斜率为1的直线在上面右图所示），这就意味着如果招潮蟹体积增大了2倍，它的钳子的体积增长倍数要大于2倍，因此钳子的增长速度要远快于它的体积增长速度，这就是异速生长（Allometry或者Allometric scaling）一词的来源。（参考Nature上面的Allometry: The Study of Biological Scaling一文）

   Allometry是一个合成词，allo-表示相异的，而-metry这个后缀则有测量、度量的意思。因此，这两个词根合起来就是相异的两种测量。而这里的相异又是何含义呢？我们要先理解Allometry的反义词Isometry一词，这里Iso是表示相同的。在上面的例子中，如果螃蟹钳子的生长速度和它的身体的生长速度是相同的，也就是说幂律指数a=1，那就表示钳子和它的体积是线性的，它们以相同的速度增长（Isometry）。但是，事实上，我们测量到的真实数据告诉我们，这两个变量的生长速度并不一致，钳子快，身体慢，它们两者不协调，因此，就称为异速生长。

   根据Wikipedia上面的解释，这里所说的同速增长Isometry并不一定就等于是线性增长关系，而是一种正常的按照欧几里德几何的增长方式。因此，Isometry就成为了一种作为参考和比较的类似于统计上的零模型的东西（Null model）。

   比如说，对于欧几里德几何体来说，一个物体的面积的增长与该物体体积的增长呈现出2/3的幂律关系，即面积正比于体积的2/3次幂。让我们考虑生物体，例如人类大腿的截面面积，假如随着人体积的增长，界面面积呈现了2/3幂次的增长，那么该截面面积就是同速生长（相比较欧几里德几何体来说）。但是如果增长速度不等于2/3，那么我们就说大腿截面面积的增长属于异速生长。

2、各种异速律

   在上面的例子中，我们是将同一个生物个体不同时刻的钳子大小和个体大小两个变量作为数据点画在双对数坐标下得到异速生长律，这种异速生长律被称之为个体发生异速律（ontogenetic allometry ）。我们也可以这样做：在同一个时间，找来一堆招潮蟹，这堆招潮蟹有大有小，我们将它们的钳子大小作为一个变量Yi(i表示个体），个头大小作为另一个变量Xi，然后将这些数据点画在同一个坐标轴上。这个时候，我们仍然可能得到一个Yi与Xi之间的幂律关系，但是这个幂律关系描述的是不同个体在同一个时刻的异速生长律。在生物学中，这被称为静态的异速律(Static  allometry)。

   另外，除了研究同一个物种不同的个体在同一个时间截面内的异速律，我们还可以研究不同的物种在同一个时间截面内平均值的异速生长律。前者称为种内的异速生长律（intraspecific allometry），后者称为种间的异速生长律（interspecific  allometry）。

   例如，我们考虑生物体的新陈代谢F和它们的重量M之间的异速生长关系。Max  Rubner曾经对狗这个物种研究过这两个变量之间的关系，由于狗的品种繁多，而且他们的重量M的变化范围很大，因此画在双对数坐标下，会有一个很宽广的范围，可以研究种内的异速生长律。他的数据指出，狗种内的异速生长律的幂指数是2/3左右。后来又有人用鸟来做种内的异速生长律，结果也接近2/3。

   然而，Kleiber（1932）发现，如果我们研究种间的F与M之间的关系。即找来不同的物种，并测量每个物种多个个体的平均新陈代谢量以及生物体重量，然后将这些数据点画在同一张图上，就会得到幂指数为3/4的异速生长律。因此，我们看到尽管是同一对变量，种间和种内的异速生长律幂指数也是很不同的。

3、3/4幂律—生物中的“开普勒”定律

   尽管当前生物学已经积累了超海量数据，定量化研究也是势在必行。但是笔者认为，在众多的定量规律之中，Kleiber预言的生物体的新陈代谢和生物量之间的3/4幂律是最重要的一个，也是最接近天体中的开普勒定律的候选者。

   因为Kleiber的3/4定律不仅仅给出了所有不同物种的统一的幂律关系，还指出这些幂律关系具有完全同样的幂指数3/4，更让人吃惊的是，这个定律的适用范围非常广泛，小到分子、细胞器、细胞，大到鲸鱼、大象，新陈代谢与生物量之间的3/4次幂律始终成立。大自然再一次在看似纷乱复杂的生物世界中展示了它的统一的数学之美。

    继Kleiber等在早期针对哺乳动物得到了3/4幂律之后，Geoffery West等人又将这一定律的适用范围进一步扩大到了微观生物世界。在2002年的PNAS刊物上的一篇文章《Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals》中，他们指出从完整的生物体，到细胞、线粒体甚至到色素细胞氧化酶分子，在这横跨了27个数量级的上，所有这些生命现象都遵从同一个指数的3/4幂律。如下图所示：

本图摘自：

Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals

   值得注意的是，对于不同尺度的生物系统来说，虽然他们的幂指数都非常接近3/4，但是这些直线的截距（也就是log(c)却不尽相同)。这意味着：处于同一条直线上的生物体具有相类似的网络结构（它们是同一种系统经过尺度变化，不断扩大出来的，这类似于一个个体从小到大的诚征）。而处在不同直线段上的生物体却不一定具有相似的结构。有关Kleiber定律以及其它的种间的异速生长律的详细介绍，请大家参看：《流的探索》。

   总而言之，我们可以将各种异速律进行如下的分类：

1、个体发生异速律（ontogenetic allometry ）

2、静态异速律（Static allometry）

    2.1 种内异速律（Intraspecific allometry）

    2.2 种间异速律（Interspecific allometry）

三、从城市到国家

1、城市—创新的来源

   异速生长现象如果说仅适用于生物系统，那么它还不够普适。但事实上，近期越来越多的研究表明，异速生长方程：Y=cX^a 是一个相当普遍的方程，只不过在其他系统中，我们一般找不到统一的幂指数a。

   例如，当我们研究人类城市的时候，就会发现很多变量都随着城市规模（人口数）的增长而呈现异速生长方程。而这些变量所对应的幂指数大小不一。例如，在Luis Bettencourt等人的文章《Growth, innovation, scaling, and the pace of life in cities》中，作者研究了多种变量与城市人口之间的静态异速生长关系（同一个时间截面，不同的城市）：

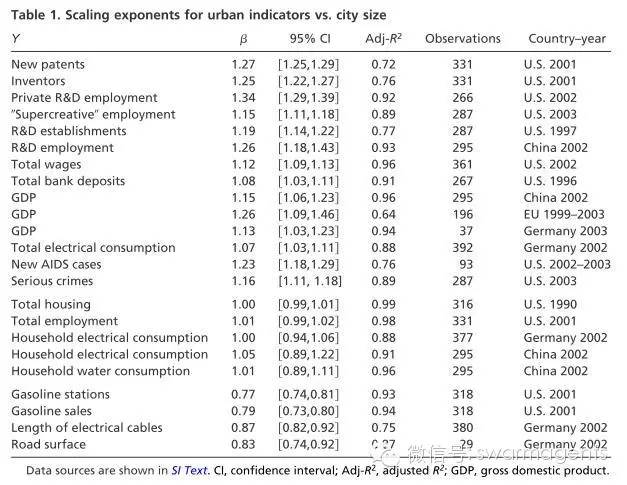
   如上表所示，最左边一列是城市的各种指标（即变量Y），例如一个城市在一年内新申请的专利数量、城市的总产值（GDP）、总的房屋数目、总电量消耗、加油站数目等等。第二列则给出了异速生长方程Y=cX^a中的幂律指数。第三列是拟合优度R²、第四列是在幂律方程中拟合点的数目，最后一列则指出了不同的数据来源，它们来自美国、中国、德国、欧洲的不同时期。

   我们看到，这些变量的幂指数大小虽然都不一样，但是基本都可以分成三大类：>1,<1和约等于1。这三大类变量依次被称为超线性增长、亚线性增长和线性增长。幂律指数a的大小反映出了该变量随着城市的增长所体现出来的规模效应。

  从幂律方程Y=cX^a中变形，我们可以得到：

                                         Y/X=cX^(a-1)

  在这里，方程的左边是人均拥有的Y变量（例如人均GDP，人均加油站数量等等）。如果a>1，那么方程右侧的幂指数就大于0，也就是人均拥有的Y变量会随着城市的增长而增大。如果a<1，则体现为人均Y会随着城市的增长而减小。如果a约等于1，就意味着人均Y不随城市规模而变化。

  这又意味着什么呢？让我们用GDP作为Y来说明该方程的意义。我们知道GDP衡量的是一个经济单位在一段时期内创造的总产值。那么Y/X就表示一个城市的人均GDP。通过实证研究我们得到不同国家的城市的幂律指数都>1（在上表中基本上是1.2左右），也就意味着人均GDP会随着城市规模的增长而增长。

  在中国，每年都会有大量的人口涌进像北京、上海这样的大城市，在全世界，超过一半的人口是居住在城市的，而且这种比例还在增大。为什么会出现这种情况？人们为何希望聚集到大城市呢？通过方程Y/X=cX^0.2我们不难看到，这是因为城市越大，人均产出（或者等价地即为人均收入）会随着城市规模的增大而增加。所以，城市越大就意味着平均来说每个人的收入就会增加（暂时忽略贫富之间的差距），所以很多人更愿意居住在大城市。

   让我们再来看一个变量Y为石油销售量。在表中，这个变量的幂指数a<1，这意味着随着城市的增大，人均所消耗的石油在减少。因此，人们聚集在一起形成大城市实际上是一种更加经济地使用石油资源的方式。

   总而言之，根据该表格，很多与创新、财富增长有关的变量都具有超线性关系，而与能量、资源消耗有关的变量都呈现出亚线性关系，这些都说明了城市是一种具备规模经济效应的有机体。当然，城市规模的增加也有负面效应，例如，人均犯罪数量、人均艾滋病感染数量也都会随着城市规模的增加而增加。

2、国家的异速生长

   以上，我们介绍了生物以及城市中的异速生长现象。但是这些都是别人的研究。下面，我就来讲讲我自己做的研究。即在更大的国家尺度上来探索异速生长律。以下讨论主要基于我们已发表的一篇论文： J. Zhang, T. Yu: Allometric scaling of countries, Physica A 389 (2010) 4887–4896。

   我在2007年左右写作《流的探索》系列文章的时候就开始对异速生长定律这块非常感兴趣。但是经历了3年多的时间，才发表了第一篇这方面的论文。原因就是，要做这种研究，最重要的是找到实证数据。而对于以前从没有接触过数据的我来说，这件事情还真的形成了一道门槛。不过，幸运地是，我意外地发现，原来我安装的Mathematica 6.0软件之中就包含了大量的数据。其中，Mathamtica中有一个命令叫做CountryData。利用它，你可以利用自己的PC机连接到一个Wolfram公司提供的庞大的在线数据库，从而访问世界各国各方面的数据（包括地理、人口、经济、贸易等）。有了这个大的数据库，我就可以展开大量的关于异速生长律的研究。

   在这个研究中，我们对273个国家或地区的104个数值型的变量进行了系统性的静态异速生长律研究。首先，我们将所有这些变量划分成了两类：1、广延型的变量；2、强度型变量。在物理中，所谓的广延型变量是诸如能量、质量、熵等具有子系统可加性的变量。在国家中，一些宏观总量，如人口、GDP、面积、出口、进口等都属于广延型变量。而平均的人均GDP，人口的生育率、死亡率等类似于物理中的温度、压强被称为强度量。

   对于广延性的变量，我们分别研究了它们和三种不同的国家尺度变量（分别是地理尺度，即国土面积、人口尺度，即总人口和经济尺度即GDP）做异速生长律分析，即探索Y=cX^a是否成立，这里X是面积、人口和GDP这三种不同的尺度。Y是各种广延性变量。

  我们得到了一些有趣的结论如下：

  1、国家作为更大的经济体与城市呈现出明显的差异

  例如，如果我们仍然研究人口和GDP这两个变量的异速生长关系，就会发现虽然Y=cX^a这个方程仍然成立，但是幂指数a会非常接近于1，而不是大于1，也就是说，对于国家来说，GDP和人口近似呈现出线性的关系。如下图：

   在这张图中，每个数据点都表示一个国家。红色的直线和黑色的虚线分别是用普通最小二乘法和主轴回归法得到的对异速生长关系幂指数的估计值。在本研究中，我们一般采纳主轴法得到的结果（关于不同回归方法的介绍，我会另外写文章）。因此，国家的人口与GDP之间的关系呈现线性。

   也许你会认为这个数据并不好，噪声很大，因此统计的显著性并不高（R²=0.59），这样得到的幂指数a的估计会不会不准呢？事实上，我们可以通过选择不同的属性来得到更加准确、显著性更高的人口与产出之间的关系，如下图：

  我们通过把横轴的人口属性用就业的劳动力总数来替代，纵轴用等价购买力重新核算的GDP来代替普通的GDP，我们就会得到统计显著性更高的异速生长关系（事实上R^2从0.59提高到了0.88），而幂指数始终在1附近，几乎没变。我们知道由于世界上不同国家的差异非常大，因此用等价购买力折算的GDP比直接用GDP会更能反映出国家的实际产出能力。而在人口方面，由于并不是所有的人口都处于就业而产生产出的状态，因此利用就业的劳动力会去除更多的噪音。由此，我们可以确定，对于国家来说，GDP与人口成正比。

  由此，我们已经得到了一个与城市截然不同的结论。我们知道在城市中，人口与GDP的关系是超线性的，即随着城市规模的增大，人均产出会增加。但是对于国家来说，人口越多的国家并不意味着更富裕，即越高的人均GDP（想一想印度和中国这两个国家，在图中的最右侧的两个点，就可以知道了）。事实上，我们与Bettencourt的城市文章进行了对比发现了更多的不同：

  从这张表，我们可以清楚地知道，随着人口的上升，城市的人均使用面积会减少，人均产出、电力消耗、感染艾滋病的总数会提高，石油消耗会减少，这体现了城市的规模效应。对于国家来说，随着人口的增加，人均用地、电力消耗、石油消耗、艾滋病感染都会增加，而人均产出近似不变，这说明，相比较城市来说，国家这种更大规模的系统并不呈现出规模经济效应。

  为什么会存在这样的不同呢？很有可能国家相对于城市来说，他的封闭性越差，人口、物品、能量的流入和流出会受到更大的限制。这导致了国家不能形成有效的自组织系统。另外，由于城市属于人口密集的地区，而国家中大片的土地是处于没有人口居住的农村地区，所以国家的总产出近似与人口成正比而并非呈现出超线性关系。

3、GDP会比人口更好地衡量国家的尺度

  我们发现，很多宏观变量都与国家的GDP而非人口形成了显著性很高的幂律关系，如下表所示：

  我们看到，从石油消耗、电力消耗到出口总额、进口总额，再到电话线长度、收音机电台个数、互联网用户数、公路总长度都可以用国家的GDP得到预测。而且，统计的显著性R²都高于0.6。

   有几个幂律关系非常有趣，例如进口总额、出口总额与GDP的关系。如果把国家看作是由货币流构成的宏观系统，那么进口总额、出口总额类似于国家经济体的新陈代谢，而GDP相当于经济体的生物体的存量。因此，出口、入口与GDP的异速生长律可以看作是经济流的Kleiber律。

   另外一个有趣的幂律关系是碳排放（Carbon Emission）与GDP之间的超线性关系。现在一个时髦的词就是低碳经济，人们正在想尽一切办法减少碳排放。但是，根据我们的研究，碳排放是与GDP呈现显著性很高的超线性关系的，因此GDP越高，碳排放就会越高。这是一种系统性的规律，很难通过个体行为而改变。因此，要抑制更多的碳排放，恐怕唯一的办法就是减少人类的产出。

    最后，我们还研究了各种强度量与人均GDP之间的关系。如下图展示的两个例子：

   随着国家变得越来越富有（人均GDP的提高），总和生育率下降而平均年龄生高。而且这些强度量与人均GDP呈现了幂律的关系。我们猜想这类幂律关系与人类作为生物体需要进行新陈代谢，因此必然遵循代谢生态学的约束（参看《流的探索》）。

 四、标度律现象

   关于异速生长律，我们已经说了很多。但是，熟悉复杂系统研究的朋友可能还知道，除了异速生长以外，近年来，人们还发现了普遍的标度律现象(Scaling)。所谓的标度现象就是大家俗称的幂律现象，只不过我更喜欢Scaling这个词，因为它实际上包含了一种系统随着尺度发生变化而变化的特性，它比直白而肤浅的幂律一次有更深的刻画。例如复杂网络中节点度的无标度分布（Scale-free），例如语言中的Zipf律，再如经济中的Pareto分布，还有生物学中的异速生长标度律现象。

  总结来看，从细胞到国家，无论是生物系统、生态系统还是人类经济社会系统都遵从相同的幂律方程：

  Y=cX^a

  这就是异速生长律，它是一种横贯了不同复杂系统的精确而定量的数学方程。在这篇文章中，我们展示了各种各样的实证数据复合这个方程。但是，究竟为什么会有这个方程？他的机制是什么？如果我们把异速生长律比喻成引力中的开普勒定律，那么我们呼唤复杂系统中的牛顿出现(需要解释开普勒定律的万有引力定律与牛顿三定律)。复杂系统的牛顿力学会是什么样子的呢？ (或者说复杂系统的“微积分”，复杂系统的“大统一理论”)

参考文献

 

1. ↑ [1],Nature文章：Allometry: the study of bioloical scaling

2. ↑ West, Geoffery; William H. Woodruff, James H. Brown (2002). "Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals". PNAS 99: 2473-2478.http://www.pnas.org/content/99/suppl.1/2473.full.

3. ↑ ^{3.0 3.1} Luís, M. A. Bettencourt*; José Lobo,Dirk Helbing,Christian Kühnert,Geoffrey B. West (2007). "Growth, innovation, scaling, and the pace of life in cities". PNAS 104 (17): 7301-7306.http://www.pnas.org/content/104/17/7301.abstract.

4. ↑ Zhang, Jiang; Tongkui Yu. "Allometric scaling of countries". Physica A: 4887–4896. http://www.sciencedirect.com/science/article/pii/S0378437110006072.

5. ↑ Stumpf1, Michael P. H.; Mason A. Porter. "Critical Truths About Power Law". Science: 665-666.

 

---

让苹果砸得更猛烈些吧！！！

扫描二维码，关注集智俱乐部，

让我们离科学探索更近一步。