摘要：

 

本文回顾了社会传染的经典模型之一阈值模型的相关内容，并且根据近年来在线服务产品采纳行为传播的实证研究讨论了阈值模型的局限性。在此基础上，介绍了一个新的模型，该模型在传统的阈值模型中引入两个新的机制，从而成功地解释了现实生活中社会传播的现象。

阈值模型的研究历史

 

社会传染现象在现实生活中随处可见。例如信息的传播，新产品、新技术或新药物的普及，恐慌情绪的蔓延，又或者是经济市场中泡沫的产生与破灭等等。这些看似风马牛不相及的现象之间，却有一些共同的性质：它们都是从少数个体的行为“变异”开始（这些个体由于各种原因，例如公共信息的影响等，采纳了与周围人群不一样的行为），然后通过人群之间的相互作用，达到该行为的大规模流行（转变为集体行为）。

 

这类社会现象在20世纪中期开始引起社会经济学家们的关注，直至今日仍然是一个研究热点。科学家们提出了各种不同的模型来解释这类传染现象，其中一个非常经典模型是“阈值模型”[1]。这一模型由Granovetter在上世纪70年代末提出。Granovetter假定个体做出某个决定的一部分原因取决于周围有多少个体作出了相同的决定[2]。这是因为在真实社会系统中，决策者往往缺乏全局信息，又或者他们对所掌握的信息处理能力有限，导致他们习惯于观察周围人的决策来决定自己的行为。另一方面，除了这种外部因素，诸如个体习惯、爱好、宗教信仰等内在因素也会影响个体的决策。为此Granovetter引入了一个 “阈值”的概念，他假定个体从一个行为状态转变到另一个行为状态时存在一定的阈值。这一阈值由个体的内在因素决定：对于不同背景的人来说，其值是不一样的。因此个体做决策是外在刺激与内在因素相互博弈的结果——当外在刺激的程度超过个体的阈值时，个体就从一个状态转变到另一个状态。

 

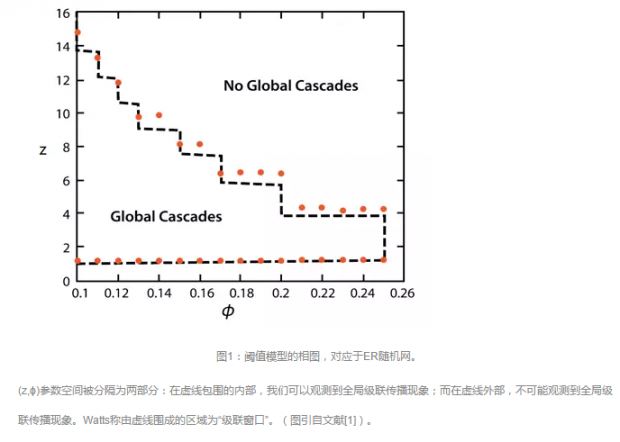
Watts最早彻底地研究了阈值模型的物理特性，并发展了一套优雅的方法来解析该模型[1]。他假定社会网络中的节点只有两种状态：0（非活跃态）或1（活跃态）。一个0态的节点会转变为1态，如果他的邻居节点中处在1态的人数比例超过了该节点的阈值，即 m/k≥ϕ ，其中k为个体的邻居节点数，m为邻居中处于1态的节点数目，ϕ为个体的阈值。在初始阶段，Watts假定所有节点都处于0态，除了一个随机选取的节点处于1态（微小扰动）。Watts发现，网络平均度 z 和个体平均阈值ϕ是影响整个动力学行为的两个重要的参数。如图1所示，在平均度z和阈值ϕ组成的参数空间中存在两个区域：在虚线包围的内部，我们可以观测到全局级联现象，也就是说绝大部分节点都能在极短时间内转变为1态；而在虚线外部，则不可能观测到全局级联现象，此时只有少数节点转变为1态（当总节点数趋于无穷时，所占比例趋于0）。我们还可以发现，当平均度从很小变到很大（固定ϕ），系统会经历两个不同的相变过程。其原因在于，当平均度很小时，网络是支离破碎的，因此任何初始扰动都无法大规模地传播；而当平均度很大时，阈值条件难以满足（此时需要更多处于1态的邻居数量），导致全局传播也不可能（同样当ϕ很大时也是如此）。一般来说，该级联窗口的下边界由网络的拓扑性质决定。例如对于ER随机网来说，网络中开始出现大的连接集团的相变点是在平均度z=1处，这与图1所展示的结果一致。而级联窗口的上边界则比较复杂，这实际上是由动力学过程决定的，但Watts同样巧妙地将其转换为一个静态可求解的渗流问题。

 

Watts将网络中的节点分为3类：

 

创新者，这类节点的阈值ϕ=0（由于外部影响自发转变为1态，在Watts模型中初始时刻只有一个创新者）。

 

脆弱的节点，这类节点的阈值满足0<ϕ≤1/k，即当邻居节点中有一个处于1态时，该节点就会转变为1态。

 

稳定的节点，即那些ϕ>1/k的节点。这样，能否引发全局级联传播的条件就等价于是否存在一个大的（跟系统大小相当）连通集团，这个集团全由脆弱的节点所组成。这是因为该集团中的任一节点转变为1态，都会继而引起集团中所有其他节点转变为1态（这些节点均满足ϕ≤1/k）。转换之后的静态结构问题可通过生成函数的方法进行解析求解，图1显示理论结果与数值模拟基本吻合（其中虚线是理论解析结果，点是模拟结果）。

 

阈值模型的新突破

 

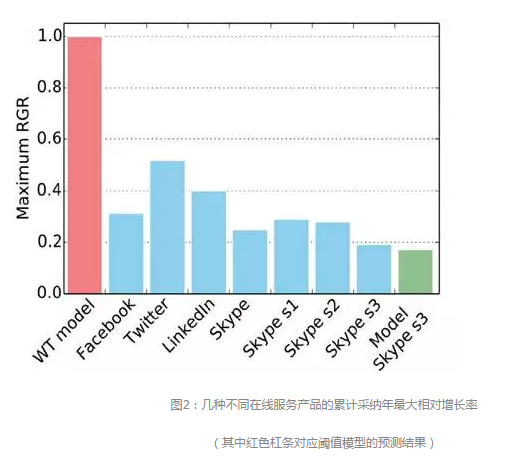
阈值模型尝试从微观角度（个体之间的相互作用）来解释集体行为涌现的原因。该模型中个体与其邻居之间有着一种社会加强作用（比如当个体发现周围有足够多的朋友采纳某种新产品时，他才有可能会采取同样的行为）。它不像生物系统中流行病的传播，在那里个体之间的相互作用是独立的，这意味着任意一个扰动都能引发全局的集体行为（例如初始时有一个个体行为变异，最终会引起网络中所有的节点都发生状态改变）。这显然与现实世界是相悖的。真实的复杂系统展现了一种Watts称之为“鲁棒而又脆弱”的特性：一个社会系统对于绝大多数的初始扰动（如新思想、新产品的出现等）都是稳定的（鲁棒性），但突然之间某些微小扰动可能会展现出巨大的、系统层面的宏观效应，即全局级联传播（脆弱性）。阈值模型能够成功解释这种现象，因此深受研究者们的青睐。然而随着近年来计算机科学及大数据领域的飞速发展，人们在一些在线实证数据中发现真实社会系统会表现出某些阈值模型无法解释的现象。例如除了快速的级联传播过程，社会系统有时候也可能会展现出极其缓慢的传播过程[4]。图2比较了几种常见的在线服务产品采纳行为的传播速度，其中纵坐标表示某一产品累计采纳的年最大相对增长率[4]。可以看出，与传统的阈值模型相比，真实的在线服务产品的采纳行为的传播速度要慢得多。

 

传统的阈值模型只关注能否发生全局级联传播的条件，而一旦发生级联效应，网络中的大部分节点便会在极短的时间内转变为1态。为了解释这种缓慢传播的现象，我们需要在传统阈值模型中引入一些新的机制。从在线服务产品采纳行为的传播过程中可以发现，有两个基本的特征在之前有关阈值模型的研究中都被忽略了：i. 随机自发采纳过程。一些个体由于受到外部因素的影响会自发转变为1态，而这种外部因素的作用是随机的，它在任一时刻都可能影响某些节点的状态。ii. 在整个传播过程中，存在一些“免疫”的节点，他们可能出于各种原因（如对某一公司的厌恶等）而始终拒绝接受某个产品，即不受周围邻居节点的影响。Ruan等人研究了在这两种新的机制作用下社会传染的动力学行为[3]。在新的模型中，网络中的节点以比例r随机处于免疫态。这类节点不直接参与传播过程（因为他们不受其他节点的影响），但却起到阻碍作用（因为当个体周围存在免疫态节点时，阈值条件更难满足）。另一方面，每一时间步网络中处在0态的节点会以一定概率p自发转变为1态。这类创新者的出现可能会引发局部的级联效应，从而促进全局传播的发生。

 

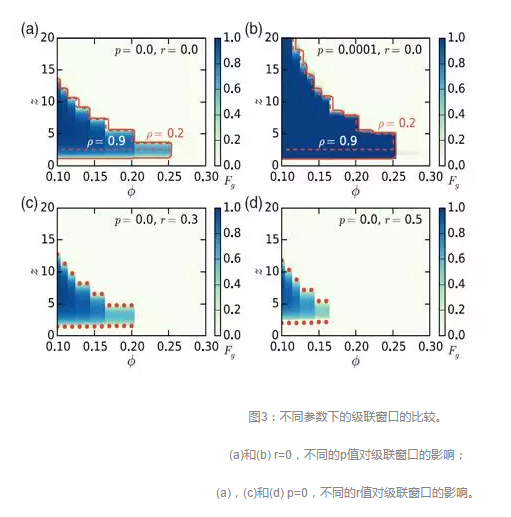
为了清楚地说明两种机制在社会传播过程中所起的作用，我们分别加以考虑。首先固定r=0而变化p值（即只考虑自发采纳过程的影响）。此时若p=0则回到经典的阈值模型。而当p>0（无论多小），对于t→∞，系统始终拥有单一的终态（全部节点都转变为1态）。为了方便比较，我们需要选取一个适当的时间窗口。图3a和b展示了t=100时，不同p值下级联窗口的大小。可以看出，p的增加使得全局级联传播的发生变得更加容易。其次我们固定p=0而变化r值（即只考虑免疫态节点的影响）。此时随着免疫比例r的增加，级联窗口不断缩小（见图3a,c和d）,意味着全局级联传播更不容易发生。

 

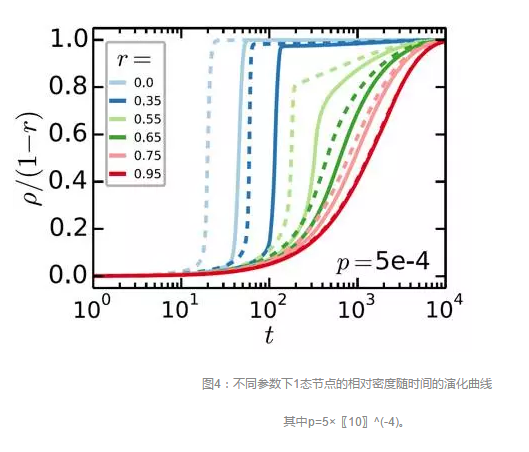
接下来我们考虑r,p>0的一般情形。此时在不同的免疫态比例下，系统从初态到终态（终态是单一的，即ρ/(1-r)→1）的演化过程会展现出极为不同的动力学特性。不失一般性，我们取p=5×〖10〗^(-4)，观察不同r值对传播动力学的影响。图4展示了1态节点的相对密度随时间的演化关系。可以看出，当r较小时，系统中1态节点的数目很快达到稳态；而当r较大时，1态节点的增长速度变得缓慢，需要很长时间才能到达稳态。这是因为当r较小时，随着创新者数量的增加，绝大多数个体都能被周围邻居所“诱发”转变为1态（通过满足阈值条件），这是一个快速的级联行为（因为个体一旦满足阈值条件，就立马转变其状态）。而当r较大时，节点很难满足阈值条件，几乎无法被周围邻居所“诱发”。此时随机自发转变机制占主导因素。由于自发转变是一个极其缓慢的过程（因为p一般来说很小），因此1态节点的数目相应地变化很慢。

 

进一步地，我们可以找到一个临界值r_c来区分快速传播与慢速传播的区域，即当r<r_c时，“诱发”机制占主导地位，系统能发生快速的级联传播；而当r>r_c时，自发转变机制占主导地位，此时传播行为变得缓慢。从图4可以观察到，这一转变过程是极其平缓的。我们可以通过几个不同的方法来确定r_c的值：例如通过观察稳态后创新者的比例随r的变化关系，或者ρ(t)演化曲线由凹变凸的转变，又或者是稳态时“诱导”集团的分布随r的变化关系等[3]。以ER随机网为例，当取参数z=7,ϕ=0.2,p=0.0005,N=〖10〗^4时（N为网络大小），可以得到r_c≈0.74。值得一提的是，随着免疫态比例r的增加，系统还会经历一个渗流变化的过程：即存在一个阈值r_，当r>r_时，由0态节点组成的集团会变得支离破碎，无法形成一个巨大的集团（因而无法实现全局级联传播，传播速度缓慢）。由渗流理论可知，r_=1-1/z=0.857（当网络中的节点以比例r随机处在免疫态时，有效平均度为z-zr，此时相变点在z-zr=1处）。r_c=0.74<r_意味着即使网络中存在由0态节点组成的巨大的集团，传播也可能是缓慢的（即缓慢传播不是单纯由网络拓扑结构变化引起的）。

 

参考文献：

[1] D. J. Watts, A simple model of global cascades on random networks, Proc. Natl. Acad. Sci. USA 99, 5766 (2002).

[2] M. Granovetter and R. Soong, Threshold models of diffusion and collective behavior, J. Math. Sociol 9, 165 (1983).

[3] Z. Ruan, G. Iniguez, M. Karsai, and J. Kertesz, Kinetics of social contagion, Phys. Rev. Lett. 115, 218702 (2015).

[4] M. Karsai, G. Iniguez, R. Kikas, K. Kaski and J. Kertesz, Local cascades induced global contagion: How heterogeneous thresholds, exogenous effects, and unconcerned behavior govern online adoption spreading. Sci. Rep. 6, 27178 (2016).