文 | 甘文聪 

 

全息引力理论是建立了无引力的量子场论（量子多体理论）与更高一维的引力理论之间的等价关系。但是直到现在，人们依然并不十分清楚如何从一个无引力的量子场论得到更高一维的引力理论。一个突破是2006年Ryu与Takayanagi发现的全息纠缠熵公式----他们建立了场论的纠缠熵与引力理论的最小面的等价关系。后来，人们发现本身被用来描述量子多体态的行为的张量网络具有与引力时空类似的几何结构。

 

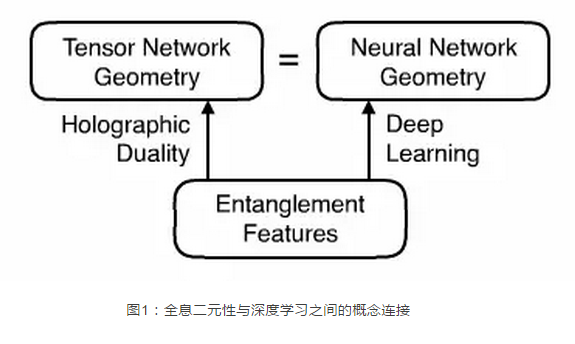
来自哈佛大学的集智科学家尤亦庄和来自斯坦福大学的祁晓亮、杨钊合作，在他们的最新论文Machine Learning Spatial Geometry from Entanglement Features（arXiv: 1709.01223）中提出寻找能描述量子多体系统的纠缠特征的最优随机张量网络（RTN）的问题可以等价为深度学习问题。因为深度学习恰恰是关于为了达到最优目标而调节神经网络结构（几何）的方法。正如论文中指出的，空间几何恰是编码纠缠特征的有效的方式。所以量子多体态的全息几何可以当做是从纠缠特征的深度学习中衍生出的神经网络几何。

 

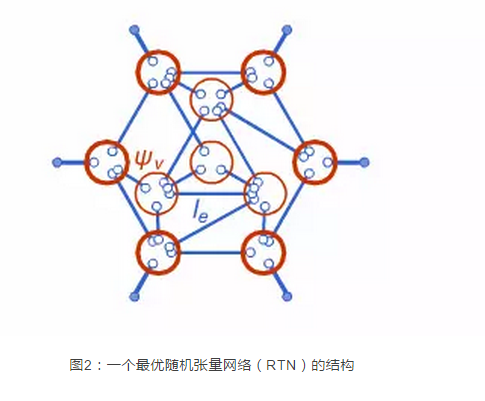
重整化群与全息对偶和深度学习均有紧密的联系，受此启发他们提出，全息几何可以从量子多体态的纠缠特征的深度学习中衍生出来。他们发展了一个具体的算法，称之为纠缠特征学习（EFL），此方法基于张量网络全息的随机张量网络（RTN）模型。他们展示了每一个RTN都可以被映射为玻尔兹曼机，该玻尔兹曼机由量子多体态的所有子区域的纠缠熵来训练。目标是构建能够最好重构该纠缠特征的最优RTN。他们展示了1维自由费米系统的EFL算法，并且发现当他们将费米系统的参数向无能隙临界点（CFT2）调节的时候，双曲几何（AdS3的空间几何）会自然的衍生出来。

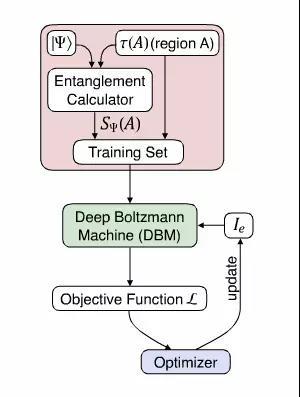
图3：纠缠特征学习（EFL）计算图

 

 

尤亦庄是集智科学家，现在在哈佛大学读博士后，早在09年的时候尤亦庄曾在集智俱乐部开过讲座，并且在2016年10月以及2017年7月时参加了集智俱乐部与凯风基金会共同举办的“网络、几何与机器学习”研读营活动，在活动中与来自世界名校的其余青年学者共同探讨，思想碰撞，他向大家展示了，基于平面图（planar graph）上Ising model的精确可解性，深度玻尔兹曼机（Deep Boltzmann Machine）可以映射为自由费米模型。量子多体系统不同区域之间的长程纠缠可以由隐层神经元的结构来刻画，而他通过深度学习的算法表明，临界点上的自由费米系统的纠缠特征对应的神经网络结构正是双曲几何。这正是他最新论文的核心观点。

 

 

“其实我们这项工作很大程度上也得益于研读营活动”尤亦庄博士在采访中谈到，“特别是我在研读营与另外两名集智科学家张潘和李嫣然的讨论，对我有很大的启发。我们在论文中也特别致谢了集智俱乐部和凯风基金会的支持。我希望我们的研读营能够继续办下去，能够吸引到更多优秀的年轻学者参与讨论，能够在讨论中激发出更多更好的研究成果。”

 

想要了解更多信息，可以阅读整篇论文Machine Learning Spatial Geometry from Entanglement Features（arXiv: 1709.01223）。