
凝聚态物理学家正尝试列举和分类所有可能的相。如果实现了完整的分类,不仅可以更好地解释目前为止自然界中已知的相,还可能指引新材料和新技术的发展方向。
编译:集智翻译组
来源:
原题:Physicists Aim to Classify All Possible Phases of Matter
在过去的三十年里,凝聚态物理学家发现了物质的相的崭新领域:相互作用的粒子涌现的集体态(emergent, collective states)。这些新的物质状态迥异于通常的固态、液态或气态。这些物相有些已经在实验室中实现,而另一些只是理论上可能存在。
上世纪80年代关于分数量子霍尔效应(fractional quantum Hall effect)的实验表明,在某些情况下,电子大量分裂成分数粒子(fractions of particles),在时空中留下发辫般的轨迹。在另一些情况下,电子可以是零质量的集体激发。比如,自旋粒子的晶格变成旋转的环、分叉的弦的流体,再者,原本处于绝缘状态的晶体,表面开始导电,即拓扑绝缘体。
另外,一种物相在2011年被认为是一种数学可能性的时候,震惊了相关领域的专家。这种物相是一种奇异的、像粒子一样的“分形子”(fracton),以分形的结构绑定在一起。
分数量子霍尔效应:
上文提及的2011年相关研究:
分形子:分形结构的、集体的量子化振动,是声子(phonon)的分形结构的类似物。声子是将平移对称性应用于薛定谔方程的势能,平移对称性是位置平移后保持不变的对称性,与之相对应,分形结构的自相似性是尺度变化下的不变性。
0.探索所有可能的相
如今,为了发展量子计算机,微软和其他机构的研究小组正竞相将量子信息编码进这些发辫状与环状的物相。
同时,就在最近,凝聚态物理学家在理解可能产生的不同集体行为背后的模式方面取得了重大进展,目的是列举和分类所有可能的物相。如果实现了完整的分类,不仅可以解释到目前为止自然界中已知的所有物相,而且还可能指引新材料和新技术的方向。
在众多理论物理学家的带领下,加上数学家的贡献,研究人员已将大量一维或二维空间可能出现的物相分类,方法是将物质与其拓扑结构联系起来。(拓扑,即描述球面、环面等形状不变性的数学。)
他们也开始探索三维物质在接近绝对零度时可能出现的物相,这是目前研究中的空白地带。
将量子信息编码进相:
凝聚态物理学家Michael Zaletel:
“科学家寻求的并非一个特别的物理定律,而是所有可能性的空间。某种程度上,这是更加美丽而深刻的想法。” 普林斯顿大学的凝聚态物理学家Michael Zaletel说,或许令人惊讶的是,所有连续相(consistent phase)的空间本身是一个数学对象,“有着如此令人难以置信的丰富结构,我们认为在一维和二维,它最终与这些美丽的拓扑结构一一对应。”

在物相的图景中,“所有的可能性都能够被有规律的分类,”哈佛大学的 Ashvin Vishwanath 说,“一切似乎都是可以被解释的”——这又似乎太过巧合,让他感到困惑。
列举物质的相可能如同“集邮”,“每一张邮票只有一点不同,且不同的邮票之间彼此没有联系”。相反,物相的分类“更像是元素周期表,有很多元素,但元素都可以被划分入人们可以理解的不同的类。”
尽管对涌现粒子的行为进行分类看似并不具有根本的重要性,但包括麻省理工学院的文小刚在内的一些专家却认为,关于涌现的物相的物理规律表明,基本粒子本身可能是从量子信息纠缠位元的底层网络(underlying network)产生,文小刚称之为“量子比特海”(qubit ocean)。
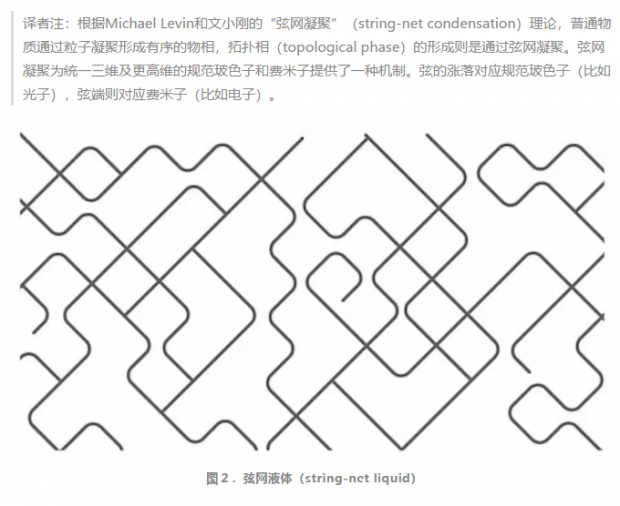
例如,一种名为“弦网液体”(string-net liquid)的物相,可以出现在三维的量子比特系统中,具有与所有已知的基本粒子看起来相似的激发。文小刚说,“真正的电子和真正的光子可能只是弦网的涨落。”
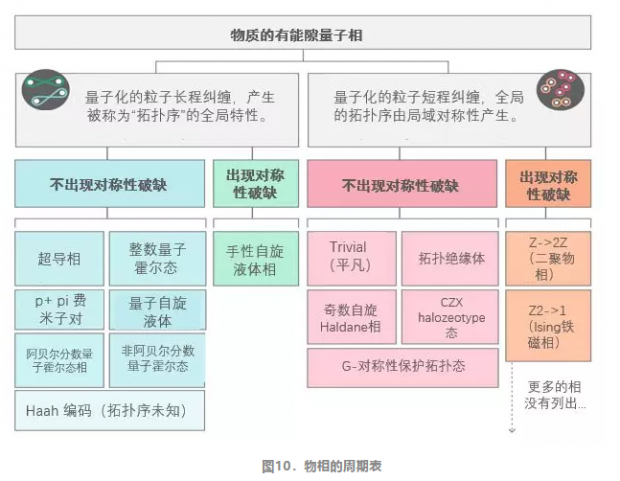
1.从对称性到“拓扑序”
——一个新的拓扑顺序
在这些绝对零度的物相出现之前,物理学家们曾认为,他们已经弄懂了所有的物相。在二十世纪五十年代,只要通过将相变过程描述成一种对称性的破缺(break of symmetry),就可以解释当水结成冰时发生了什么: 液态水在原子尺度上具有旋转对称性,即在每个方向上看起来都一样,而冰中的水分子锁定在晶体的行和列中。

1982年,事情发生了变化,在超低温条件下,二维电子气的分数量子霍尔态(fractional quantum Hall state)这一新的物相被发现。这些奇特的物质状态,具有分数的电子电荷,沿着系统的边缘以分数的步伐单向前行。
不同的分数量子霍尔态具有相同的对称性,因而不能用朗道的对称性破缺理论来描述,它们代表了一种新的序。
“当时没有办法用不同的对称性来区分这些物相,” 文小刚说,“需要一个新的范式“。在1989年,文小刚想象如同分数量子霍尔态那样的相,不是出现在平面上,而是在不同的拓扑流形(topological manifold)——比如像球面或环面的表面一样连通的空间上。

拓扑涉及这些空间全局的、不变的属性, 不会因局域形变而改变。对一个拓扑学家而言,仅仅通过改变物体表面的形状,他可以把一个甜甜圈变成一个咖啡杯,因为这两种物体的表面都有一个孔洞(甜甜圈的中心和咖啡杯的手柄),在拓扑结构上是等同的环面。相反地,他可以任意拉伸或挤压,但即便是最具可塑性的甜甜圈也会“拒绝”成为一块饼干。
文小刚发现,不同的拓扑结构揭示了绝对零度相的新特性。他创造了“拓扑序”(topological order)这一新名词来描述这些物相的本质。其他理论物理学家也在揭示物质的相与拓扑的联系。随着许多更奇特的物相被发现——事情变得清楚无疑,那就是拓扑与对称性为分类提供了很好的组织架构。
“拓扑序”论文:~wen/pub/topo.pdf
拓扑相(topological phase)只在接近绝对零度时出现,因为只有在如此低的温度下,粒子系统才能回复到它们最低能量的量子“基态”。在基态,与粒子特性相关的微妙相互作用——在较高温度下被破坏的效应——将处于全局量子纠缠模式的粒子连接起来。粒子并非只有单独的数学描述,还是一个更复杂的函数的组成部分。函数同时描述所有粒子,通常是以全新的粒子出现,作为全局的物相的激发。出现的长程纠缠模式是拓扑的,不受局域变化的影响,就像流形中孔洞的数目一样。
2.根据拓扑结构分类物质的相
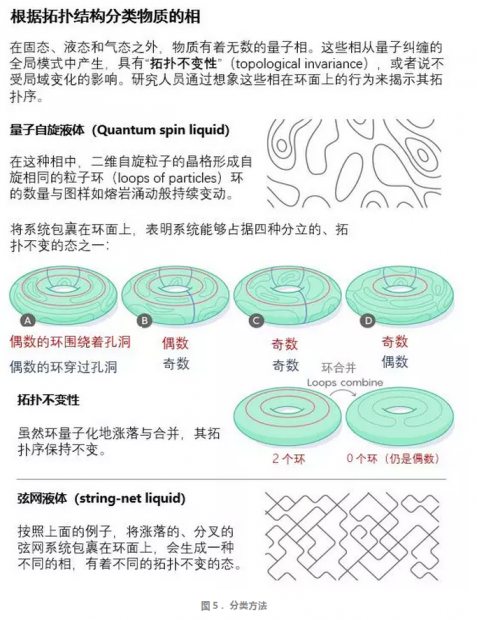
考虑系统中最简单的拓扑相——所谓的“量子自旋液体”——由二维的“自旋”晶格组成,或是由指向上下两个不同方向的粒子,又或是以某种概率同时指向上下两个方向的粒子组成。

在绝对零度时,自旋液体中所有自旋向下的粒子形成弦(string of spins),这些弦形成闭合的环。随着自旋方向量子化地涨落,整个材料中环的图样也不断变化:粒子自旋向下的环合并成更大的环,或者分成较小的环。在量子自旋液体中,系统的基态是所有可能的环形图样的量子叠加。
为了理解作为一种拓扑序的纠缠模式,不妨像文小刚所做的那样,想象量子自旋液体包裹在环面上,一些环围绕着圆环的孔洞,一些环穿过孔洞。由于这些围绕孔洞的环,量子自旋液体不是以所有环形图样叠加而成的单一基态存在,而是处于四种分立的基态之一,这四种基态对应于环形图样的四种不同叠加态。
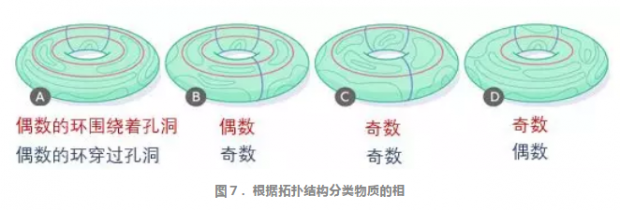
如图7所示,基态A是偶数的环围绕孔洞、偶数的环穿过孔洞的所有可能的环形图样的叠加。基态B有着偶数的环围绕孔洞、奇数的环穿过孔洞;基态C和D分别对应于奇数-偶数,奇数-奇数的缠绕。
不管系统处于哪个基态中,这个态是稳定的,即使环形图样存在局域涨落。
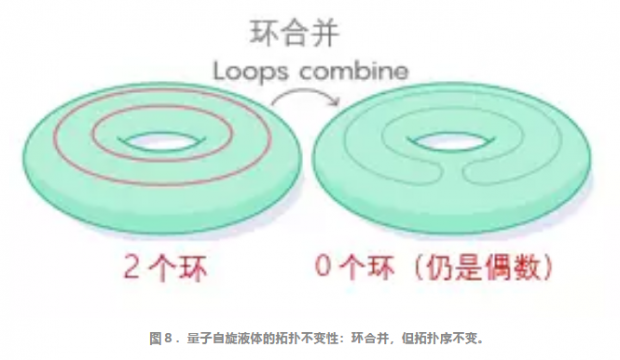
例如,如果自旋液体有偶数的环围绕环面的孔洞,两个环可能接触而合并成一个不再围绕孔洞的环。环的数量减少了两个,但仍然是偶数。按照Z2拓扑不变量分类(奇偶分类),只有奇数和偶数两种拓扑上不等价的结构,因此,系统的拓扑序不变。系统的基态不受局域变化的影响,具有拓扑不变性。
未来的量子计算机可以利用这种不变的性质。具有四个不受局域形变(local deformation)或环境干扰(environmental error)影响的拓扑基态,“提供了一种存储量子信息的方法,因为位元可以存在于基态,” Zaletel解释说,他曾研究过自旋液体和其他量子相的拓扑性质。
像自旋液体这样的系统并不真的需要环绕一个环面以拥有拓扑保护的基态(topologically protected ground state)。研究人员最喜欢的对象其实是Toric 编码(Toric code),这是加州理工学院的凝聚态理论物理学家 Alexei Kitaev 在1997年从理论上构建的一种物相,并在过去的十年里在实验上实现。Toric 编码是一种拓扑量子纠错码(topological quantum error correcting code),是定义在二维自旋晶格上的稳定子码(stabilizer code)的例子。
凝聚态理论物理学家 Alexei Kitaev:
Toric 编码应用周期性边界条件,自旋粒子形成的环本质上能够从系统的边缘移出,并从相反的一侧重新进入,允许它们环绕系统,就像围绕环面孔洞的环一样,因而Toric 编码具有平移不变性,可以存在于平面上,并且仍然保持存在于环面上的多个基态。“我们知道如何在环面上的基态特性之间进行转换,也知道粒子的行为。”Zaletel说。

自旋液体还可以形成其它物相,在其中,自旋粒子并不形成闭合的环,而是形成分叉的弦的网状结构,这就是弦网液体。根据文小刚的理论,从三维的量子比特海开始,自旋液体“能产生粒子物理的标准模型”。
3.相的宇宙——
一维、二维与三维
2009年和2010年,几个小组的研究完成了对一维有“能隙”物质相的分类,例如粒子链。有能隙相(gapped phase)的基态具有如下特性:最低能量态足够地远离高能量态,或者说与高能量态存在能隙,所以系统稳定地处于最低能量的基态。只有有能隙量子相具有明确的粒子形式的激发。无能隙相(gapless phase)如同漩涡状的物质迷雾或者量子汤一般,在相的图景中,很大程度上仍然是未知的领域。
一维玻色子链只有一个有能隙的拓扑相。这个物相是普林斯顿大学的理论物理学家Duncan Haldane首次研究的,他因为数十年关于拓扑相的工作,与David Thouless和J. Michael Kosterlitz一起获得了2016诺贝尔奖。自旋链在两端产生半自旋粒子。一维费米子链具有两个有能隙的拓扑相。
这些一维粒子链的拓扑序不是源于长程量子纠缠(long-range quantum entanglement),而是来自作用于近邻粒子之间的局域对称性(local symmetry)。
它们被称为“对称性保护拓扑相”(symmetry-protected topological phase),对应于“上同调群的余圈”(cocycle of the cohomology group)。在群论中,上同调(cohomology)是一种对拓扑空间赋予代数不变量的方法,是对余圈(cocycle)等数学对象的抽象研究。上同调群的余圈是一种类似于流形中的孔洞数量的不变量。
二维空间的物相更为丰富和有趣。它们可以具有与量子纠缠的长程模式相关的拓扑序,如自旋液体中环形图样的涨落,这被一些专家认为是“真正的”拓扑序。
在过去的几年中,研究人员已经证明,这些纠缠模式对应于被称为张量范畴(tensor category)的拓扑结构, 它列举了物体可以融合或编织在一起的不同方法。马德里康普鲁滕塞大学(Complutense University of Madrid)的David Pérez-García说,“张量范畴提供了一种描述粒子以一致的方式融合或编织的方法。”
David Pérez-García教授简介:
下文提及的2010年的相关研究:
Pérez-García及其他研究人员试图从数学上证明,对于二维有能隙拓扑相的已知分类是完备的。他在2010年帮助完成了一维情况的分类——至少在人们普遍认为的假设之下,即这些物相总是被量子场论很好地近似。量子场论的数学描述把粒子的环境看成是平滑的。
Pérez-García说,“人们推测,张量范畴将涵盖所有的二维相,但目前还没有从数学上证明。当然,如果能证明这些并非全部的物相,那就更有趣了。奇特的事物总是有趣的,因为其中蕴涵着新的物理,而且可能有用。”
无能隙量子相代表了另一个可以探索的、充满可能性的领域,然而这些复杂的物质迷雾始终难以被现有的理论方法描述。麻省理工学院的凝聚态物理学家Senthil Todadri说,“粒子的语言是无用的,我们正面临最大的挑战。”
凝聚态物理学家Senthil Todadri:
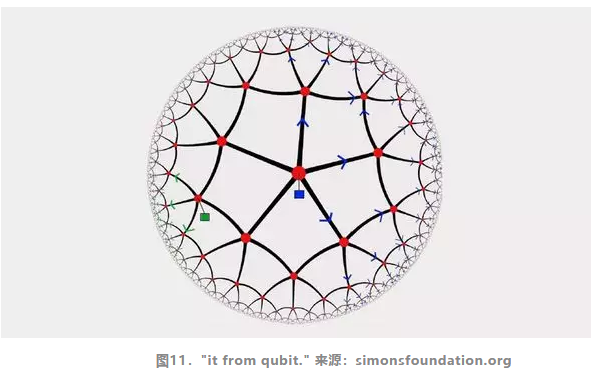
无能隙量子相是寻求理解高温超导的主要障碍。它们还阻碍了量子引力研究人员“it from qubit”(一切源自量子比特)的运动,这些研究人员认为,不仅基本粒子,包括时空和引力,都来源于某种底层量子比特海中的纠缠模式。马里兰大学的理论物理学家Brian Swingle说,“在it from qubit中,我们花费了大量时间研究无能隙量子相,因为根据现阶段的理解,引力正来源于此。” 一些研究人员试图利用数学对偶将量子汤的图像转换成高一个维度的等价的粒子描述。对此,Todadri说,“一切应该以探索的精神来看待。”
在三维空间进行着甚至更为热情的探索。已经清楚的是,当自旋或其他粒子从自身所在的链条或平面脱离,并填满真实的三维空间时,会出现难以想象的量子纠缠模式。“到目前为止,在三维空间,有些东西逃脱出了张量范畴的图像。这种激发十分奇怪,超出了我们现有的理论框架。”Pérez-García说。
4.Haah编码 (The Haah Code)
最疯狂的三维相出现在七年前。加州理工大学一位有天赋的研究生,Jeongwan Haah在计算机上搜索寻找“ 梦想编码”方案时,发现了这个物相。这个物相的量子基态是如此稳定,即使在室温下,也可以用来安全地进行量子存储。

为此,Haah不得不求助于三维物质。在二维拓扑相(如toric 编码)中,一个重要的错误来源是“弦算符”(stringlike operator):对系统的扰动导致新的自旋弦意外地形成。这些弦有时会围绕环面孔洞形成新的环,使环的数量从偶数变为奇数或者相反,将toric 编码转换为其它三个量子基态之一。因为弦不受控制地增长,并环绕物体,专家们认为,在二维空间不可能实现好的量子存储。
Haah编写了一个算法来搜索三维相,以避免通常的弦算符。计算机给出了17种确切的解答方案,接着他开始亲自研究:其中四种物相被证实没有弦算符,当中对称性最高的那个现在被称为Haah 编码。
Haah 编码对于量子存储有潜在的用途,但也非常怪异。加州理工大学的凝聚态物理学家陈谐回忆起她听闻这个消息时的情景,那个时候离Haah令人迷惑的发现只有一两个月,她还是一名研究生,“每个人都非常震惊,我们不知道拿它怎么办。而现在多年过去了,情况一直如此。”
Haah 编码的数学形式相对简单:一个两项的能量公式的解,描述了立方晶格中与八个最近邻相互作用的自旋粒子。然而生成的物相超出了我们想象力的极限,Todadri 说。
Haah 编码的特点是类似粒子的实体,分形子(fracton)。分形子是非液态的,且固定在晶格的位置上,不同于量子自旋液体中的环形图样。只有当晶格的位点构成分形模式时,粒子(在分形晶格中是分形子)才能在这些位点之间跳跃。也就是说,为了使分形子交换位置,必须向系统,比如连接四个分形子的正四面体的每个角注入能量;但是当系统放大的时候,原本看似只是点状的角会随之放大,成为一个小的正四面体,必须向这些小正四面体的每个角也注入能量。在更精细的尺度上,会看到更小的正四面体,如此层层深入,直到晶格最精细的尺度。

这种分形行为意味着Haah 编码永远不会“忘记”组成它的底层晶格,也永远无法用一个平滑的晶格描述来近似,如量子场论当中那样。此外,Haah 编码的基态数量随着底层晶格的规模增长,这是绝对的非拓扑性质。(拓扑结构,比如一个环面,伸展后仍然是一个环面,并不随尺度改变。)
Haah 编码的量子态非常安全,因为一个完全命中所有晶格位点的“分形算符”(fractal operator)不太可能随机出现。专家表示,可实现的Haah 编码版本将具有很大的技术层面的意义。
Haah相也激发了理论思考。Haah一直在促进事情的发展。2015年,他和麻省理工学院的两名合作者发现了现在被称为“分形子模型”(fracton model)的一类物相的许多实例,这是Haah 编码较为简单的类似物。(这个族的第一个模型,Chamon模型,是由波士顿大学的Claudio Chamon于2005年引入的。)
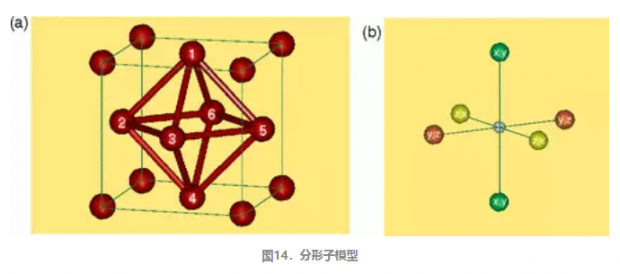
从那以后,陈谐和其他人一直致力于研究这些分形子系统的拓扑结构,其中一些系统允许粒子在三维体积范围内沿着线或平面移动,这或许有助于对概念的理解,或者更容易在实验中实现。
Hahh实例研究:
模型引入:
陈协后续研究:
更易在实验室实现的系统:
Haah 编码“正在为奇特的的事物敞开大门,” 陈谐说,“这说明我们对三维和更高维度所知是多么少!因为我们对正在发生的事情还没有系统的图像,可能有很多东西等待着我们去探索。”
还没有人知道Haah 编码及其类似方法在可能的物相的图景中处于什么位置,或者这个可能性的空间有多大。据Todadri说,人们已经在对最简单的有能隙三维相的分类方面取得进展,但是在完整的分类计划能够开始之前,需要对三维的相进行更多的探索。他说,很清楚的是,“当有能隙物质相的分类在三维空间开始时,将不得不面对Haah最先发现的这些怪异的可能性。”
许多研究人员认为,新的分类概念,甚至全新的框架,对于捕捉Haah 编码的分形性质,以及揭示三维量子物质的所有可能性可能是必要的。
文小刚说,“需要新的理论,新的思维方式。”他认为,对于长程量子纠缠的非液态模式,我们或许需要新的图像。“我们有一些模糊的想法,但没有非常系统的数学去实现。我们可以感觉到它大概是什么样子,却仍然缺乏详细的系统。然而这令人兴奋。”
参考译名列表
fracton 分形子
Toric code Toric 编码
Haah code Haah 编码
stringlike operator 弦算符
gapless phase 无能隙相
gapped phase 有能隙相
symmetry-protected topological phase 对称性保护拓扑相
topologically protected ground state 拓扑保护基态
chiral spin liquid phase 手性自旋液体相
CZX halozeotype state CZX halozeotype 态
Abelian fractional Quantum Hall state 阿贝尔分数量子霍尔态
spin liquid 自旋液体
string-net condensation 弦网凝聚
string-net liquid 弦网液体
quantum order 量子序
topological order 拓扑序
topological phase 拓扑相
cocycle 余圈
cohomology group 上同调群
tensor category 张量范畴
topological quantum error correcting code 拓扑量子纠错码
stabilizer code 稳定子码
翻译:梁金
审校:黄金龙、陈星强
编辑:王怡蔺
原文:
0
推荐



 京公网安备 11010502034662号
京公网安备 11010502034662号 