导语
在没有任何先验信息的情况,能不能利用机器学习的方法,学会某种“窥一斑而知全豹”的方法,找到那些适当的自由度来进行后续的重整化操作呢?近期发表在 Nature 的一篇论文讨论了这一问题,下面是傅渥成对这篇论文的解读。
文 | 傅渥成
论文地址:
论文题目:
Mutual information, neural networks and the renormalization group
(一)背景介绍
对于一个有大量自由度的复杂系统,在对其进行研究时,我们会希望找出其中的那些真正重要的自由度。例如,在统计学习问题中,我们会常常用降维的方法来对系统的自由度进行约简,构造出一些新的主要变量。而在物理学中,我们用重整化(Renormalization)的思路来求解这一问题。
重整化是物理学中面对发散问题时的一种重要方法,在统计物理和量子场论中有许多非常重要的应用。重整化方法希望通过在不同尺度下的标度变换,找到处在临界态的物理系统在标度变换中的一些不变性。
用一个粗糙的例子来说明降维方法和重整化方法的不同。假如现在有一棵树,要完整描述一棵树非常复杂。用降维的方法,我们找到了这棵树的主成分方向(竖直方向),于是我们用树的“高度”来简化对一棵树的复杂描述。而重整化方法关注的是树的自相似特征,因为树的每一个分支与整棵树的性状是相似的,而分支又与更小的分支相似,以此类推。重整化群想要提取的就是隐藏在这些迭代操作中的特征,希望挖掘出系统在不同的尺度之间的关系。
正因为如此,重整化群找到的是这个系统中“适当”(relevance)的自由度[1],一旦找到了这些自由度,我们就可以“窥一斑而知全豹”,利用这些自由度描述那些支配系统在较大尺度上的行为的特征,这些自由度不会受到噪声和局部涨落的影响。

深度学习的方法与重整化群有许多相似之处。
首先从表面上来看,以基于卷积神经网络(CNN)的人脸识别为例,在这样的一个神经网络上,较为低级的层级首先提取的是图片中一些边缘和界面的特征,随着层级的提高,图片中一些纹理的特征可能会显现,而随着层级继续提高,一些具体的对象将会显现,例如眼睛、鼻子、耳朵等等,再到更高层时,整个人脸的特征也就被提取了出来。
在一个深度神经网络上,较高层的特征是低层特征的组合,而随着神经网络从低层到高层,其提取的特征液越来越抽象、越来越涉及「整体」的性质。从更深层次的角度来看,深度神经网络不是简单的神经网络的堆砌,而是能真正从数据中找到数据中的一些隐藏的对称性和约束。这是非常重要的一个性质。要知道,深度学习的网络模型容量巨大、参数众多,而“四个参数就能画一头大象”,所以深度学习真正的神奇之处不在于深度学习能解决多么困难的问题,而在于深度神经网络经过训练能够较稳定地提取特征、并在实践中表现出较好的泛化能力。
这意味着深度学习提取到的特征会是那些不受噪声影响的慢变量,这与重整化的思路也是一致的,这些“慢变量”也就是我们前面提到的“适当的”自由度。深度学习与重整化方法的这种相似性目前已经吸引了许多来自不同背景的科学家们的注意,近年来也有许多工作尝试在重整化群和深度学习之间建立联系。
(二)文章的核心思路
我们今天要介绍的这一篇文章(Nat. Phys. 2018. 14: 578-582),从一个全新的角度切入了机器学习和重整化的问题。作者们思考的问题是:在没有任何先验信息的情况,能不能利用机器学习的方法,学会某种“窥一斑而知全豹”的方法,找到那些适当的自由度来进行后续的重整化操作呢?
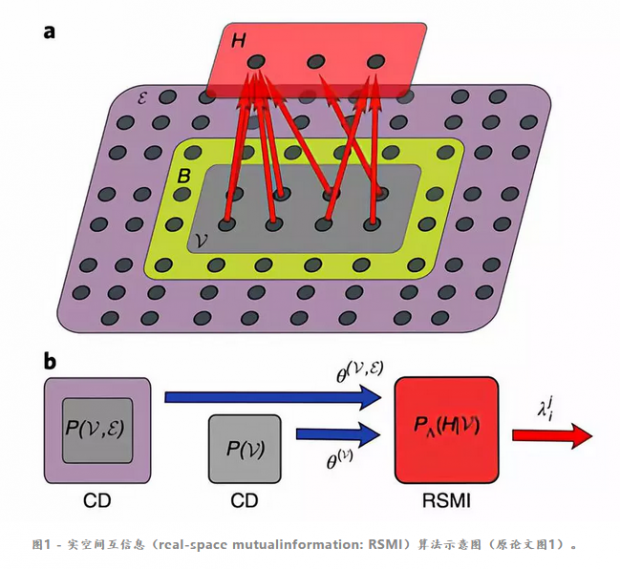
作者们考虑的是如上图所示的一个经典系统,这个系统被分成三部分:第一部分是可见(V)的部分,也就是我们所说的“一斑”,这一部分的信息可以被隐藏层 H提取;构成系统的第二部分是环境(ε),这是我们想要了解的“全豹”;在这二者之间存在着一个缓冲区(B)。
所谓的“窥一斑”,其实也就是指从可见的部分中提取出信息,即在给定 V 的情况下,得到条件概率分布P(H|V)。怎样来理解条件概率分布P(H|V)呢?如果H的节点数目小于V,我们可以说,P(H|V)是对V的一个“粗粒化”的描述,这种粗粒化描述的方法与参数Λ有关(这一参数的物理意义和求解,我们会在后面解释)。
如果这种粗粒化的描述可以真的让我们“窥一斑而知全豹”,那么也就是说,我们从这“一斑”中获取的信息,与“全豹”中获取的信息是能重合的。换句话说,上述方法得到的P(H|V)可以使得隐藏层提取的信息 H 跟环境中实际的信息ε之间的互信息(原文公式1)最大化。
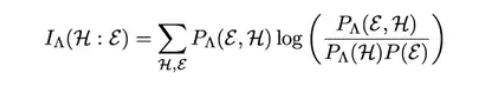
(三)求解过程
好了,到这里为止,要求解的问题已经被定义清楚了。不过,这个问题的求解却并不简单,这是因为“最优的概率分布”实在是参数太多、太难描述了。为了简化这一问题,作者们用了限制玻尔兹曼机(RBM)来简化这一描述。
我们以隐藏层H和可见层V联合概率分布为例来介绍,在RBM中,相互作用只存在于H和V之间,隐藏层H内部没有相互作用,可见层V内部也没有相互作用[2],这样,就可以把V和H的联合分布写成一个能量函数的玻尔兹曼因子的形式(原文公式2)。
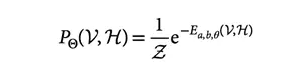
在整个问题的求解过程中,我们一共需要面对三个不同的RBM(如图1b中所示):第一个RBM是用来计算可见层V和环境之间的ε联合概率分布的;第二个RBM是用来计算可见层V的概率分布的,这两个RBM都用对比散度(contrastive divergence: CD)算法训练,训练完成后,这两个RBM使用的参数被传到了第三个RBM。而这第三个RBM就是前面提到的、用来计算隐藏层H和可见层V之间概率分布的RBM,这个RBM也就是作者们所提出的“实空间互信息(RSMI)算法”的核心了。
在优化的过程中,不断被优化的参数是Λ。我们前面已经提到,参数Λ刻画的是粗粒化描述的方法,在RBM中,它实际上描述的就是隐藏层H和可见层V之间的耦合(附录公式一)。
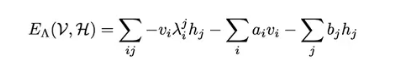
因为RSMI训练的目的是希望隐藏层H 跟环境信息ε 的互信息最大化,找到此时最佳的参数Λ,也就找到了将显层的数据粗粒化的方法,这个方法所找到的,就是重整化群中的适当自由度。因为这个优化的过程是一个最大化问题,因此可以直接采用随机梯度下降的方法来训练。
点击此处更多了解RBM内容:用人工神经网络解决量子多体问题
(四)主要结果
作者们首先用二维Ising模型对RSMI算法的有效性进行了验证。在二维Ising模型的重整化中,最常用的一种粗粒化的方法就是构造“块自旋”,这一方法最早由Kadanoff提出(如下图所示)。
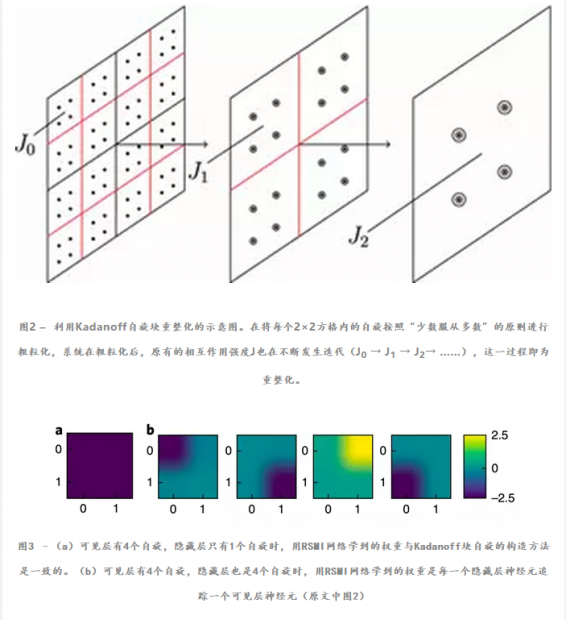
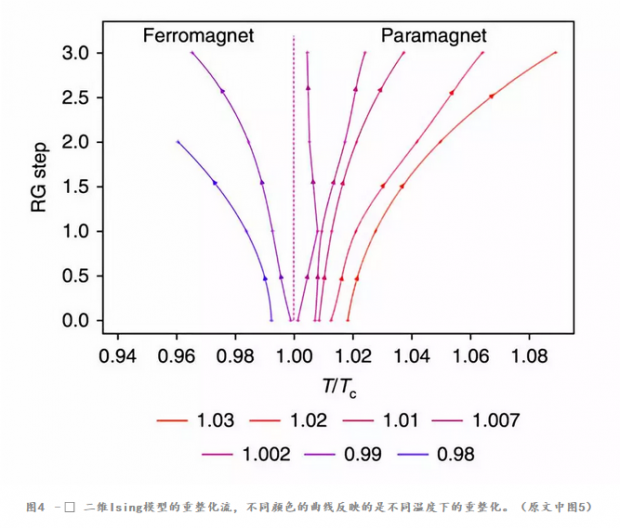
当用RSMI方法来学习Ising模型时,有意思的是,系统自己学出了Kadanoff的块自旋构造(如图3所示),利用计算的结果,可以进行重整化(如图4)所示。根据重整化流计算得到的临界指数也与实际二维Ising模型一致。
除此以外,作者们还用这一方法对 dimer 模型(如原文中图3、图4所示)进行了研究,之所以选择 dimer模型,原因在于,Ising 模型经过块重整后、得到的是与自身形式完全相同粗粒化表示,而dimer模型得到的则是完全不同的形式。作者们发现RSMI方法在 dimer 模型的重整化中也能有很好的表现,这说明RSMI方法能在各种场合都能找到合适的重整化操作、提取出适当的自由度。
(五)延伸讨论
正如作者们所说,这篇文章所引入的这种方法对于分析很多复杂统计物理体系(例如玻璃体系、无序体系、量子体系等)、提取出这些体系中的适当自由度可能对于解决这些复杂问题起到重要的作用。
这篇文章只是给出了机器学习来解决重整化问题的一种方法,在这篇文章以外,还有很多其他同类型的工作(例如中科院物理所王磊等人的文章 arXiv: 1802.02840)。而在作者们的视野以外,我们还可以对这篇文章所介绍的方法有新的理解。这篇文章基于“互信息”的处理方法与“信息瓶颈(information bottleneck)”的方法有相似之处,只不过作者们在信息的压缩部分利用了RBM的性质。
另外,如果我们把重整化群看成就是一个机器学习系统,那么“学习重整化群”某种程度上就是一个“元学习”(Meta Learning / Learningto learn)的问题了。此外,这篇文章的视角也可以帮助我们从信息处理的角度来理解重整化群,相应的框架对于理解像生物对环境的适应等问题也有一定的借鉴意义。
注释
[1] “Relevance”一词更常见的翻译是“关联/相关”,然而我们在这里用“适当”一词来翻译,主要是为了与“correlation”作区分。
[2] 这是由于引入了“缓冲区”,导致 V内部的关联被消除了,更多关于缓冲区的讨论可以参考原论文附录。
编辑:王怡蔺
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 