编译：集智翻译组

来源：www.quantamagazine.org

雪城大学（Syracuse University）物理学副教授Lisa Manning因成功从物理学角度解释发育生物学而广受赞誉。正如她已经证明的那样，对玻璃材料的数学描述可以用于预测胚胎组织细胞的动态。她说：“玻璃物理学可以有如此之多的应用，这正是它的独特之处”。

在进入加州大学圣塔芭芭拉分校（University of California, Santa Barbara）开始研究生学习之前的那个夏天，在那拥堵不堪的高速公路上，正是那些走走停停的汽车，吸引了Lisa Manning，也第一次引领她迈入了自己喜欢的物理领域。她对车流中的涌现行为产生了兴趣——“如何从车辆间的局部规则入手，发现交通中拥堵的波动情况 ”她说。但直到2008年获得了物理学博士学位后，Manning才开始将这种热情应用于生物学问题。

在普林斯顿大学（Princeton University）博士后研究期间，Manning了解到所谓的“差异粘附假说”—这是20世纪60年代发展起来的一个理论，解释了胚胎中的细胞群如何运动，并根据表面张力等因素进行分类。“考虑到生物体如此之高的复杂性，这样一个简单的物理想法竟可以解释如此多的生物数据，确实令人惊讶。”Manning感叹道，而此时她已经成为雪城大学的副教授。 “这项工作让我确信，在生物学中这种[基于物理学的]思维或许能够占一席之地。”

她的灵感来自于玻璃动力学，这些无序固体物质的行为类似于流体。 Manning发现，我们身体的组织在许多方面都有相同的表现。因此，凭借从玻璃物理学中获得的发现，她已经能够对组织中细胞间相互作用的机制进行建模，并揭示它们与发育和疾病的相关性。尽管 Manning的职业生涯还刚刚起步，但她的研究、教学以及她在科学、技术和医学领域为为吸纳和支持女性所做的努力，已经获得了无数奖项。用一位同事的话来说，她是“一颗冉冉升起的新星”。（编者按:发行《Quanta》杂志的西蒙斯基金会对Manning的工作提供了部分资助。）

《Quanta》杂志最近采访了Manning，谈到了细胞群如何在流态和固态之间移动和转变，它们如何在胚胎发育过程中保持其器官形成的边界，以及细胞分裂如何潜在地导致癌症等疾病。为了清晰起见，访谈已经被精简和编辑。

让我们从简单的部分开始。什么是玻璃问题?

要把流体变成固体，你可以在冰箱里放一杯水，等它变成冰。对于物理学家来说，这是一个很容易理解的过程:我们知道，流体中的分子都混杂在一起，系统能变得坚硬或者变为固体，是因为这些分子变得有序。

从微观层次上来看，玻璃材料的流态和固态是相同的，这也是在过去50年间一直困扰学界的一个谜团，即玻璃的那神奇的固液转变究竟是怎么发生的。通常，刚性与对称性的破坏有关:流体中的原子在任何地方看起来都是一样的，而在固态下，存在一些与有序晶格相关的特殊方向。仅就玻璃而言，目前并不清楚是哪一种对称性被打破，也不清楚刚性是如何产生的。

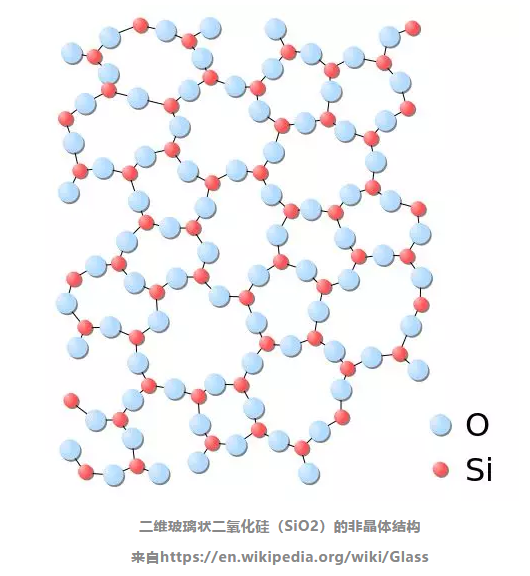
“玻璃物理学有其特殊之处，因为它有很多应用。……它几乎无处不在：进化模式，磁铁模式，社交网络动态模式。”

你谈到了玻璃问题在人工智能和大脑网络、蛋白质折叠和形态发生等很多领域都有类似的应用。但是，你刚刚的描述似乎与人工智能相去甚远。这两者之间有什么联系呢？

我们认为，在玻璃系统中，之所以出现了很多有趣的性质，是因为存在所谓的复杂势能图景。如果你把整个系统的总能量看成是原子所在位置的函数，那么在无序的玻璃中，这种图景极度复杂的。

事实证明，用于深度学习和优化的神经网络，与玻璃之间拥有相当多的相同属性。你可以把网络的节点看作粒子，将它们之间的连接视为粒子之间的键。这样一来，神经网络和玻璃就有了几乎具备相同性质的复杂潜在势能图景。例如，关于神经网络中状态间的能量屏障问题，就与玻璃材料材料变为流态的可能性相关。所以我们希望了解玻璃的一些特性，从而帮助我们理解神经网络中的优化。

材料科学与其他领域如此相关，很常见吗?

玻璃物理学的独特之处在于它有如此之多的应用。玻璃和蛋白质折叠之间有一种古老的联系，相关研究可以追溯到20世纪80年代。现在，它几乎无处不在:进化模式，磁铁模式和社交网络动态模式中，都有玻璃物理学的身影。我想说，这是因为，对于一个极度无序的系统而言，玻璃是一个非常简单的模型。所有这些都是节点组成的网络，而节点之间的连接是无序的。

那么，如何从这个物理问题的角度阐述胚胎发生、发育过程中器官形成的问题呢?

令人惊讶的是，在发育过程中，尤其是在胚胎开始形成不同层次的早期阶段，细胞必须在相对较长的距离内相互流动。但是，在发育的后期阶段，作为一个成年人，动物必须表现得更像固体一样来支持行走和运动。

这意味着细胞群必须相当有规律地执行一个基因程序，从混杂在一起容易相互移动的流动状态开始，变成一个位置固定的系统。与此同时，你可以看到相反的情况，即组织可以发生液化，在伤口愈合中，细胞必须移动以停止损伤，或者在癌症中，癌细胞必须离开肿瘤从而转移。在单细胞层面上，所有这些的指令都在DNA中。那么在组织层面上，单个细胞如何改变一群细胞的整体力学特性呢?

雪城大学的物理学家Lisa Manning描述了玻璃材料的物理特性帮助我们解释了某些器官在胚胎发育过程中如何保持正确的形状。

——《Quanta》杂志Jennifer May 

玻璃转变的模型通常是基于分子或粒子的，这意味着相互作用取决于一个原子与另一个原子之间的距离。但是我们对融合胚胎组织很感兴趣，融合意味着细胞之间没有缝隙或重叠。这就表明我们没有改变任何与流态-固态转变有关的变量，比如温度或者粒子密度。如何在一个没有这些性质的系统中得到流态-固态的转换?

我们采用了现有的顶点模型，它将二维空间中的细胞紧密地堆积在一起，像多边形的瓷砖一样，每个顶点都随着表面张力的作用而运动。我们使用这个模型来检查属性，比如物理状态之间的能量屏障，或者细胞移动的困难程度。组织系统中的这些特性，与我们在普通材料中观察到的典型的玻璃转变的特征相同。



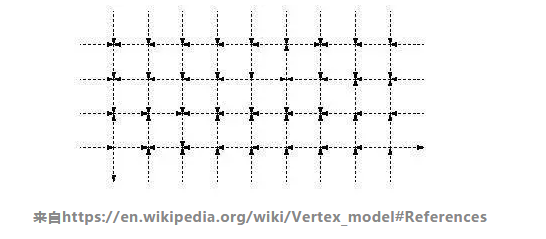
“单个细胞在组织水平上如何改变一群细胞的整体力学性质?”

通过研究这种转变，你对发育有什么见解?

我们想要了解器官在发育过程中是如何形成的，因为如果它们在发育中出现错误，就会导致先天性疾病。我们的一个假设是，某些器官在组织形成时，会主动地穿过组织。在一篇我们最近在arxiv.org上发表的论文中，我们提出，在器官运动的过程中，施加在一个器官上的机械流体力，足以改变细胞的形状，从而帮助器官发挥功能。事实上，器官通过一种更像流体或更像固体的物质帮助器官保持正常形成并发挥作用。在这篇论文中，我们观察了斑马鱼的器官（它构成了左右不对称的器官），并进行实验，比方说把它们的心脏放置在身体的正确一侧。我们对这一结论感到非常兴奋，因为它表明胚胎的这些物质特性可以在帮助正常发育方面发挥微妙的作用。

所以这种流体-固体的转换对于不对称的布局中很重要吗?

尽管我们外表上看起来都是对称的，但实际上内部却相当不对称：心脏在一边，肝脏在另一边，等等。在所有的脊椎动物中，这都是由一个在早期胚胎中形成的不对称的纤毛器官驱动的。在这个器官里，一堆纤毛黏在充满水的腔中。纤毛在某个特定的方向上跳动，并在内部建立流体流动，通过读取流体流动产生左右模式。这个充满水的器官内部的流动方向，可以指导整个身体如何正确模式化。这就是为什么有纤毛功能障碍的人会有反对称性，也就是说他们身体的不同部位，会出现错位对称。

现在，我真正感兴趣的是细胞形状，因为它似乎支配着这些融合组织中的许多物理特性。细胞形状在这个破坏对称性的器官中起着重要作用。在斑马鱼的胚胎中，有一组程序化的形状变化可能受到流体-固体转变的控制，这些变化碰巧产生了左右对称破坏。例如，器官顶部的细胞需要瘦长的形状，而那些在底部的细胞需要矮胖的形状。这样，更多的纤毛就会到达顶端，在那里它们可以创造出非常强的流动。



来自：

http://www.modelorg.com/models-service/animal/zebrafish.html；http://www.bio1000.com/zt/focus/banmayu.html

除了不对称发育，你还在研究如何让发育组织建立并保持清晰明确的边界。为什么这很重要?

在生物学中有很多情况下，你想要有一个清晰的边界，而边界的宽度比细胞直径要细得多。这不是歪曲的。一个清晰的边界可以确保你不会将两种类型的细胞混合，这对于胚胎发育过程中组织的分离是至关重要的，因为细胞必须分离并分隔成肠道和肝脏等。

如果你仔细观察两种流体的混合物，它们的边界会非常清晰，就像水里的油滴，它们混合在一起的范围很大，因为分子很小。但是组成组织的物体是细胞，它们的大小与器官的大小有关。这意味着这些边界必须更加清晰。如果它们不是那么清晰，如果它们像在两种流体之间的典型边界那样混合在一起，这就会导致非常复杂的结果。所以，如果你在显微镜下观察到细胞间的边界时，它们是非常清晰的。

“事实上，器官通过一种更像流体或更像固体的物质，实际上可以帮助器官正常形成并发挥作用。”

是什么使它们如此清晰?

通常，边界的清晰程度和它表面的张力有直接的关系。但人们已经测量了两种类型细胞之间的表面张力，压缩细胞群的难度有多大，当然这些数字并不大。边界的数量级太过清晰。为什么表面张力的机械测量和边界清晰度上存在这么大的差异?我们发现，这与细胞类型的融合有关。事实上，细胞之间没有空间，它们的形状取决于它们的粘附性或“粘性”程度。

在这样的系统中，相互作用并不取决于密度或邻居的距离，而是取决于你的邻居是谁以及你有多少邻居。这叫做拓扑相互作用。博士后Daniel Sussman和我决定对这个系统建模，和雪城大学的其他教员一起，一同发现这些难以置信的清晰的界面是具有拓扑作用的系统一个特殊的功能。这真的是令人兴奋，完全出乎意料。此外，请记住我们使用的顶点模型并不仅仅适用于生物细胞。如果在某种人工结构中你想要一个非常清晰的边界，比如泡沫或自组织液滴系统，你可以设计具有这种拓扑相互作用的材料。

假若这些清晰界面对维持组织的完整性很重要，那么我们能否看到它们在疾病中会分解?

这是我们工作假设的一部分。我们想知道:是什么阻止癌细胞转移？标准的做法是，它们被一种叫做基底膜的物理屏障所阻碍，后者能够将中空组织的内层与底层的层分开。但是在许多癌症（特定类型的癌症）中，我们发现细胞可以突破基底膜，但是它们不会离开肿瘤。一些研究小组已经提出，在这些清晰而柔软的边界中起作用的肿瘤的表面张力，可能在决定这些癌细胞是否能转移方面起着重要作用。癌症肿瘤如何经历流体-固体相互转化中也可能发挥着作用。

我们最酷的一项预测，是通过简单观察细胞的形状，确定组织行为是流体还是固体，以及这些细胞是否能转移。我们的顶点模型预测，在固体中，一个细胞的周长除以它的面积的平方根恰好是3.81，而随着这一数字从3.81增加，组织内的流体也会越多。这对生物学来说确实是一个非常疯狂的强预测！

在2015年，我们与哈佛大学公共卫生学院的Jeff Fredberg的团队共同发表了一篇论文，证明了这是完全正确的。从那时起，我的生物学同事就更愿意听我的。（笑）

在过去的一年里，我们的很多工作都是为了理解这一理论成立的深层原因。它指向一个基本的几何极小曲面问题。考虑下面的数学问题：你必须用一定数量的图块来平铺空间，并且每个块都必须有相同的面积。所有这些物体的最小周长会是多少？我们在二维和三维中都有证据证明（因为在三维中存在类似的问题）存在一个最小曲面。在二维空间中，最小周面积比为3.81。这意味着它是非常通用的：我们在模型使用了一个特殊的能量函数来理解刚性，这意味着任何一个能量函数都可以使周长-面积比最小化。这就是为什么它很酷。

在临床上，由于我们的研究表明细胞形状非常重要，我们希望分析胚胎或癌症患者的细胞形状，以便有一天能够用于疾病诊断。

“胚胎的物质特性，在其正常发育中起着很好的调节作用。”

我们讨论了很多关于机械力如何促进细胞发育、结构和疾病的问题。那么遗传学呢？

没错。发育生物学家也在试图理解被称为形态因子的信号分子基因和梯度是如何产生身体结构的。很明显，它们非常重要。我们的方法是互补的。它推动了关于细胞如何控制器官形成的新假设，通过证明它不仅仅是生化反馈也是机械反馈，组织本身的材料特性可能是一种非常强大的机制，可以在胚胎中产生模式，这些属性可以成为治疗的目标。

你是否一直致力于把你的机械方法和遗传方法结合起来?

老实说，当我10年前开始做这个的时候，我认为我可以在一些书中查到组织的结构，然后在上面建立生化信号网络。但现在，我认为我们才刚刚开始理解什么是力学，这足以将它与模型中的信号联系起来。

这就是为什么我对一种叫做“光遗传学工具”的新实验工具特别感兴趣，这种工具通过在细胞闪烁光来改变蛋白质或信号分子的活化。你可以用这种方式在局部处理信号分子的机制和表达，来观察两者如何相互作用，从而在发育中的组织中产生模式。还有那么多有趣的问题等待我们去研究。

翻译：非线性

审校：雪曼

编辑：李沛欣

原文地址：https://www.quantamagazine.org/the-physics-of-glass-opens-a-window-into-biology-20180611/