
现实世界中的大量问题都可以抽象成图模型(Graph Model),也就是节点和连边的集合。从知识图谱到概率图模型,从蛋白质相互作用网络到社交网络,从基本的逻辑线路到巨大的Internet,图与网络无处不在。然而传统的机器学习方法很难处理图网络信息,这种缺陷大大限制了深度学习的应用领域。于是人们提出了图网络(Graph Network),一种基于图结构的广义人工神经网络,它可以直接对真实问题进行建模,又可以利用自动微分技术进行学习,甚至有望将多个传统人工智能领域进行融合。
本次AI&Society活动邀请了北京师范大学教授、集智俱乐部创始人张江及彩云科技首席科学家肖达对图网络的原理、应用领域,以及图网络近期两个火热的子领域
——关系推理和自注意力进行了分享。

本文是对张江老师和肖达老师演讲的回顾,扫描海报中的二维码即可观看录播。PC端也可以输入网站链接进行观看:
。

深度学习中,什么是最重要的?
我们知道,深度学习已经在很多领域都有成功的应用,比如图像,语音等,那么在深度学习中最本质的因素是什么呢?
实际上,我们可以这样理解:在以前,人类的知识被我们通过编程写成程序,处理问题。而现在,我们将人类的知识编码到神经网络中,它们变成了隐藏于网络结构、节点和大量数据中的信息。
从更深层次来看,我们可以将神经网络认为是一种可微分的编程,例如深度神经网络可以用背后的计算图机制作为支撑,进行反向传播。实际上,我们将符号计算与数值计算在神经网络优化过程中进行了融合。所以我们可以进行求导,求微分的操作。那么这就意味着,深度学习可以被应用于任何可微分的领域,甚至我们可以畅想:在未来,所有的可微分的事物都是可学习的。

深度学习是怎么“玩”起来的?
让我们来回顾深度学习的运转过程:人类设置一个架构,为机器设置一个评价标准,接下来就可以让神经网络自动去学习,完成这个优化目标。
例如,图像中具有大量的平移和旋转不变性,而人类设置了卷积神经网络这种可提取多层次信息的架构,很好地将图像中的深层次信息学出来。对时间序列,我们也可以设计RNN的架构(及其变体)来学习到时间序列中的隐藏信息。当然,我们还有类似于Attention机制等更先进的架构去关注数据中的关联关系,又或者Deepmind推出的“可微分计算机”——它与冯诺伊曼的计算机体系完全不同,这可以让我们去学习整个冯诺伊曼的计算机体系。
图网络
当我们放眼大千世界事,我们会发现图像、语音、语言数据很规则,很方便处理,但很少。更多的情况下,我们有大量的非欧式的图网络数据,例如社交网络、脑影响网络等。能否对图网络进行处理呢?答案是显然的。
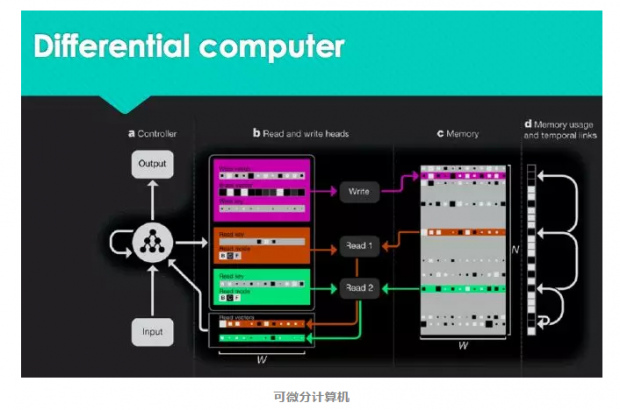
在这篇最近非常火热的综述文章:relational inductive biases, deep learning, and graph networks 中,已经提到了一种框架将深度学习与贝叶斯网络进行了融合,其结果是产生了一种具有推理能力的概率图模型。但不仅如此,他们还提出了更多思路去结合深度学习与图网络,指明了在图网络领域应用深度学习的清晰方向。
在图网络中,有很多例子可以完成对现实世界的抽象。什么是图网络呢?本质上,它是对神经网络的扩充,我们知道,神经网络的结构很特殊,而他的学习方式也通过反向传播进行连边上的权重调整。而图网络则可以从多个角度对神经网络进行扩充,具体而言,任何一个图网络都包含节点、连边、全局信息这样三个大的信息单元,每个单元都可以被表征为一个向量。相比于深度学习只能更新权重,图网络的学习发生于每一个环节上,包括对连边状态的更新、节点状态的更新和全局信息的更新。在做完前馈运算之后,它也会进行反向传播学习,因为它的每一步计算都是可微分的。
我们可以这样理解图网络的学习能力:图网络将前馈的思路放在了每一个环节,连边、节点、全局信息就都可以在反馈过程中被调整,这就使得网络的整体架构变得可学习。
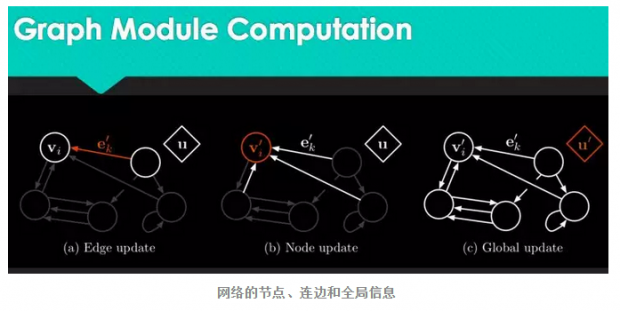
前文论文中提到的所谓的inductive bias,指的是人类对世界的先验知识,对应在网络中就是网络结构。图网络中的网络结构是固定不变的,我们可以将其理解为工程师放进去的一种先验的“偏见”,如果工程师认为A事件导致B事件发生,那么他就会在A、B之间放上一条连边,这就体现了A、B之间的因果关系,我们称之为推理能力。
图网络可以做什么?
例如我们将机械狗作为一个物理上的多体框架放在图网络上进行处理,首先,图网络可以将机械狗的每个机械结构作为一个实体,机械结构之间由关节相连,关节就可以被看做连边,而节点和连边之上都是带有信息的,这样我们就获得了一份图网络数据。每个节点上都可以有一组向量,而机械狗的运动就可以由所有的节点向量和连边向量来表示。当然,我们也可以加入更多的全局信息,例如从宏观状态上观察到的机械狗的运动信息等等。
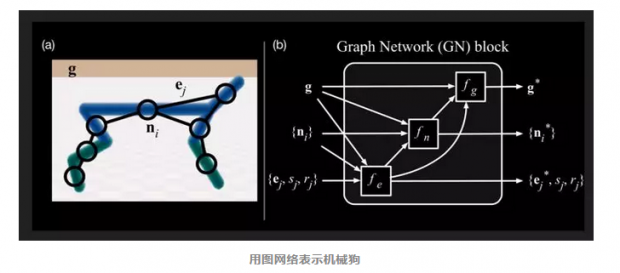
因此,我们对机械狗从各个角度进行了可微分描述,也建立了表示这些信息的图网络,接下来我们就可以学习机械狗的运动模式了。
怎样进行更高层的信息整合呢?在基本的图网络构建完成之后,我们可以在高层次对信息进行处理来完成更复杂的任务。例如,我们可以将多个图网络叠加在一起(每一个图网络都是同构的,但它们表征的信息并不同),这样我们就可以构建出多层的图网络,从而拟合复杂的运算过程。我们也可以将不同时间的图网络状态放入RNN架构中,从而完成对网络状态的预测,甚至我们可以将网络的输出作为自己的输入,进行后续状态的预测和生成。
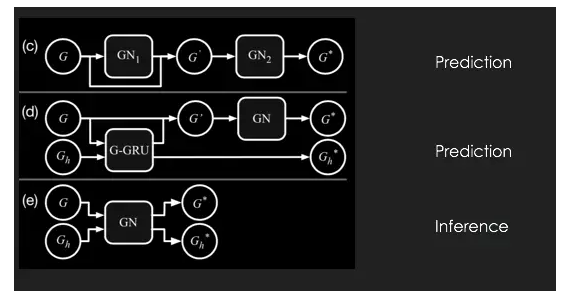
图网络的高层信息整合
除了物理系统,我们也完全可以将这一套原理放在更宏观的架构之下,例如,我们可以用这一种框架去学习网络上的动力学过程,例如在社交网络上,每个人都是节点,而人们在社交网络上的观点是怎样传播的?在交通流中,交通信息(堵车程度,车速信息等)又该怎样传播?这一类问题都可以通过图网络来解决。
图卷积
为了能够更好的整合图网络信息,我们可以对图网络进行卷积操作,具体来说,我们可以应用图信号处理领域知识,对图数据进行傅立叶变换,将卷积的定义扩展到图数据上。最终,我们可以通过图网络上的简单矩阵相乘和线性映射来表示图卷积,从而对每一组向量的信息进行深层次提取。
对图网络进行卷积之后,我们很意外的发现,图网络竟然在完全随机化的初始条件下,完成了在表征空间下的标签聚类。实际上,这正是因为图卷积操作就是在捕获图网络上的邻域信息,而邻域信息也被包含于节点和连边的数值中。在经过非线性映射之后,我们可以将其理解为对各种特征进行强化和分散处理,使特征更为明显,从而更好地完成聚类。
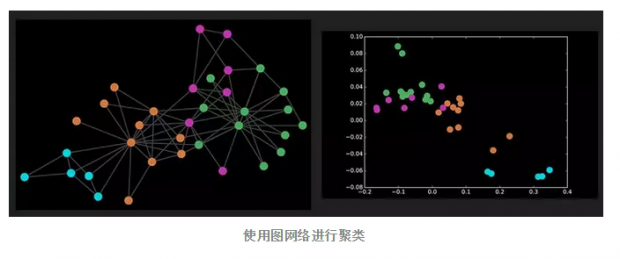
除此之外,我们还可以通过半监督学习来预测节点信息:通过已知节点的信息和图卷积方法运行图网络,标签信息就会在图数据上扩散,然后我们再用已知节点作为监督信息去调节,这就让整个网络上都拥有了标签信息,其准确度是非常高的,有些甚至可以超过80%。
此外,我们自己的研究组还做了网络上的SIR模型(传染病模型),这个模型的运作规律是:每个人有健康、染病和恢复三个状态,在每个时间步中,每个人都有一定的概率被他的邻居感染,被感染者也有一定的概率恢复健康。
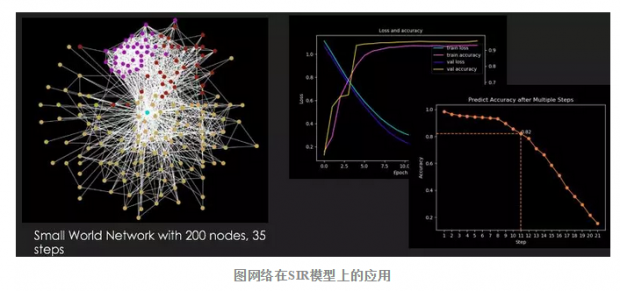
在SIR的过程中,我们可以使用图网络进行学习,用当前时刻的状态去预测下一时刻的状态,其预测效果是非常好的。更有意思的是,我们可以用已知节点的信息去预测未知节点的信息,在网络结构状态已知,部分节点状态未知的情况下,所有的节点信息都可以被比较准确地恢复。
图网络上的注意力
除了卷积之外,图网络上的注意力也是一个有趣的研究方向,我们知道注意力机制现在已经被应用于图像、语言信息的处理中,现在注意力机制也被应用于图网络数据的处理中来。
在图卷积网络中,我们可以将注意力结构内嵌其中,在每次更新节点信息时,我们需要计算出网络的注意力、注意力表示节点和节点之间的关系权重,我们可以将其理解为每个节点在进行更新的过程中更应该关注谁,谁对这个节点来说更重要。
使用图网络进行融合推理
我们知道,贝叶斯网本身表示了随机变量间的因果关系。通常情况下,贝叶斯网络的图结构需要被人为建立,并且给出节点和连边的概率分布。在深度学习出现之前,我们用隐马尔可夫过程去完成语音的学习,我们会使用到信念传播算法。但现在我们可以从新的角度去学习:将节点和连边映射为图网络,在图网络上进一步学习节点和连边的关系的运算。
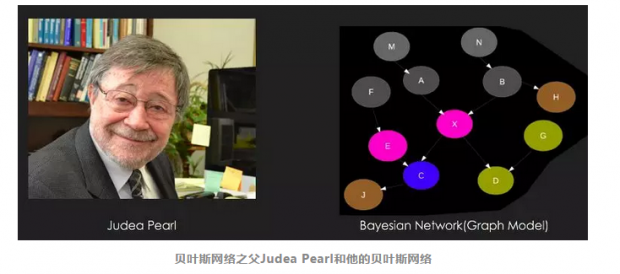
如果图结构以及他们每个节点和连边上的概率分布都是可学习的,那么只要有部分节点的数据观测信息,我们就可以推测出整个网络的观测信息,而且这是很有可能做到的。仔细看来,这个过程很有可能蕴藏着远比其看起来更深刻的意义:
具体而言,现在的技术可以做到对不可微分领域的学习,这与传统的深度学习非常不同,我们不需要结构是可微分的,这就大大拓展了深度学习的可应用范围。怎样连接不可微的部分呢?我们可以通过Policy Gradient算法完成这样的连接。例如,我们有一个复杂的神经网络,在最后一步我们需要按照概率做一个选择,而概率选择会将梯度信息的中断。而Policy Gradient则可以通过概率期望替代评价函数,并非每次都获得回报,而是通过多次采样的期望收益进行反向传播。这就使得离散的选择变成了可传递梯度的架构。
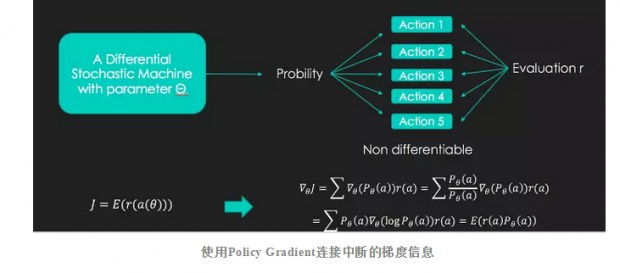
Policy Gradient模型也是有一些弱点的:他们很难优化和收敛。除Policy Gradient之外,最近也有一种新兴技术:Gumbel Softmax,他们会在选择的过程中加入Gumbel分布的随机数,导致可以获得梯度不断的概率分布信息,最终的梯度就可以被反向传播回来。这就使得我们可以在经典的Softmax操作上加入Gumbel随机数,并通过参数调节,使得梯度并不中断,从而连接中断的微分操作。
总之,现在的深度学习领域也可以被扩大到任何数据结构上,而且在更多的结构上,人们都已经有方法去解决可微分、可传递梯度的问题,此外,我们还可以看到,现在的图网络应用已经扩展到各种领域,很多原本各自平行发展的架构,现在都已经可以通过图网络进行融合,人们将原来的先验信息和图网络深度学习方法进行融合,这使得“任何事物都是可学习的”变成了可能。

什么是关系推理问题:
我们可以通过几个例子直接感受关系推理是什么:
在1917年,认知心理学家做了一个实验,给一只母鸡两个颜色纸(浅色和深色),其中浅色放上稻谷,深色不放稻谷,经过训练,母鸡可以正确的选择浅色的纸。接下来,我们将深色的纸变为白色。这时母鸡竟然会选择白色,而不是有稻谷的浅色。
其中的一种解释是,母鸡会学了纸的颜色与是否有稻谷的抽象关系:浅色有稻谷,而深色没有稻谷,白色是最浅的颜色,所以母鸡会选择白色:

在人类的例子中,我们可以进行更复杂的推理。例如Bob比Tom高,Tom比Peter高,那么我们可以自然地计算出,Tom比Peter高。这个推理虽然并不复杂,但需要人类理解其中的抽象关系,才能够正确地完成推理过程(实际上,通常只有三四岁以上的小朋友才会逐步具备这种能力):
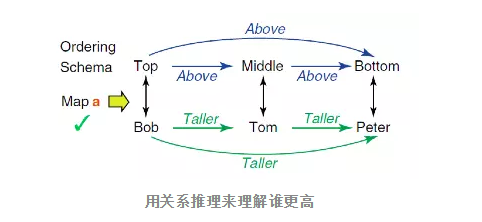
在语言学习的领域,研究发现孩子在学习语言的时候,具体的实体将会最早地被学习到(例如苹果,桌椅),而关系(例如叔叔)则会被稍晚学习到,而更复杂的if、otherwise等关系则要等到八岁才能够被正确地学习和应用。
在科学发现中,很多科研成果也是通过类似的类比推理的方法获得而来。卢瑟福认为原子和电子有吸引和旋转的关系——就像星星和太阳一样,他将太阳和星星的关系映射到原子核和原子上,这种映射我们称之为保结构映射。更具体来看,太阳和星星之间有这吸引关系,这种关系的推理也被映射到原子和电子中去——这意味着我们不但映射了位置关系,还映射了关于关系的关系(引力关系解释了位置关系)。
自然语言处理中的关系推理
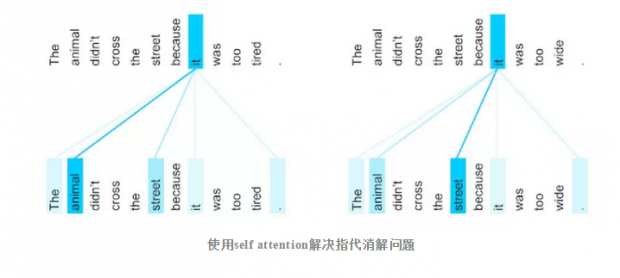
在自然语言理解中,指代消解是一个很有趣的挑战,也是最能体现关系推理能力的场景之一,如图,其中的it到底指的是什么?这对于人类来说不难回答,但现有的深度学习结构并不能很好地处理其中的问题:

而在关系推理的难题:智力测验中,我们会需要完成大量的规律、关系的探索和发现,如图:
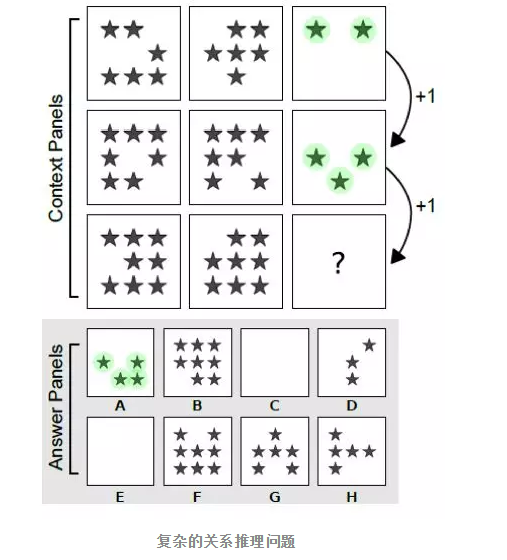
这个问题的做法是:从纵向来看,每一个方框都要比上一个方框中的五角星多一个,所以答案是A,可以看到,这个过程需要大量的关系推理,即使是人类完成这个问题也并不容易。
当前,我们已经通过深度学习在图像、语音等领域取得了很好的成就,但符号推理领域还尚未被攻克。在这两个领域之间很可能就是关系推理,到现在为止,人们对关系推理的尝试还没有取得具有大量突破性的进展。而今天分享的图网络算法是很有可能帮助我们在这个领域取得一些突破。
Memory & Attention
在翻译领域中,传统的编码-解码模型会用LSTM对句子进行编码和翻译。加入了Attention机制之后,每次生成一个目标语言的单词的时候,Attention机制都会关注到原文中的哪个位置更为重要,这就是Attention机制的原理。所以,我们也可以将Attention机制看做从Memory中的读操作。
通过Attention机制,我们可以解决很多实际问题,例如在描述大量实体状态的复杂问答过程中,我们可以通过Attention机制去关注到一个问题的多个对应答案,经过多次运算(也可以被称之为多步推理)之后,就可以将每一步需要关注的东西学到,从而找到最关键的答案。
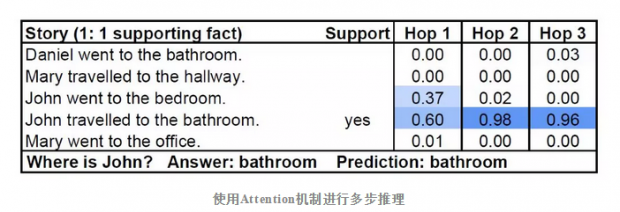
在上图中:Attention机制在不同的循环步数中关注到了John的动作和位置信息,从而给出了正确答案。
Relation Network
什么是Relation Network呢,在传统的网络中,我们可以直接通过全连接网络对输入进行映射并输出。当然,我们也可以加上一些先验知识,对每个实体单独进行映射,然后在进行全连接的运算。更进一步,如果我们认为实体之间两两是有关系的,那么我们可以将实体的两两之间组成一个联结对,然后再分别进行映射,这个映射过程就是在检验实体之间的关系是否存在,并试图量化实体之间的关系。
具体而言,Relation Network可以被应用于很多地方,例如用图片回答问题:
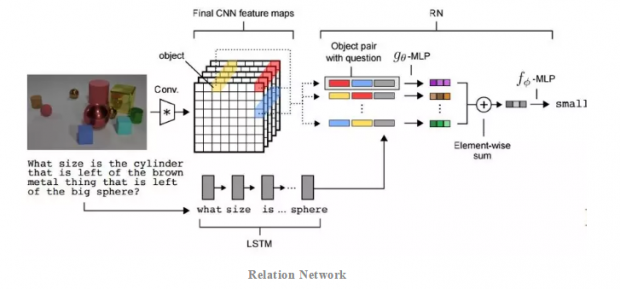
在这个问题中,我们可以让Relation Network去将任意两个Object两两组合,形成联结对,再与问题的编码相结合,通过线性映射形成对问题和答案的表示,最终再映射为对问题的解答。选择问题答案的时候,我们同样可以将每个答案和问题去拼接,通过是否有关的映射之后再映射为最终答案。
回到前文中的智商测验的问题上,如果我们把智商检测问题交给机器处理,我们发现如果用CNN或者ResNet去处理的话,其效果并不如使用Relation Network进行处理达到的效果更优。Relation Network的处理该问题的核心原理是:把每个图片作为一个实体,将图片和备选答案也作为实体与剩下的给定图片进行组合,则可以一个比较大的概率发现其中的隐藏关系。
总体而言,一般的图网络的结构具有连边的更新、节点的更新和全局状态的更新这三步。在relation network中,我们对问题进行了化简:节点更新被丢弃,我们将直接进行连边更新和全局更新,其优点是结构相对简单,尤其是可以被模块化和插装。(如果将模块加入到CNN网络中,CNN网络也就可以拥有推理能力)但他也有一个缺点:由于任意实体之间都要建立联结对,所以其计算复杂度是很高的。
Self-Attention
self attention最早被应用于翻译领域,我们可以将其理解为类似于卷积的一种结构。对于卷积来说,我们会首先定义窗口大小,然后对窗口内的向量进行卷积操作。而self attention可以将这个过程变为动态的,我们可以认为她可以从任何位置抓取信息用于运算,而具体抓取信息的位置就是Attention 机制学习得到的。
因此,Self attention可以突破窗口大小的限制,完成很多长程连接上的信息提取,例如可以用self attention解决前文提到的指代消解问题:在self attention结构进行运算时,我们可以看到it在不同的语境下,关注到了不同的实体。
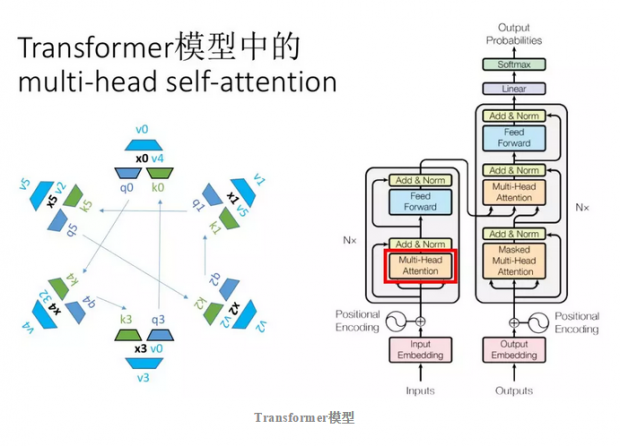
Transformer模型
Transformer模型是一个内嵌了self attention模型的网络架构,其目的是做出可以解决大量语言中的问题的通用模型。Transformer是怎样运作的呢?
假设一句话中有六个词,分别被称为X0,X1...X5。self attention需要在这六个词语之间建立联系,首先,每个词语将通过线性映射被映射为一个我们称为key 和value的向量,每一个query需要和其他key进行向量点积,其点积结果就可以被看作相关度,最终我们可以得到每个词语和其他哪个词语更为相关。
在词语的相关度被建立之后,我们就可以基于相关关系去做信息传播了,多次重复这个过程,我们就可以对节点上的信息进行更新。值得一提的,是在self attention的结构中,我们默认是没有位置信息的,因此我们常常需要在处理时间序列时手动加入一些位置信息。
在翻译模型中,我们会在输入端和输出端多次进行前文的操作,即可获得更好的词语之间的关系结果,从而达到更好的翻译效果。
在RNN中,每个词都是按顺序输入的,因此任何两个节点的关系都是需要n步运算,在CNN中,由于多层的信息处理是树状结构,因此两个节点的距离是log(n)。而在self attention中,由于任何两个词语之间都有联系,所以它们建立关系只需要一步,在长文本序列中,长程连接上的信息经过越多步传播就越容易丢失,所以Transformer模型中的self attention架构可以对关系,尤其是长程关系进行更好的提取。
通过对基于self attention模型的Transformer模型的预训练,人们可以根据少量的迁移就能在不同的语言任务(阅读理解,翻译,情感计算等)中都取得很大的进展。
总体而言,传统的注意力机制建立的关系是1对1的,而Relation Network建立的关系是多对多的关系,self attention建立的关系则是1对k的:这意味着每个节点(词语)可以对应k个关系,k是可学习的参数。self attention的一个基本的模式是:建立全局关联,交换信息,局部整合,建立新的全局关联……循环往复这个过程,self attention架构将逐步准确的找到节点之间的关系信息,而无序关注节点的空间距离。
0
推荐



 京公网安备 11010502034662号
京公网安备 11010502034662号 