编译：集智俱乐部翻译组

来源：https://www.quantamagazine.org

原题：Evolutionary Math and Just-So Stories

达尔文雀族（Darwin' finches）的故事广为人知：查尔斯·达尔文发现了多种鸟类，它们在许多表面特征上存在显著差异，每种鸟都适应加拉帕戈斯群岛的特定岛屿。根据这些鸟类的基本解剖学相似性，达尔文确定它们都是近亲，并且可能来自同一个祖先物种。目前公认的是，在孤立群岛的岛屿上，物种进化将大大加速。在某种程度上，这是因为这些岛屿的小尺寸以及它们为不断变化的物种造成的隔离。

加拉帕格斯群岛上的达尔文雀族

在最近的一篇文章“Mathematics Shows How to Ensure Evolution（种群结构如何影响进化）”中，John Rennie描述了由哈佛大学进化动力学实验室主任Martin Nowak和奥地利科学技术研究所计算机科学家Krishnendu Chatterjee领导的数学研究。他们的数学研究展现了特定的种群结构如何加速或减缓自然选择进程。

正如Rennie解释的那样，基于群岛的种群结构可以成为进化的加速器。

进化图理论（Evolutionary graph theory），是图论、概率论和数学生物学的交叉学科，研究拓扑结构如何影响种群进化。在进化图模型中，个体占据加权有向图的节点位置，节点间连边的权重表示替换的概率，权重对应于适应度的生物学概念。参见维基百科：

https://en.m.wikipedia.org/wiki/Evolutionary_graph_theory

想象一下，如同在一个岛上生活在一起的大量生物。 除非优势巨大，某种特定突变可能会在种群中永久丢失。 然而，如果少数个体经常迁移到它们自己的岛屿进行繁殖，那么适度有用的突变可能更有可能在此保存下来，并传播回主种群。

我们的第一个问题可直观展现这一现象。

有利突变能够固定（fixed，通过成百上千个体扩散到整个种群）下来的概率（p）是（1-1 / r），其中r是突变赋予的相对适应度。 因此，将适应度提高5％（r = 1.05）的突变在大量人群中仅有4.7％的固定机会。 相比之下，获得十倍适应度优势的突变几乎一定会固定下来（p = 0.9），而具有双重适应度优势的突变则具有均等的固定机会（p = 0.5）。 然而，即使突变仅具有5％的适应度的优势，如果种群数量很少，固定的可能性还是要大得多。 因此，在仅9个人的群体中，上述突变的固定概率上升至约13％。

现在想象一下，有一个拥有大岛的群岛，可以容纳一个含有数千个体的物种。 该群岛还包含几个微小的卫星岛或礁石，每个岛屿只能容纳9个个体。 这些岛屿上的个体在正常情况下不能离开它们的家园，但在一百年后，就会出现一股强大的风暴，足以将个体从卫星岛吹向主岛。 如果具有5％适应度优势的突变已经在其中一个小岛上实现了固定，那么突变会在大岛上实现固定需要多长时间？ （假设两次风暴之间的间隔足够长，以便突变在主岛上可以固定或消亡。）

Rennie在文章中描述到，如果种群中存在某种类型的联系，理论上可以在任何种群中实现这种“群岛范式”(archipelago paradigm)，即使生活环境并非岛屿的种群也是如此。 该研究使用简化的进化模型，如下图所示：

 

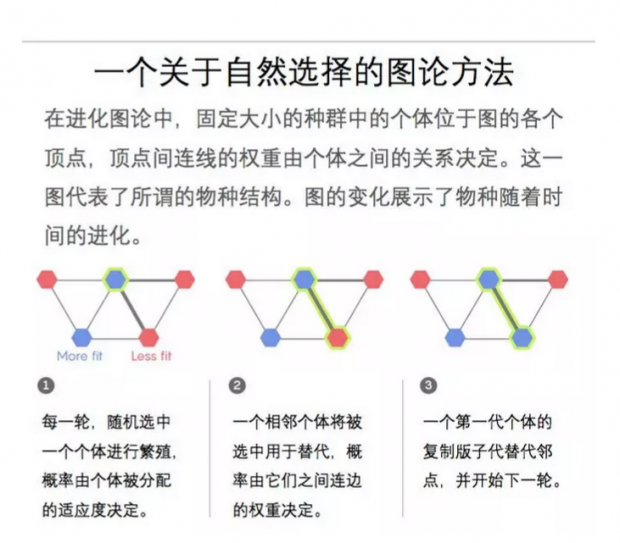
 问题二：9个个体，3种结构

 

我们的第二个问题是如何在一个由9个个体组成的简单网格中如何进行上述过程。 以下是九个个体之间可能存在的三种不同的物种结构。



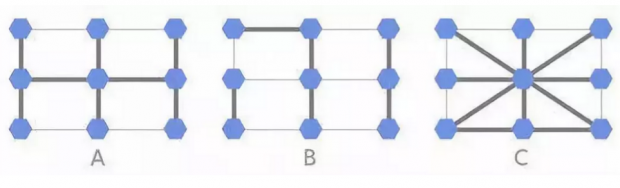
在上述的各个种群结构中，较粗的线表示强连接，较细的线表示弱连接。最初选择九个个体中的一个随机获得突变，使其适应性比其他个体高5％。在每轮中，随机选择一个个体以与其适应度成比例的概率繁殖。接下来，其中一个邻点被所选个体的后代副本替换。粗连接表示邻点被选中的概率很高，而细连接表示低概率。在这个过程中，正常个体可以被变异的个体替换，反之亦然。

这个过程一直持续到突变消失或所有9个个体都发生突变（固定）。对于三种人口结构A，B和C中的每一种，你能否预测固定是会变得更容易，非常普遍还是不那么容易发生？为什么？如果交换配置中的粗线和细线会发生什么？

喜欢编程的读者可以进行模拟，看看是否符合我们的直观期望。 假设与所选个体的连接较强的邻点的替换概率是具有弱连接的邻点的五倍。 回想一下，在9个个体中具有5％适应度优势的突变的固定概率约为13％。 任何配置的值是显著的比其大还是比其小？

这种数学推理与现实世界进化的结论有多强的相关性？ 毕竟，在这个模型中有几个假设过于简单化，甚至完全不切实际。 繁殖不会如手术般消除和替换与繁殖个体相关的某种特定动物。 

相反，每一繁殖行为都使用了种群可用的一些有限资源，从而对其所有成员施加了增量压力，最终可能影响最弱或最不健康的成员。 繁殖和替换在整个种群中并行发生，而不是连续地或局部地。 此外，如同作者所承认的，该模型仅适用于无性繁殖：有性繁殖使事情变得更加复杂。

著名的美国古生物学家和科普作家Stephen Jay Gould发出了严厉的警告，反对显而易见但没有事实证明的关于特征演变的解释，贬义地称它们为“just-so stories”，这是Rudyard Kipling的儿童故事书的标题，这些故事有着奇特的说法，例如“骆驼的驼峰是怎么来的”。这些警告已被几位作者大量应用于进化心理学以及当前“有优势的”特征起源的问题，有时带有讽刺性的幽默。

问题在于，我们很容易创建进化理论并调整数学模型的参数，以使得它们可以用来合理地论证或解释某个结论——或者与其相反的结论。 以下陈述就是一个很好的例子：“如果男性更喜欢年长的女性，那么这可以解释为：男性会把年长女性当成母亲。

数学模型当然可以提供关于进化的深刻见解。 在之前的Insights谜题中，我们已经触及了一些像这样做的著名谜题，例如Ronald Fisher断言微小突变有50％的可能性是有益的，更不用说Hardy-Weinberg均衡了。 另一个非常成功且现在被广泛接受的数学模型是Motoo Kimura的中性分子进化理论。 

但要记住的是，虽然定性定性和数学证明相对容易构建，并且可以证明某些事物在本质上可能发生，但进化生物学本质上是一种历史科学，其关键问题是：它是否真的以我们描述的方式发生？

这个论断很难证明。证明进化论（无论是用数学的还是用其他的方式）需要像达尔文本人所做那样进行艰苦的实地工作。 最近一个特别的野外生物学的例子是Rosemary and Peter Grant夫妇的团队，他们每年在加拉帕戈斯群岛的一个小岛上度过几个月，持续了40多年，勤奋地标记了超过20,000只鸟，以便观察达尔文雀的行为。

刚刚提醒你不要相信进化论的那些故事，接下来让我告诉你另一个有趣的例子：它被称为祖母假设（grandmother hypothesis），意思是从进化的角度看，祖辈会帮助人类、鲸鱼等各种动物活得更久。假设是，通过为后代的孩子们收集食物，年长的女性可以让女儿们更快地生育更多的孩子。因此，最长寿的祖母有最多的孙辈，她们传递了长寿的基因。

在某一个时间节点上，用于照顾体弱多病的祖父母的家庭资源消耗，超过祖父母帮助养育新后代的好处。这个时间节点被不断推迟，并且从消极的关联变成了积极的关联。但是，即使在现代，图论模型中描述的替换选择仍然存在且良好。

Jacob Bronowski以图形方式描述了现代游牧民族的关键时刻会发生什么：“当他们无法越过最后一条河时，老人会怎么样？别无选择，他们留下来等待死亡。只有狗才会因为看到一个人被遗弃而感到困惑。人们接受游牧习俗，他已经走完了他的旅程，最后没有其他地方可去。”

上文讨论的图论模型可以应用到人类身上的真实场景：在个体（祖母）身上的选择性优势，同时也会让强联系个体（比如孙辈）相对于别人（无血缘关系）处于劣势。

这个假设可能是真的吗？对化石牙齿进行的衰老研究提供了一些经验性的证据，这些研究表明大约3万年前，鲸鱼的寿命开始稳定地增长，而且在长寿的鲸鱼中也有老年雌性会帮忙把孙辈从小养到大。 

然而，数学模型比比皆是，可能在另一项研究中祖母假设对寿命几乎没有影响，但到了另一项研究中，根据祖母假设仅用六万年就可能导致物种寿命翻倍。

对此你有什么看法？

翻译：惠惠 Freya

审校：刘培源

编辑：孟婕

原文地址：

https://www.quantamagazine.org/the-evolutionary-math-puzzle-20180815/