社交网络中的幂律分布：为什么有的人微信好友5000而你只有500？-集智俱乐部的财新博客-财新网

导语

研究社交中已有的人际关系结构可以帮助你在交新朋友时建立更坚实的关系。

编译：集智俱乐部翻译组

来源：quantamagazine

原题：How network math can help you make friends

当你来到一个新的学校、开始一个新的工作、或者搬到一个新的城市时，你要如何去结交新的朋友呢？

你可以采取积极的方法，比如和受欢迎的孩子或者某些大佬们建立战略联系。或者完全凭运气，通过随机的分组和关联来建立新关系。

无论你采取什么样的方式，理解你新交际圈已有的关系结构可以帮助你建立牢固的关系，这将最终决定你的交际圈。

分析社交结构

假如你要搬到一个新的陌生的城市 Regulartown ，这里有一个奇怪的规则：每个人最多可以有四个朋友，每个人都想最大化他们的交际圈。Regulartown 的交际结构会是怎样的呢？

为了探究这个问题，我们将使用网络分析的数学方法。

网络图

简单来说，网络是一组节点相互连接的结构。网络在数学上是有多种性质：它们可以代表计算机和连接它们的线，也可以代表作者和他们的合作者，还可以代表一个魔方的状态和改变这些状态的动作——不管这些连接是真实的还是抽象的，本质上这其实就是连接的集合。

为了研究 Regulartown 的社交圈，我们将建立一个网络，网络中的节点是人和人之间的关系。

表示网络的一个简单方法就是把节点想象成一个一个的点，然后把其中的连接想象成线段，我们也称之为边。这个网络图可以让我们看到它的结构。

那么，Regulartown 的社交网络会是什么样子的呢？在某种程度上，它可能看起来像这样子：

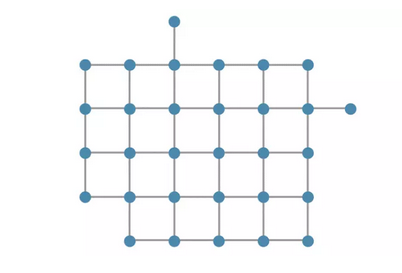
其中的每个人都会试图找到他们的四个朋友，当新的人搬到城市里的时候，他们会寻找一个不够四个朋友的人。通过这种方式，网络会随着时间的推移而继续地增长，随着新节点的加入，图的边缘会不断地拓展。（但是也有可能形成独立的小型网络，但是我们先在这个例子中忽略这种情况。）

如果网络图可以显示出一个清晰的结构的话，这是非常具有启发性的。

但是，当网络变得庞大又不存在像 Regulartown 这样规则的结构的时候，网络图可能就没那么有用了。这需要发展不同的方法来分析网络的结构。

度数分布

一种方法是考虑网络的度数分布。

在网络中，一个节点的连接数被称为节点的“度”。一个度数高的节点会与更多的其他节点相连，度数低的节点会与更少的节点相连。

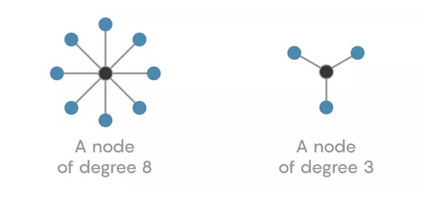
节点的度是网络的一个重要的度量，但它是有局部性的：它只能描述一个单一节点的网络结构。但是通过同时考虑所有节点的度，我们可以创建一个工具来理解某个网络的全局结构。

在我们的社交网络中，每个节点的度是每个人拥有朋友的数量。在 Regulartown 中，大多数人会有四个朋友，所以大多数节点的度数都为4。没有居民会有四个以上的朋友，但是有些人会有四个以下的朋友，于是会存在3、2或者1度的节点。

我们可以这样总结度的分布：

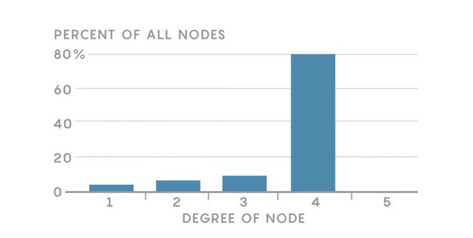
这个直方图表达了我们网络结构的重要信息。在这个简单的例子中，它可能没有告诉我们多少网络的信息，但是我们仍可以看到度的分布是如何成为理解不同类型网络的强大工具的。

接近平均：随机交友模型

如果我们来到了一个新的城镇。比如在 Randomville，人际关系是随机的。随机性可能会很麻烦，所以我们得把事情界定清楚：我们会把城镇中的每一个人想象成一个网络中的一个节点，这使得每条边都是一组人际关系。为了生成随机的人际关系，我们可以随机选择一个可能的边并将其整合进网络，然后在这两个点之间建立联系来表示建立人际关系。

那么Randomville的网络会是什么样的呢？我们假设从一堆节点开始，并随机添加一些边，于是网络图可能会是这样的：

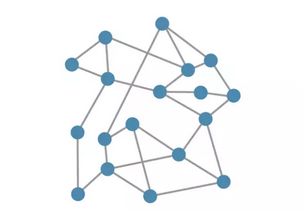
可能很难在这个图中看到结构。但是这个网络的度的分布式很有启发性的。虽然不容易直接计算，但是我们可以通过一个简单的例子来推导一些重要的属性。

想象一下，你是 Randomville 10个人中的一个。那么有多少种可能的人际关系？这10个人中的每一个人都可能与其他的九个人相连，所以你似乎可以画出10x9=90条边。

但是这实际上是可能的人际关系数量的两倍：每个人相互之间只算作一次。因此可能的人际关系的数量实际上是90除以2，即45种。

现在假设我们随机选择一个人际关系，也就是说，我们随机选择网络中45条边中可能的一条。它与你相连的可能性有多大？好吧，有九条可能的边会从你拓展到其他的九个节点。由于45条中有9条与你相连，所以随机选择的边与你相连的概率是9/45，或者说20%。

但是这个观点同样适用于Randomville中的每一个人，因此每个节点都有20%的机会会与随机选择的其他边相连。

现在，当边（和节点）被添加时，这些概率会稍微改变，但是从长远来看，它们将大致保持不变。这意味着，人际关系在 Randomville 各处的分布式相当均匀的。可能会有一些细微的变化，但是一个的朋友很多或者很少都不大可能。

在 Randomville，几乎每个人最终都可能会拥有接近平均数的朋友。

这些熟悉的特征体现在随机网络的二项式的度的分布中。

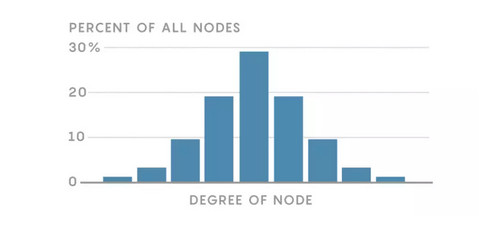
通过观察这个网络度的分布，我们可以推断出一种特殊的一致性：当涉及到连通性时，大多数节点是平均水平的，极少数是极端水平的。当涉及到理解网络结构时，这是非常有用的信息。（当有新增节点，比如有一个新人来到这个城镇，分布会稍稍改变，但是一般性的特征会维持不变。）

但是这两个例子都不是现实的人际关系模型，Regulartown 的最多四个朋友的规则和 Randomville 随机交友的模型都不是人际关系的实际模型。实际中，人们可以有四个以上的朋友，有很多朋友也并不像二项分布那样的奇怪。

那么，什么才是实际情况的人际关系模型呢？

偏好依附：实际交友模型

当你与朋友的朋友和朋友建立关系时，你们的人际关系结构很有可能会有一些其他现实世界网络的共同特征，比如食物网、蛋白质反应网络、互联网。这些特征描述了所谓的“无标度”网络，这是过去20年中主宰网络科学的一种连接模式。来自数学、物理学、经济学、生物学和社会科学的研究人员都看到不同领域无标度网络的踪迹。

一个复杂的无标度网络，表示了社交网络的元数据。

无标度网络的结构依赖于“偏好依附”这一简单原则。偏好依附是一个大者愈大的网络增长规则：一个有着更多连接的节点相比于连接更少的节点会有更大可能性获得新的连接。

这显示了新连接对度数较高节点的偏好。

这对人际关系的形成有意义吗？

一般来说，认为有更多朋友的人更有可能交到新的朋友似乎是很合理的。因为他们已经有了更大的交际圈，所以他们更有可能通过现有的关系结交到新的朋友。拥有更多朋友可以创造更多交新朋友的机会。

实际上，他们已经有了很多朋友，这表明他们可能有某种能力或者说亲和力来交更多的新朋友。这种能力可能会吸引其他人，就像流行网站上链接到其他网站和博客上的链接一样，已经建立的城市会招来新的铁路和航线规划。

虽然无标度网络的发展有很多种因素，但是许多人认为，偏好依附是最根本的因素。它对网络的度的分布有着惊人的影响。

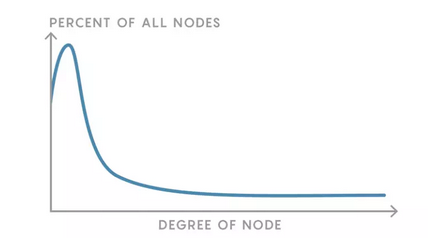
偏好依附预示着“长尾”分布。网络中的大多数节点都是低度数的节点，但是仍存在度数非常高的节点。这与 Regulartown 和 Randomville 中交际网络形成了鲜明的对标，后者节点很少或者没什么度数高的节点。

这些度数高的节点就像是中心一样，是无标度网络的一个关键的特征。

他们是交际网络的社交天王，处于经济中心的银行，区域互联网路线经过的中央路由器，表演届的 Kevin Bacons。中心的存在可以给一个庞大的网络带来一个小世界的感觉——例如，从 Facebook 上20亿人中随机选择任意的两个用户，他们的好友平均不到四个。

此外，网络中心的数量和多样性也使得网络能够抵御特定的故障，例如：即使许多互联网无法连接，但是消息仍然可以传递，一部分的原因是因为消息仍有很多方式来进出这些中心。

虽然人们似乎在无标度网络及其高级特征的效用上达成了一致，但是这一研究领域并非没有争议。这些度的分布的精确数学特征很难解释。

幂律分布

在网络科学先驱和物理学家 Albert-László Barabási 的《链接：网络新科学》（ Linked：The new science of networks ）一书中，他认为表现出偏好依附的网络，其度的分布基本上遵循幂律分布。

在许多物理场景中都可以看到幂律分布，比如引力场和电磁场的平方反比定律。他们可以表示为f(x)=a/x^k的形式，图像一般长这样：

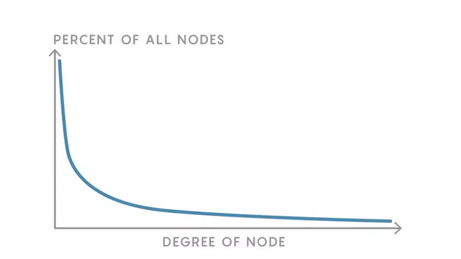
幂律分布确实有一条大尾巴。但是到底有多大呢？也就是说，在这样的一个网络中，我们期望每个中心的度应该是多少呢？

今年早些时候发表的一项研究分析了1000个现实世界的网络，得出的结论是：只有三分之一的网络拥有可以通过幂律分布来合理描述的度的分布。

题目：

Scale-free networks are rare

地址：

https://arxiv.org/abs/1801.03400

许多网络的度的分布可以用“指数”或者“自然对数”的分布来更精确地描述其度的分布。它们可能具有无标度网络的高级特征，但是如果没有预期的度的分布，它们真的可以被认为是无标度的吗？这真的重要吗？

如果我们想要把我们的理论和我们的数据联系起来，这就很重要了。偏好依附真的是无标度网络形成的主要因素吗？或者是否还有其他的因素也扮演着重要的角色，这些因素可能会把度的分布推向不同的方向吗？

回答这些问题，并找出下一步要问的正确的问题，这是充分了解网络性质和结构，以及它们如何发展和演化的一部分。

这些争论还提醒我们，数学本身就像我们的网络一样，是一系列不断演变的连接。在网络科学这一个相对年轻的领域中，当代的研究正在挑战20年前的猜想。随着新的思想加入网络科学，它们把我们所有人连接到过去和未来的数学中。

因此，当涉及到数学，就像在人际关系中一样，你最好找到数学的中心，并最大化你的度。

翻译：夏佳豪

审校：李周园

编辑：王怡蔺

原文：https://www.quantamagazine.org/how-network-math-can-help-you-make-friends-20180820/

话题：