论文解读：辛梯度优化——多人博弈纳什均衡的全新解法-集智俱乐部的财新博客-财新网

导语

论文 "The Mechanics of n-Player Differentiable Games" 荣获机器学习顶会 ICML 2018 最佳论文提名奖，它创新性地提出一种可以在普通博弈中寻找稳定不动点的算法——辛梯度调节算法（SGA），该算法与近期提出的在GANs中寻找稳定不动点的算法有同样优秀的表现，并且适用于更普遍的博弈问题并保证收敛性。

从多模型优化问题到多玩家博弈

近年来，机器学习的进展很大程度上依赖于梯度下降的使用，梯度下降使得一个目标最终可以收敛到某个局部最小值，从而优化模型参数。然而越来越多的模型需要优化多个目标，如生成对抗网络、分层强化学习、合成梯度等。

生成对抗网络：generative adversarial networks

分层强化学习：hierarchical reinforcement learning

合成梯度：synthetic gradients

思考这类问题的正确方法是——将它们解释为博弈论问题，解决这些问题就是要找到每个目标的纳什均衡而不是局部最小值。

目前在博弈中使用基于梯度的方法并没有得到很好的研究。

梯度下降等无悔算法能使博弈中的目标收敛到一个近似的相关均衡（coarse correlated equilibria）,但是其动力学计算不能收敛到纳什均衡（Nash equilibria），甚至不能稳定下来。已有的用于找到稳定不动点的算法也局限于两个玩家的博弈，还不能应用到多玩家的普通博弈中。

随着对抗性以及多目标的模型架构的发展，这方面的研究将变得越来越重要。

超越GAN的辛梯度条件算法（SGA）

在这篇论文中，作者提出了一种新的方法来理解与控制普通博弈中的动力学，其关键成果是把二阶动力学分解为两个部分。

第一部分与潜博弈（potential games）有关，它随着隐式函数梯度下降而减小；第二部分与哈密尔顿博弈（Hamiltonian games）有关，这是一类新的遵循守恒定律的博弈，和经典机械系统中的守恒定律类似。

这种分解启发作者提出了辛梯度调节算法（Symplectic Gradient Adjustment， SGA），这是一种可以在普通博弈中寻找稳定不动点的新算法。大量基础性实验表明，SGA与近期提出的在GANs中寻找稳定不动点的算法有同样优秀的表现，并且适用于更普遍的博弈问题并保证收敛性。

在GANs中寻找稳定不动点的算法包括梯度下降（gradient descent）、乐观镜像下降（optimistic mirror descent, OMD）、同时梯度下降（simultaneous gradient descent）等等，相比之下，SGA 更具竞争力，不仅能够快速找到稳定不动点，还能够应用到多玩家博弈问题。

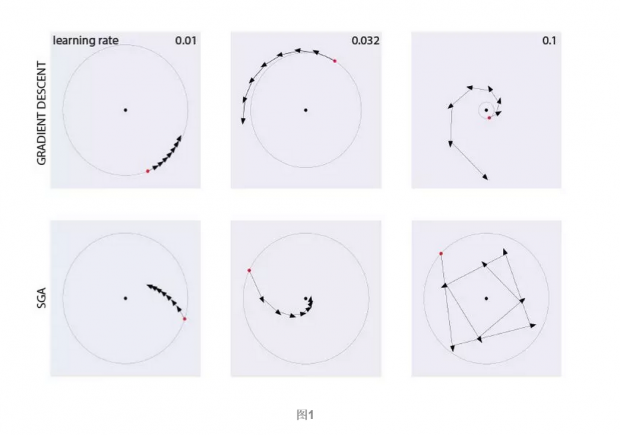
由图1可知，梯度下降对学习率的选择很敏感，学习率为0.01时缓慢收敛，学习率为0.032时缓慢发散，学习率为0.1时快速发散。相比之下，SGA能够更快、更鲁棒地收敛，只有在学习率为0.1时，起始阶段稍微偏离稳定不动点，但很快就调整过来，趋向稳定不动点收敛。

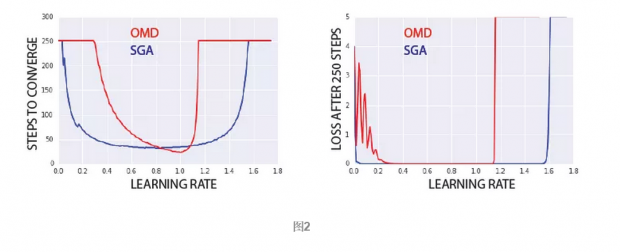
由图2可知，虽然OMD的峰值表现比SGA好，但是在大部分学习率下，SGA更快收敛。而OMD在学习率为[0.3, 1.2]之外不收敛。SGA允许我们设置更高的学习率，从而使目标更快收敛。

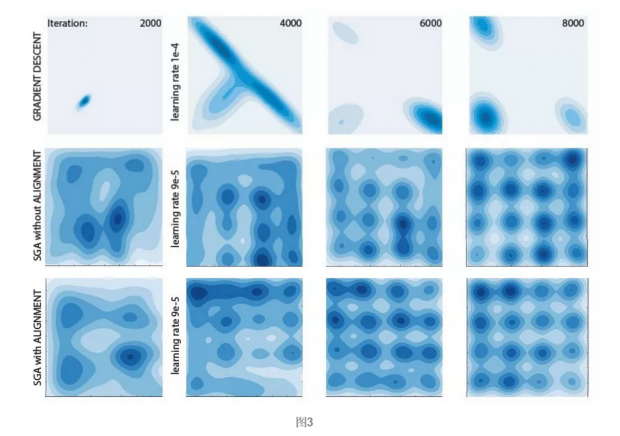
图3展示了经过2000、4000、6000、8000次迭代后的结果，可以看到，同时梯度下降会出现模式崩溃和模式跳跃，而没有进行对齐的SGA平滑收敛，有进行对齐的SGA更快收敛。可见，SGA在性能上优于同时梯度下降，并且对齐调节算法能使目标更快收敛。

如何在普通博弈中找到稳定不动点？

这篇论文提出的方法是将博弈动力学的二阶结构分解为潜博弈和哈密尔顿博弈，然后使用辛梯度调节来找到稳定不动点。

在论文中，作者首先对博弈问题进行数学定义，声明不限制参数集（例如，概率单纯形），不要求损失是凸的，玩家甚至可以通过神经网络进行交互，例如GANs。然后作者指出多玩家博弈的损失不是单一函数，若使用梯度下降，其动力学计算不能收敛到一个不动点。

作者接着讨论了著名的零和双矩阵博弈（zero-sum bimatrix game）问题，指明同时进行多个目标梯度下降的动力学可以使用哈密尔顿等式重新定义。这样做的好处是，哈密尔顿函数上的梯度下降可以收敛到纳什均衡。

双矩阵博弈：在博弈论中，双矩阵博弈是两个玩家同步进行的博弈，每个玩家持有有限个可能动作。这样博弈能够用两个矩阵（1号玩家的收益矩阵和2号玩家的收益矩阵）来描述，因此被称为双矩阵博弈。

零和博弈：零和博弈是博弈论的一个概念，属非合作博弈。指参与博弈的各方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加总和永远为"零"，双方不存在合作的可能。

纳什均衡：任何一方采取的策略都是对其余所有方采取策略组合下的最佳对策；当所有其他人都不改变策略时，为了让自己的收益最大，任何一方都不会（或者无法）改变自己的策略，这个时候的策略组合就是一个纳什均衡。在数学领域中，纳什均衡在博弈函数中就是鞍点。

然后作者对Helmholtz分解定理进行推广，推导出任何博弈的Hessian矩阵都可以分解为对称矩阵和反对称矩阵。

前者就是众所周知的潜博弈，是梯度下降收敛的博弈，已经得到深入的研究，很容易解决。后者被作者称为哈密尔顿博弈，同样很容易解决。

对于双矩阵问题，哈密尔顿博弈等价于零和博弈；对于非线性的损失或者多玩家参与的问题，哈密尔顿博弈与零和博弈有所区别。作者同时证明了哈密尔顿博弈遵循守恒定律，这使我们能够通过对守恒量进行梯度下降来解决哈密尔顿博弈。

Helmholtz分解定理：空间区域上的任意矢量场，如果它的散度、旋度和边界条件已知，则该矢量场可以表示为一个无散矢量场和一个无旋矢量场的叠加。

潜博弈：在博弈论中，如果所有参与者改变策略的激励可以使用单个全局函数来表达，则这种博弈被称为潜博弈，这个全局函数被称为潜函数。这个概念起源于Dov Monderer和Lloyd Shapley在1996年的一篇论文中（Monderer, Dov; Shapley, Lloyd (1996). "Potential Games". Games and Economic Behavior. 14: 124–143. doi:10.1006/game.1996.0044）。

哈密尔顿博弈：本文作者首次给出定义，并命名，其概念与1992 Lu等人提出的哈密尔顿游戏不同。哈密尔顿矩阵是反对称矩阵，玩家之间的所有成对相互作用都是零和的。

一般来说，哈密尔顿博弈与零和博弈相关但不同，作者在文中给出三个具体例子来帮助理解哈密顿博弈的含义：既是零和博弈又是哈密顿博弈的实例、是零和博弈但不是哈密顿博弈的实例、是哈密顿博弈但不是零和博弈的实例。在某些条件下，哈密尔顿守恒量的梯度下降法能找到纳什均衡。

作者接着证明了稳定不动点是局部纳什平衡。因此设计一种能够找到稳定不动点的算法，就能使目标的动力学计算收敛到纳什均衡。

于是作者提出辛梯度调节算法，这是一种基于梯度的方法，能够在普通博弈中找到稳定不动点。SGA满足一些基本要求，它不仅兼容原有的动力学，还能保证在潜博弈和哈密尔顿博弈中找到稳定均衡，甚至避开不稳定均衡。

对于所有博弈，正确选择调节的符号是非常重要的，因为它决定了目标在稳定均衡和不稳定均衡附近的行为。因此作者讨论了如何设置调节的符号能使得目标收敛到稳定不动点。作者还发现，对齐调节算法允许我们设置更高的学习率，从而使目标更快、更鲁棒地收敛。

应用：解决多玩家博弈问题

梯度下降能够找到局部极小值，但对于优化多个互相影响的目标来说，我们不需要找到局部极小值，而是要找到稳定不动点，因此关键是要理解和控制互相影响的损失之间的动力学。并且，提出的解决方法不仅仅是针对两个玩家的对抗性博弈问题，而是能够应用到处理多玩家问题。

广义Helmholtz分解为博弈动力学提供了强大的新视角，这种分析方式与玩家数量无关，它是损失的同时梯度与二阶项的对称和反对称矩阵之间的相互作用，能指导算法设计并控制梯度调整的动力学。

辛梯度调节算法是Helmholtz分解的直接应用，这不是找到稳定不动点的唯一或最佳方法。深入理解潜分量和哈密尔顿分量之间的相互作用有助于找到更有效的算法，特别是不使用Hessian矢量积的纯一阶方法。

论文最后提出一个哲学观点，这篇论文的目标是找到稳定不动点（例如，这种状态下的GANs能产生令人满意的样本）,而不关心博弈中玩家本身的损失。梯度调整可能导致玩家增加损失，牺牲自身利益，但这有利于收敛到稳定不动点，因此这是合理的。

作者：王佳纯

编辑：王怡蔺

论文下载：

http://proceedings.mlr.press/v80/balduzzi18a/balduzzi18a.pdf

补充材料：

http://proceedings.mlr.press/v80/balduzzi18a/balduzzi18a-supp.pdf

话题：