编译：集智俱乐部翻译组

来源：countbayesie

原题：Bayes' Theorem with Lego

 

 

关于贝叶斯定理

 

贝叶斯理论简单来说就是下面这个等式：

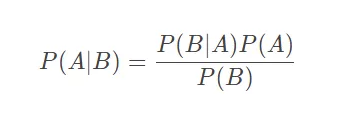
这个公式本身并没有那么可怕，它甚至都没有求和号。不过公式的背后描述的到底是个什么故事？让我们用一堆乐高积木和一些具体的问题来探索贝叶斯理论。

积木的概率空间

我们有一个面积为6*10的乐高积木拼图，我们把它假设成乐高积木的概率空间，在这个空间下有蓝色、红色、黄色的乐高积木，其中黄色的积木在红色和蓝色积木的上方，接着我们尝试着用更数学化的语言来描述这堆积木，比如从概率的角度：

在积木的底层，有60块小积木，其中蓝色40块，红色20块，用概率描述也就是积木为蓝色的概率以及积木为红色的概率，可以表示成以下公式：

重要的是，这两个概率的加和为1，也就是：

也就是说红色积木和蓝色积木可以组成整个概率空间，那么黄色积木去哪里了呢？

看上面的图片，如果我们要从这个6*10的积木拼图中随机取出一个积木，这个积木是黄色的概率为：

但是我们无法直接将P(黄色)与P(红色)、P(蓝色)的概率相加，否则你会得到一个超过1的值。实际上黄色积木的下面要么是蓝色积木要么是红色积木，而取出一个黄色积木的概率，与它处在红色概率空间还是蓝色概率空间有关，我们把这种概率叫做条件概率，用P（黄色|蓝色）表示在蓝色概率空间下取出黄色积木的概率。

 

 

通过看图算出条件概率

我们怎样才能算出这个条件概率呢？实际上如果我们要算出P(黄色|红色)，我们或许会经历几步：

1. 将红色积木和蓝色积木分开

2. 我们得到面积为2*10的红色概率空间

3. 在这个空间上，黄色积木有4块

4. 将黄色积木和红色积木分开

5. 计算出P(黄色 | 红色) = 4/20

很棒，到目前为止我们计算出了给定红色概率空间下，取出黄色积木的概率。但是，如果我们将事件和条件反过来，如何计算在取出的积木是黄色的条件下，下方积木是红色的概率，也就是如何计算P（红色|黄色）呢？

通过看这个图，你很容易能发现，一共有6块黄色积木，其中2块下面是蓝色，4块下面是红色，所以取出一个黄色积木下面是红色积木的概率就是4/6。如果你是这样思考的，那么也就恭喜你，成功地独自的探索了一遍贝叶斯定理。

 

 

通过数学计算条件概率

 

如何用数学的表达来重复我们上面的过程呢？

相比数学的语言是简单而严谨，人类的直觉在推理过程中总是跳跃的。从直觉到贝叶斯定理，我们还需要费些功夫。

第一我们先算出红色积木的数量，跟上面的计算方式相同：

    红色积木的个数 = P(红色) * 总积木的数量 = 1/3*60 = 20

第二，在我们已经知道P（黄色|红色)，也就是底层是红色积木的条件下取出黄色积木的概率时，我们可以得到：

在黄色下面的红色积木的个数 =

 P(黄色|红色) * 红色积木的个数 = 1/5*20 = 4

1. 首先我们试着用数学的语言，推出“一共有6块黄色积木”这个结论。推出这个结论，我们只需要用通过以下计算：

   黄色积木的个数  =  P(黄色) * 总积木的数量 = 1/10*60 = 6

2. 接着，如何得到“其中4块底下是红色”这个结论呢？

3. 最后计算出红色积木上是黄色积木的概率：

        P(红色|黄色) = 在黄色下面的红色积木的个数 /  黄色积木的个数 = 4/6

不过这还不太像贝叶斯公式，我们再重写梳理一遍这个过程：

P(红色|黄色)  = P(黄色|红色) * 红色积木的个数  /  P(黄色) * 总积木的数量

P(红色|黄色)  = P(黄色|红色)* P(红色) * 总积木的数量  / P(黄色) * 总积木的数量

最终我们得到：

P(红色|黄色)  = P(黄色|红色)* P(红色)  / P(黄色）

这就是贝叶斯定理！

 

 

回顾一下

 

上面的实验提到了两点：

• 概念上，贝叶斯定理是服从直觉的。（我们只是用数学语言重写了一遍我们的直觉的推理。）

• 同时，贝叶斯定理的形式化表示，不一定是显而易见的。（推出最终的公式，我们还需要多几步数学的表达）

数学的好处在于，它把我们的直觉变成了推理，这样了既保持了跟直觉的一致性，又能提供一个新的有效的工具，去解决那些比乐高积木更复杂的问题。

如果想了解更多关于，贝叶斯定理和贝叶斯推理的故事，你可以参看这些帖子：

• Learn about Bayesian Priors with Han Solo

  https://www.countbayesie.com/blog/2015/2/18/hans-solo-and-bayesian-priors

   

• Understand Bayes' Factor and Bayesian Reasoning by exploring a classic episode of the Twilight Zone

  https://www.countbayesie.com/blog/2016/3/16/bayesian-reasoning-in-the-twilight-zone

   

• Use Bayes' Theorem to reason about the probability that your friends are really allergic to gluten

  https://www.countbayesie.com/blog/2016/1/22/why-you-should-believe-your-friends-claims-about-food-allergies

翻译：文雷

编辑：王怡蔺

原文：

https://www.countbayesie.com/blog/2015/2/18/bayes-theorem-with-lego