目前,大部分相关工作都是基于静态网络的嵌入,即没有考虑到网络随时间的演化。而真实网络的连边和节点以及节点特征都是动态的。
所以,基于动态网络、在网络嵌入中考虑时序信息更加符合实际,也会使得嵌入获得更加丰富的信息。
QQ、微信中的用户以及他们的好友关系会组成一张巨大的社交网络,该网络中包含的信息在好友推荐、社群发掘和用户画像等任务中有重要作用。
而网络表征学习( NRL)或者网络嵌入(NE)是分析这类网络、挖掘其中信息的重要方法。NRL/NE的核心是将网络中的节点、连边或者社团嵌入到低维空间中,从而转化为结构化的数据,以支持下游其他任务,例如节点分类、链路预测和社区发现。
网络表征学习(Network Representation Learning, NRL)或者网络嵌入(Network Embedding, NE)是非常重要的网络分析方法。其核心在于将网络这种非结构化的数据嵌入到低维空间中,用低维向量来表征网络中的节点和连边,或者整个网络。
现实世界大多是动态网络(Dynamic Networks),其连边、节点都是随着时间不断变化的。例如社交网络中新用户的加入、新好友关系的产生,会导致网络中出现新的节点和连边。这些时序信息是动态网络的重要部分,是网络的演化机制和其上动力学的体现。
但是现有的大多数嵌入方法只能处理静态网络(Static Network),无法编码网络的时序信息。
近期,越来越多的学者注意到了这个问题,并提出了自己的动态网络嵌入方案,本文对该方法近期的论文进行简单介绍,尽量为大家呈现动态网络嵌入的最新进展。更全的列表见参考文献。
一、什么是网络嵌入
读者很有可能不清楚什么是NRL/NE,故在此做一简单介绍。
传统的机器学习大多处理的是以特征向量所表示的结构化样本,而网络(graph)是非结构化的数据。所以,要想用丰富的机器学习模型来挖掘网络中的信息,第一步就是将网络嵌入到向量空间中。
如图1所示,网络在不同尺度上被嵌入到低维向量空间(此处为2维),从而化为结构化的数据,并尽可能的保留了原有的信息。静态网络嵌入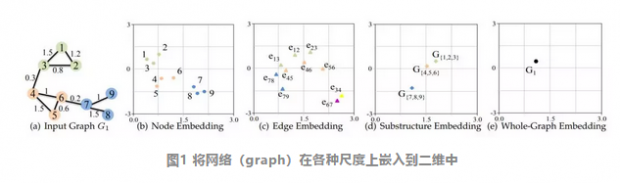
算法就是在这种不变的拓扑结构上将网络映射到低维空间。
那将静态网络嵌入算法直接用到动态网络上有什么不足呢?
1. 网络虽然变化很小,但是必须重新训练模型
2. 两次嵌入的向量不稳定,变化较大
3. 不能捕获网络演化的时序信息
4. ......
所以,要解决上述问题,提高网络的嵌入效果和效率,必须在动态网络的基础上开发嵌入模型。
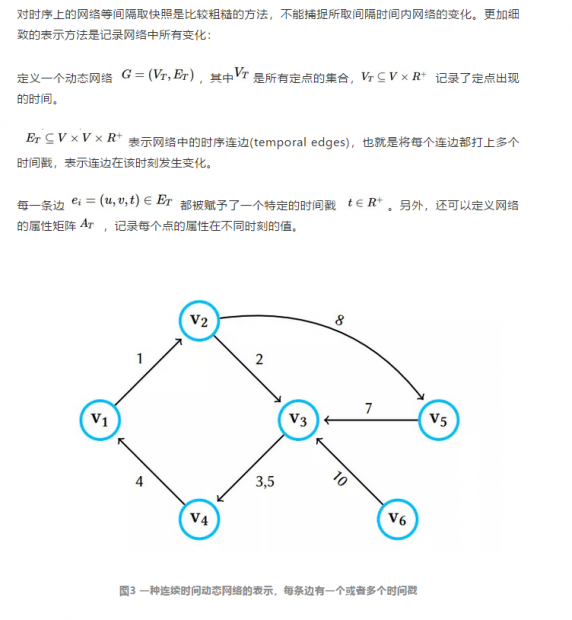
二、动态网络的表示

2.1 Snapshot
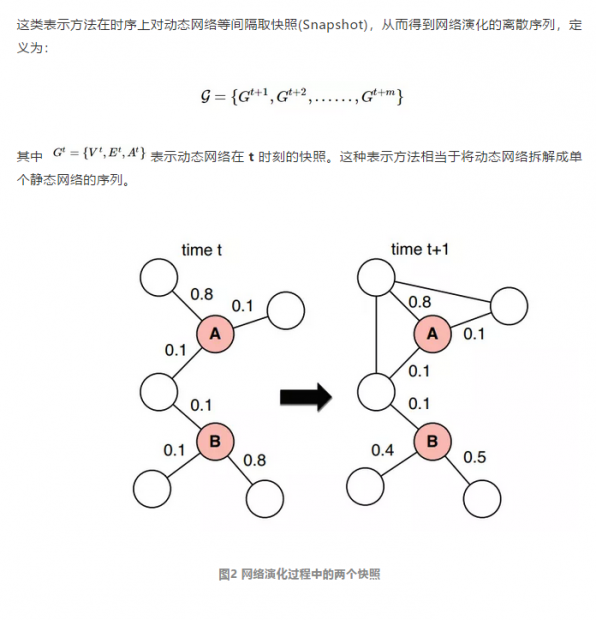
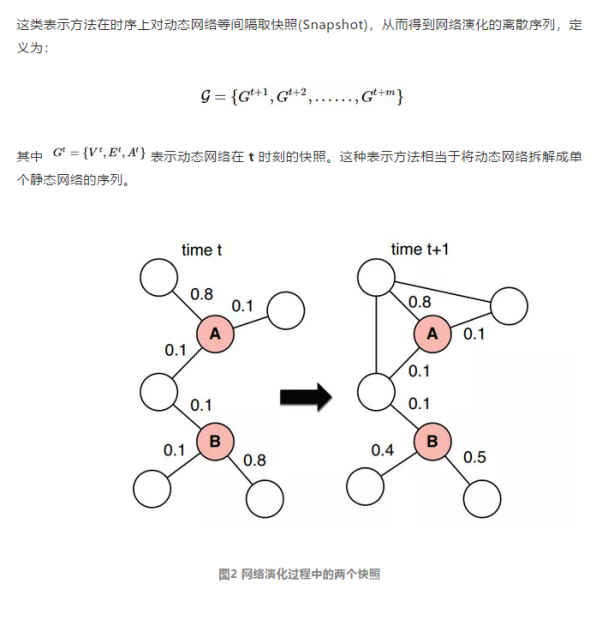
2.2 Continuous Time Network
三、动态网络的嵌入算法
动态网络的嵌入算法可以根据上面对动态网络的不同定义而分类。
对于上述两类,有文献分别称为collaboration networks和telephonecall networks,前者指网络拓扑结构随时间变化的动力学,后者表示网络上节点之间直接相互影响的动力学。为保持表述一致,下文仍采用本文的分类名称。
另一方面,几乎所有的动态嵌入算法都是从传统的静态嵌入模型修改而来,所以按照其基本的方法论,可以将动态网络嵌入算法分为:基于特征值分解的嵌入、基于Skip-Gram的嵌入、基于自编码器的嵌入和基于图卷积的嵌入。下面将按照这几种类型来介绍最新的动态网络嵌入算法。
3.1 基于矩阵特征值分解
对复杂网络的邻接矩阵$D$和属性矩阵$A$进行特征值分解,从而得到每个节点的嵌入表示,是一类古老传统但有效的嵌入方法。从矩阵的角度看,网络动态演变等价于原矩阵不断发生变化 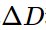 和
和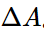 。而此类嵌入算法正是利用这些变化量,根据矩阵的摄动理论来更新网路的嵌入。
。而此类嵌入算法正是利用这些变化量,根据矩阵的摄动理论来更新网路的嵌入。
DANE
Li等人[1]在2017年提出的DANE模型就基于以上思路。首先,该模型将动态网络表示成Snapshots,并考虑网络的邻接矩阵和属性矩阵都会随时间变化的情况。而$t$时刻的动态网络嵌入是根据矩阵的变化量,在$t-1$时刻的嵌入基础上进行更新。对于$t=1$时刻,该模型提出一种结合矩阵$D$和$A$的嵌入算法作为热启动。其中,嵌入特征值和特征向量的更新公式如下:
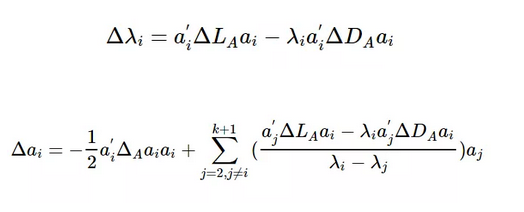
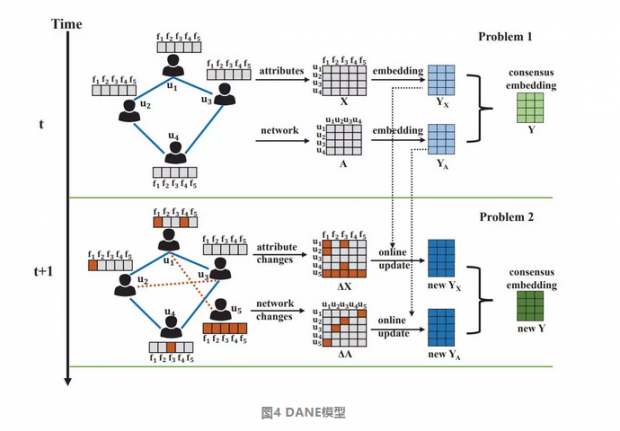
而整个模型可以图示如下:
DHPE
该论文由清华Cui老师[2]组发表在TKDE18,和DANE属于同期的工作,故思路也较为接近,也是讲动态网络表示成Snapshots。
本文基本基于他们组16年的文章Asymmetric Transitivity Preserving Graph Embedding,将其扩展到动态网络的处理上。
论文基于广义SVD分解(GSVD)和矩阵摄动理论(matrix perturbation),在保留高阶相似性的同时,动态更新动态网络的节点表示。
该论文额出发点在于:在保留网络高阶相似性的同时,当网络结构在下一时刻发生变化时候(增加/删除节点/边),如何快速有效的增量更新下一时刻节点的表示。
论文通过把Katz相似性转化为一般化的SVD分解,建模网络的高阶相似性,然后基于矩阵摄动理论动态更新网络下一时刻的节点表示。
其中,嵌入特征值和特征向量的更新公式如下:
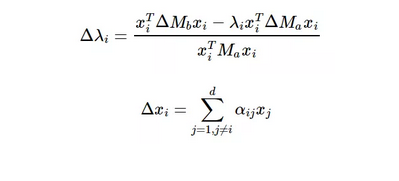
其他
还有17年清华Zhang等人[3]提出的TIMERS模型也属于矩阵分解的范畴,有兴趣的读者可以细度论文。
3.2 基于类Skip-Gram模型
14年Word2Vec的大热,使得Skip-Gram模型声名鹊起,而很多静态网络嵌入算法也是基于此模型,例如经典的Node2Vec和LINE。下面几项工作就是在该类工作上的动态拓展。
DNE
北京大学Du等人[4]在其15年LINE模型的基础上,提出了可分解的目标函数,使其能分别学习每个节点的嵌入,扩展出动态网络嵌入框架DNE。
还提出了更新节点的选择机制,大大的提高了嵌入更新的效率。DNE将网络表示成Snapshots,在每一时刻额嵌入能达到和LINE在该时刻重新训练一样的效果,并且效率更高。
另外,由于每次只对部分节点进行少量更新,所以不同时刻的嵌入相比重新训练的模型具有很强的稳定性。
对于节点多标签分类任务,该工作在多个实际网络上都表现优异。
CTDNE
该工作由Nguyen等人[5]发表于I3W 2018,思路非常简单,扩展性较强。
针对静态网络的嵌入通常是通过随机游走来得到训练语料,然后将语料交给Skip-Gram等模型得出网络的嵌入。但是上述的随机游走没有考虑到连边出现的时间顺序。例如,一条消息在网络中传播是有向的,但是无约束的随机游走可能得到反向的语料。
对于这点,该论文将动态网络表示成Continuous Time的形式,每条边具有多个时间戳,表示相应变化发生的时间。在此基础上,约束每次随机游走必须符合连边发生的时间顺序,从而将网络的时序信息捕获到随机游走的序列之中。
理论上,具有时序的随机游走序列集合是非时序的序列集合的子集。按照信息论的观点,时序信息的加入较少了嵌入的不确定性,也使得其在传统任务上的表现优于DeepWalk和Node2Vec等算法。
其他
基于类Skip-Gram模型的动态网络嵌入工作还有北航Zuo等人18年提出的HTNE模型[6]和Yu等人18年提出的NetWalk模型[7]。
前者通过节点的邻居形成序列(neighborhood formation sequence)建模节点的演变过程,然后利用霍克斯过程(Hawkes process)捕获历史邻居对当前邻居形成序列的影响。具体的细节,感兴趣的读者可以参考论文。
3.3 基于自编码器
以SDNE为代表的,基于自编码器的网络嵌入模型,因为其非监督的性质和较好的效果,一直被人们所青睐。将这类嵌入模型扩展到动态网络也是一件很直接的事情。南加州大学的Goyal今年便在此基础上前后做了两项工作。
DynGEM
Goyal在18年初发表了DynGEM模型[7],该模型基础是SDNE嵌入算法,同时也是将动态网络表示成Snapshots。DynGEM的想法也非常简单:为了保留上一时刻的嵌入信息,并为下一时刻所用,可以让下一时刻的嵌入模型直接继承上一时刻训练好的模型参数,如下图:
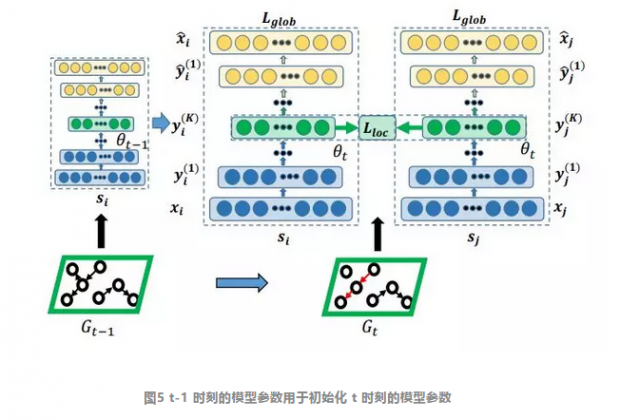
还有一点需要注意,网络的节点数目和连边多少对嵌入模型的架构有影响。所以文中利用启发式信息来根据新网络结构调整SDNE的整体架构,使其能适用于新网络。
dyngraph2vec
Goyal在18年下半年又发表了一篇动态网络嵌入的工作[8]dyngraph2vec( 是不是发现取名字也是技术活: )
这篇新工作diss了上一篇,说明了DynGEM框架和其他动态嵌入算法只考虑前一步的信息,而忽略了更加丰富的历史信息。
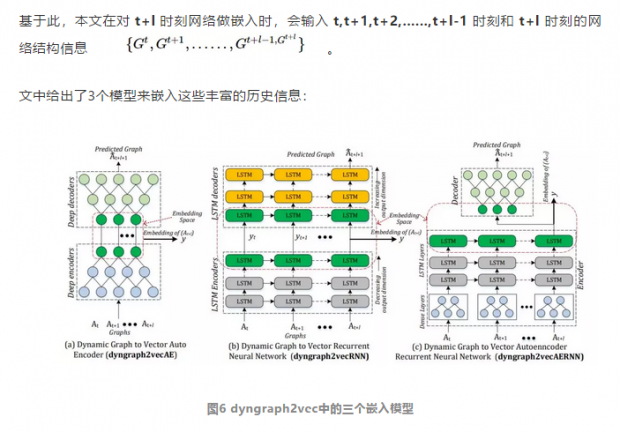
简单来说,本文是将时序的网络序列当做一段语料(将某时刻的网络结构类比于句中的单词),然后用RNN来编码历史信息。整体的嵌入框架仍旧是enc-dec的自编码器。
虽然想法是好,期望将尽可能多的历史信息用来嵌入当前时刻的网络,但是上述模型的算法复杂度比较大,不适合大网络的嵌入。
3.4 基于图卷积模型
图卷积(Graph Convolutional networks)是近年非常火热的网络嵌入模型,GCN,GAT,GNN和GraphSAGE都可以归到这一类别中。其核心思想在于利用节点(连边)邻居的信息来更新自己,通过迭代来扩大信息收集范围。
截止笔者写作本文(18/11/12),暂时没有看见很多基于图卷积的动态网络嵌入算法。只有一篇佐治亚理工学院Trivedi等人正在ICLR2019双盲审阶段的工作DyRep[10]。下面就对这篇文章做简要介绍。
DyRep
这篇文章考虑了网络上的两种动态过程:Association Process和Communication Process。前者代表了网络拓扑结构的变化,后者表示了网络上动力学的变化。而文中定义了“事件”来统一表示上述两个过程的变化。DyRep将节点Representation的变化看做是上述两个过程相互影响的中间桥梁,从而能根据新的事件不断更新节点的表征。当一个事件发生时,节点的新表征由事件相关的邻居节点聚合得到。
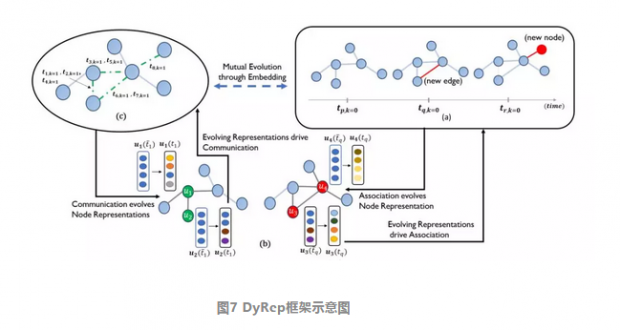
值得注意的是,模型中聚合节点邻居是还采用了注意力机制。
3.5 其他动态嵌入模型
除了上述几类模型之外,还有一些从全新的视角来处理动态网络的工作。笔者无法简单的归一到上述某一个类别。
Dynamic Triad
浙江大学Zhou等人在18年的工作Dynamic Triad[11]对于动态网络的建模很有新意。通过复杂网络分析中的三角闭合问题,建模动态网络的演变,很好的描述了网络的变化。
在复杂网络的研究中,网络结构的变化被认为是导致网络上动力学的主要原因之一。而三角闭合问题是网络结构变化最重要的体现之一。
简单地说,对于任意3个点,若相互被两条边相连,则称之为开三角,若两两互连,则称之为闭三角。网络结构演化的一大特征便是开三角随时间有可能变为闭三角。
如果节点的表征能预测出网络结构的这种变化,则有理由相信节点的嵌入捕获了相关的动态信息。
而这篇工作就是基于上述想法,构建了预测三角变化的Loss函数:
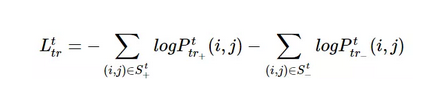

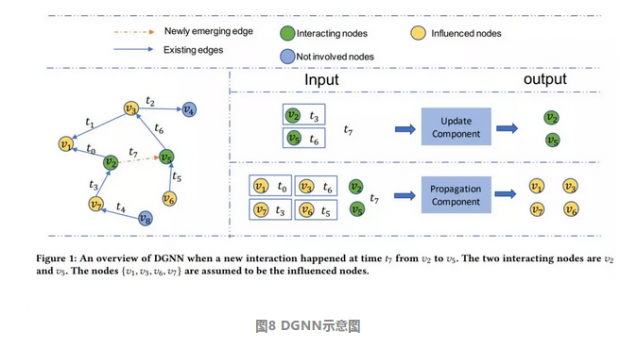
DGNN
Ma等人[12]今年发表的工作DGNN更加细致的考察了连边作用时间与其对网路嵌入影响之间的关系。

Summary
网络嵌入算法在近几年异常火热,因为其在图结构或网络数据分析中的潜力是巨大的。
但是新兴的算法并没有成熟的应用,原因在于两点:
-
一是因为很多实际网络都巨大无比,模型的训练花费的时间难以想象;
-
二是本文提到的原因,也就是实际网络大多数动态的,直接用静态嵌入算法来处理并没有太好的结果。
研究者们也认识到这些问题,所以今年(18年)出现了相当多关注动态网络嵌入的工作。但是如前文所概述,很多工作都是基于静态网络嵌入框架修改而来,存在很大的局限性。对于动态网络也没有统一的的表示规范。虽然也有一些新的想法,但是还没有像DeepWalk和GCN那样的标杆性工作出现。
参考文献
1. Li J, Dani H, Hu X, et al. Attributed network embedding for learning in a dynamic environment[C]//Proceedings of the 2017 ACM on Conference on Information and Knowledge Management. ACM, 2017: 387-396.
2. Zhu D, Cui P, Zhang Z, et al. High-order Proximity Preserved Embedding For Dynamic Networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2018.
3. Zhang Z, Cui P, Pei J, et al. TIMERS: Error-Bounded SVD Restart on Dynamic Networks[J]. arXiv preprint arXiv:1711.09541, 2017.
4. Dynamic Network Embedding : An Extended Approach for Skip-gram based Network Embedding
5. Nguyen G H, Lee J B, Rossi R A, et al. Continuous-time dynamic network embeddings[C]//3rd International Workshop on Learning Representations for Big Networks (WWW BigNet). 2018.
6. Zuo Y, Liu G, Lin H, et al. Embedding Temporal Network via Neighborhood Formation[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018: 2857-2866.
7. Yu W, Cheng W, Aggarwal C C, et al. NetWalk: A Flexible Deep Embedding Approach for Anomaly Detection in Dynamic Networks[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018: 2672-2681.
8. Goyal P, Kamra N, He X, et al. DynGEM: Deep Embedding Method for Dynamic Graphs[J]. arXiv preprint arXiv:1805.11273, 2018.
9. Goyal, Palash, Sujit Rokka Chhetri, and Arquimedes Canedo. "dyngraph2vec: Capturing Network Dynamics using Dynamic Graph Representation Learning." arXiv preprint arXiv:1809.02657 (2018).
10. Trivedi R, Farajtbar M, Biswal P, et al. Representation Learning over Dynamic Graphs[J]. arXiv preprint arXiv:1803.04051, 2018.
11. Zhou L, Yang Y, Ren X, et al. Dynamic Network Embedding by Modeling Triadic Closure Process[C]//AAAI. 2018.
12. Yao Ma, Ziyi Guo, et al. Streaming Graph Neural Networks //
13. Mitrovic S, De Weerdt J. Dyn2Vec: Exploiting dynamic behaviour using difference networks-based node embeddings for classification[J].
作者:高飞
编辑:王怡蔺
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 