Barabási组最新Nature封面文章：复杂网络如何3D打印？-集智俱乐部的财新博客-财新网

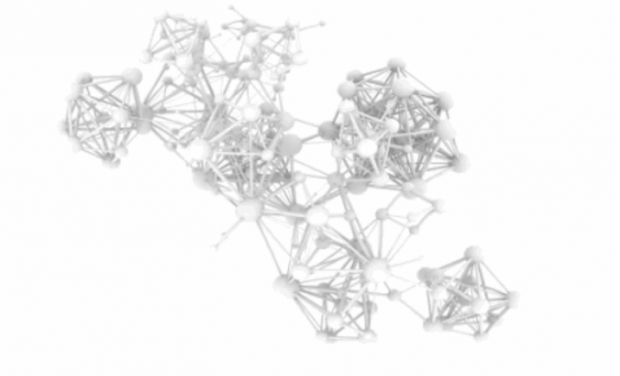
采用新提出的3D空间布局模型的两个网络，经3D打印之后的实物图。左：BA网络模型，右：ER网络模型

导语

3D打印复杂网络，不仅是技术，更是艺术。近期Nature杂志以封面文章的形式发表了以复杂网络巨擘 Albert-László Barabási为通讯作者，Dehmamy为第一作者的研究成果[1]，详细讨论了在真实世界中，网络的节点和边所占据的体积、大小不能忽略的情况下，如何在3D空间上对网络进行布局。

论文题目：

A structural transition in physical networks

论文地址：

https://www.nature.com/articles/s41586-018-0726-6

自从1736年欧拉解决柯尼斯堡七桥问题，并创立图论，以及最近几十年复杂网络的研究热潮兴起以来，大多数的研究都基于对现实世界的复杂系统进行抽象，构建相应的图或网络进行理论研究。

而这篇论文反其道而行，探索了如何将比较抽象的网络还原到真实世界中去，着重探索了2D空间的网络在3D空间中的布局问题。通过这篇文章你会发现，如果以前的研究是科学与技术，那么，网络在3D空间中的布局问题，简直就是一种艺术！

2D网络局限性

长期以来，为了让理论研究变得简洁方便，我们通常会把实体的复杂系统抽象成网络（或图）的结构——即把系统中的实体抽象成与其大小、形状无关的“点”，而把连接实体的线路抽象成“线”，称为边。这样的网络中，节点与边的位置及大小可以随意移动和调整。这给了理论研究非常大的灵活性。如下图中2D布局迥异的两个图实际上拥有相同的结构（即图同构[2]）。

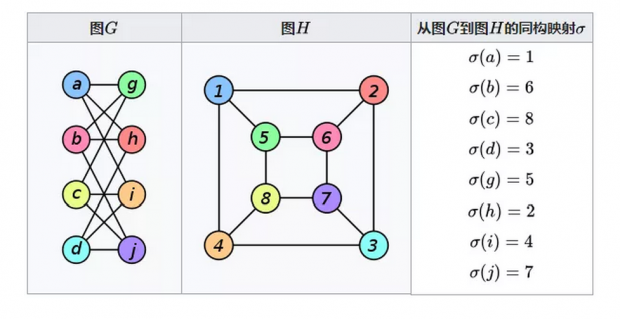
但在实际的一些应用研究中，这种简洁的抽象网络也会存在很大的缺陷。比如，在研究大脑中神经元网络的结构与功能、蛋白质相互作用，3D集成电路等一些网络时，不仅要考虑节点与边的大小、粗细等属性，还要考虑他们的空间3D布局。更严格一点，若要求所构建的复杂系统的边不能有交叉或重叠（overlap），则以前简洁抽象的网络模型就难以直接在现实中使用。

研究表明，当网络中节点的大小和边的粗细不可忽略时，随着节点越来越大，边越来越粗，网络会显得愈加“拥挤”，网络中点边之间的穿插情况会越来越多。如下图所示，在一个20个节点的BA网络中，随着边越来越粗，发生穿插的边数越来越多。由于网络的有限性，在最后阶段发生穿插的边数会趋于稳定。

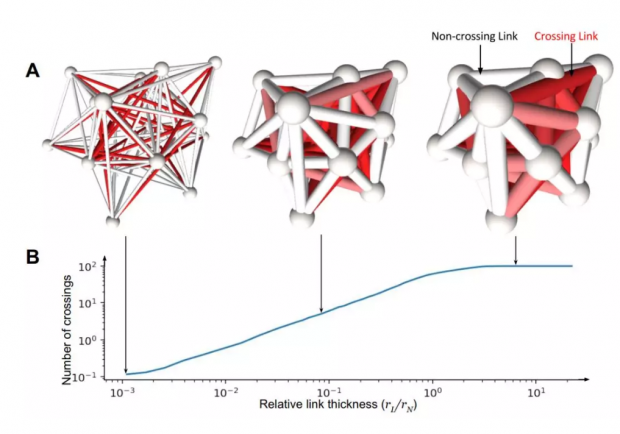
显然，穿插状况频发的网络在实际应用中（比如3D打印）会有很大局限性，会影响系统的几何结构、演化与动力学功能。

如何避免互相穿插

Dehmamy等人研究了不可穿插条件（non-crossing conditions）如何影响网络的实际结构[1]，特别是如何影响网络中所有边的长度——在实际的复杂系统中，边长越长往往意味着系统成本越高。

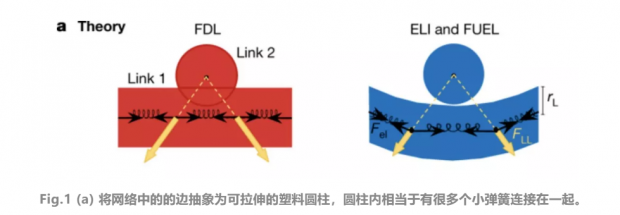
Dehmamy等人将节点抽象为塑料圆球，边抽象为一个塑料圆柱。这样，边不必保持笔直，节点也不必保持标准的圆球形状，而是可以发生形变。边（或点）通过形变，避免结构上的穿插（如Fig. 1(b) 所示）。

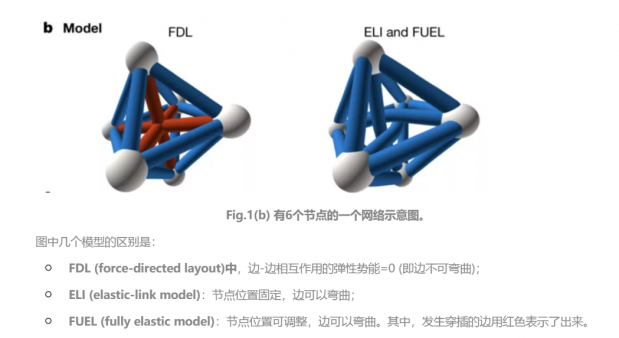
每条边在发生形变时，每条边受到内部的弹力作用和外部的斥力作用（如Fig. 1(a) 所示）。基于此，作者借用自回避聚合物链（self-avoiding polymer chains）和流形动力学（manifold dynamics）中常用的势能计算方法，定义了网络发生形变之后的总势能V，包括：网络中所有边的总弹性势能，点-点相互作用的弹性势能，边-边相互作用的弹性势能，以及点-边相连产生的势能。

作者认为，当网络的总势能V最小时，网络的总边长最小。要让网络总势能最小，可以将产生形变的网络浸入高粘度介质中，让网络相对稳定地、慢慢地松弛到低能状态，此时便得到了在不可穿插条件下，网络的边长总和最短时的网络结构。

然而，求解全局最小总势能是NP hard问题，所以Dehmamy等人用模拟退火算法寻找局部最优解，结果如Fig. 1(c) 所示。

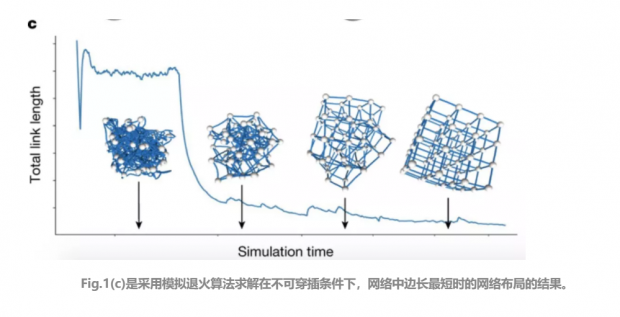
当调整网络中边的粗细的时候，可以发现(a) 网络中穿插的边数随着塑料圆筒半径r_L的增长而线性增长; (b)在塑料圆筒的半径r_L较小的时候，网络的总边长与圆筒半径的大小无关；(c) 在塑料圆筒的半径r_L较小的时候，网络中的边的曲率变化不是很明显。

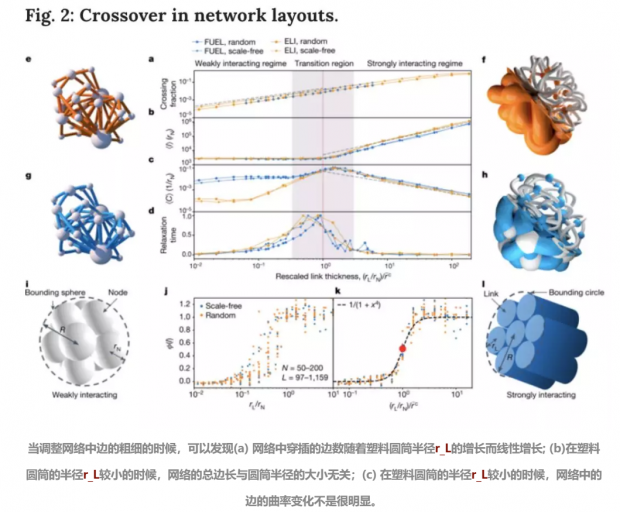
强弱连接影响网络3D布局与功能

然而，上图结果也表明，当边的半径超过一个临界值，即强连接情况下(the strongly interacting regime), 一切都会不同。由于边的半径比较大，为了避免边之间的穿插，网络中的边往往不得不在有限的空间内蜿蜒起伏，“在夹缝中求生存”，如图Fig. 2 (f), (g)所示。并且，在半径较大的时候，网络的总边长不再与半径无关，而是随着半径的增长而线性增长。

既然强连接和弱连接情况下的网络布局如此不同，很自然的一个问题就是，当边的半径是多少的时候，网络是强/弱连接的？

作者通过计算得出，当网络的边的半径与节点的半径的比值小于N^-6时，网络是弱连接的情况(the weakly interacting regime)，其中，N是网络中的节点数。当N趋于无穷时，，即在热力学极限下，网络不存在弱连接的情况！并且，这一结果与网络的类型、网络度分布、网络的规模无关。

也就是说，当网络节点较多时，传统的网络布局/可视化方法由于不考虑边的粗细，且边大多数情况下保持笔直，会让网络充斥着大量交叉着的边，难以在实际应用中使用。

最后，作者通过柯西应力张量（Cauchy stress tensor）计算了弱连接情况和强连接情况下，网络单位面积所承受的作用力。

在弱连接情况下，网络中的边比较细且几乎保持着笔直的状态，系统中的势能主要为点-点相互作用的弹性势能，以及点-边相连产生的势能。面对外部压力时，网络表现得更像固体（如图Fig. 3 (a)所示）。

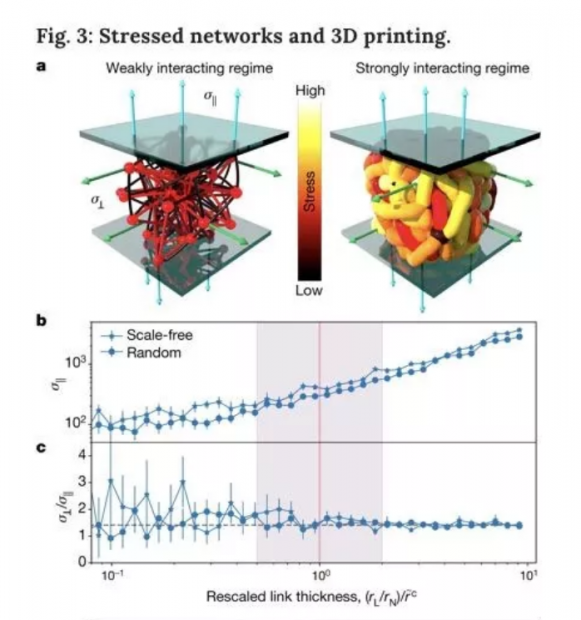
在强连接情况下，网络中的边比较粗且蜿蜒曲折，几乎占据了整个网络布局的大部分体积。此时，系统中的势能主要包括网络中所有边的总弹性势能，以及边-边相互作用的弹性势能。面对外部压力时，网络表现得更像液体或凝胶（如图Fig. 3 (a)所示）。

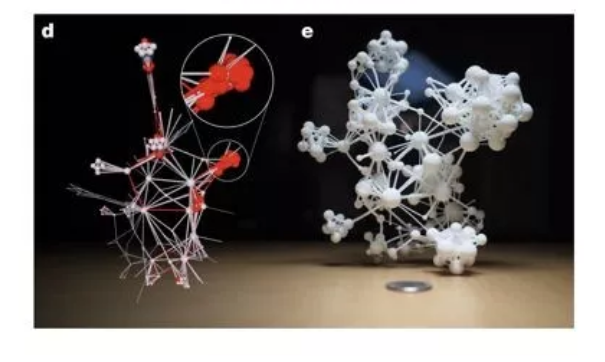
图中(d), (e) 分别是用FDL模型、FUEL模型对一个网络的可视化。可以看出，FDL模型中，由于节点位置固定且边比较密集，产生了很多相互穿插的边。这些相互交叉、覆盖的边使人们无法清晰看到网络的详细结构。而FUEL模型则较好地展现了网络结构上的详细细节。

在最后，推荐给大家一个由本文作者建立的、超级炫酷的3D复杂网络可视化网站可以让你和设计师一样，近距离超逼真地观察网络的每一个细节：

http://netwonder.net

参考资料：

[1] Dehmamy N., Milanlouei S.& Barabási A. A structural transition in physical networks, Nature 563:676–680 (2018).

[2] https://en.wikipedia.org/wiki/Graph_isomorphism

[3] http://netwonder.net

备注：

本文中的网络数据与代码地址：

https://github.com/nimadehmamy/3D-ELI-FUEL

作者：任晓龙、吴蕾蕾

编辑：王怡蔺

话题：