不用繁琐公式，如何预测复杂的混沌系统？-集智俱乐部的财新博客-财新网

导语

一提到预测复杂系统的变化，你想到的可能是蝴蝶效应、混沌理论、洛伦兹吸引子……等等数学方法，但生态学家避开了复杂公式，开发出了一套简单有效的 R 语言软件工具。

编译：集智俱乐部翻译组

来源：Quanta Magazine

原题：A Twisted Path to Equation-Free Prediction

预测海洋渔业：经验动态建模破解难题

有时候，我们无法解释生态数据。一个典型的例子是在加拿大Fraser河产卵的红鲑鱼。科学家从1948年就开始追踪该渔业，期间经历了无数起起落落。最开始，鲑鱼数量看起来与洋流温度呈负相关：每隔数十年，北太平洋面从暖变冷，鲑鱼数量随洋面温度的升高而降低。这个发现能说服生态学家，因为鲑鱼在冷水中数量暴增。为了避免鲑鱼灭绝，渔业管理人员也根据洋面温度和鲑鱼数量的公式设立捕捞限额。

但是在20世纪70年代，一件奇怪的事情发生了：洋面温度和鲑鱼数量不再同步。所谓两变量的紧密关联实际并不存在，鲑鱼数量看起来是随机波动的。

在生态学家George Sugihara看来，仅凭粗浅的生物学知识经营一家大型渔场愚蠢而鲁莽。现在，他和他的同事解决了Fraser河鲑鱼之谜。他们的主要突破是？——摈弃公式！

Sugihara的团队提出了混沌系统中的经验动态建模（empirical dynamic modeling），该建模不需要做出任何关于鲑鱼生物学的假设，只需要输入原始数据。在建模设计的过程中，这些科学家们发现，虽然没有线性关联，事实上，海洋表层温度可以预测鲑鱼数量的波动。Sugihara称，经验动态建模能够揭露：自然界大量存在的复杂系统中的因果关系。

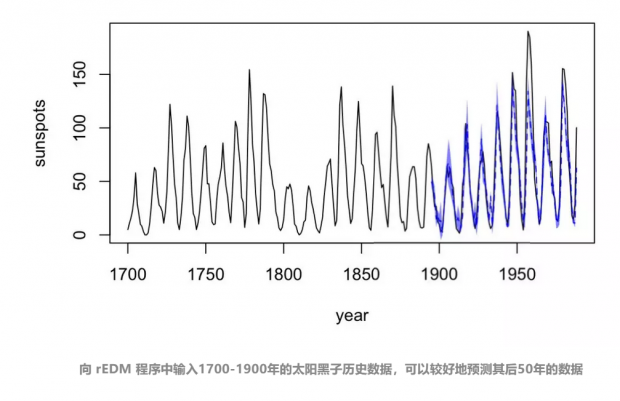
2015年，Sugihara和他的同事在美国国家科学院院刊（PNAS）发表报告，预测2014年Fraser河鲑鱼数量。经验动态建模预测鲑鱼数量在4500万到9100万之间，实际值大约8800万，比其他方法都要准确，例如太平洋鲑鱼委员会的预测是6900万到2亿。同样的成功也发生在太平洋沙丁鱼和海湾和大西洋的门哈登鱼上。准确预测好处很多，比如，渔夫可以知道接下来的捕鱼机需要多少渔船。

相关论文：Equation-free mechanistic ecosystem forecasting using empirical dynamic modeling

地址：

https://www.pnas.org/content/112/13/E1569

渔夫正在装载渔网，为Fraser河红鲑鱼渔场的开放做准备 | 摄影：Richard Lam

追溯原理：混沌系统的嵌入定理

经验动态建模的根源，要回到30年前。混沌理论盛行于20世纪60年代，科学家发现，许多自然的复杂现象无法预测。在混沌系统中，微小的扰动可以产生巨大的、似乎不可预测的影响，比如，蝴蝶轻扇翅膀，能够影响千里之外的天气。

“神秘的不是世界本身，而是我们看待世界的方式。”

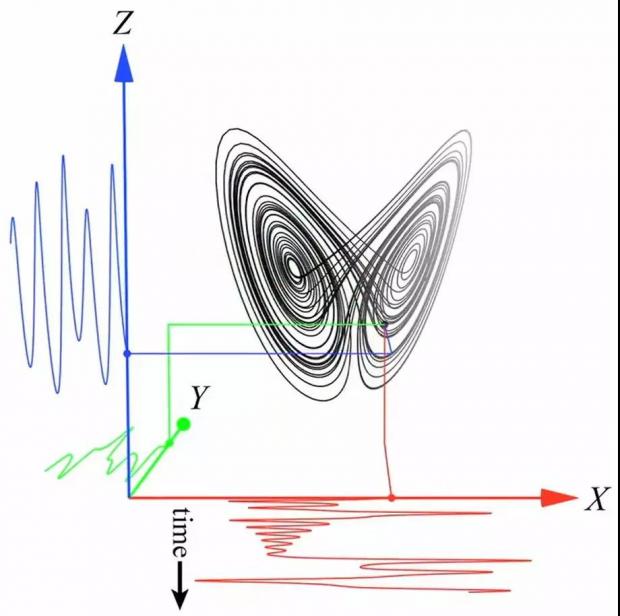
在20世纪70年代，荷兰数学家Floris Takens试图在混沌中发现秩序。Takens和物理学家David Ruelle一起提出了“奇异吸引子”（strange attractor）的概念：在影响系统的变量组成的坐标系中，存在着一些点，随着时间的推移，就像纱线绕轴，系统中的其他点会围绕着它们旋转。

但是，在很多自然系统中，组成坐标系的相关变量数是无限的，比如一时一地的天气；而且有些变量很难测量，例如北极上空三英里的气压。

不过我们总能持续准确地测量一个变量。以如纽约市的温度为例，Takens发现，利用一变量现在和过去的值可以推得坐标系中的其他信息。这种方法需要构建一个由单一变量的过去测量值组成的坐标系，一个坐标轴是时代广场今天的温度，第二个坐标轴是昨天的温度，第三个是两天前的，以此类推，如下图。

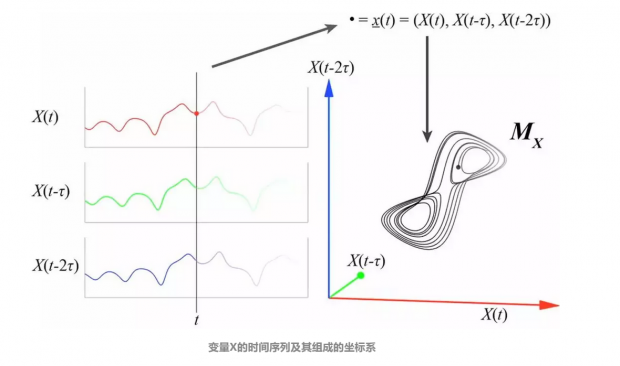
Takens发现，混沌系统的整体状态，至少在理论上，可以嵌入单一变量的时间序列，在1981年，Takens发表了“嵌入定理”（embedding theorem），经验动态建模可以通过其中一个变量的发展轨迹推出整体形状。

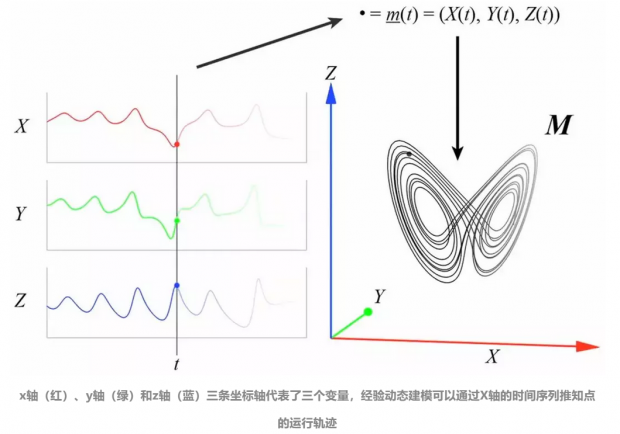
嵌入定理：通过单一变量的时间序列可以推知混沌系统的整体状态

延伸阅读：

https://cnx.org/contents/k57_M8Tw@2/Takens-Embedding-Theorem

乔治梅森大学的Tim Sauer称，该定理“引发了热烈的讨论”。

下一步就是在现实中应用“嵌入定理”，但是Takens纯粹的数学公式难以应用在杂乱的自然中。虽然天气推动了混沌理论的建立，仍然不能预测它。因为天气涉及了太多持续变化的变量，而且无法真正测到哪怕一个变量。Sauer说，Takens的定理在变量较少的系统中更有用。

Tim Sauer，弗吉尼亚州费尔法克斯郡乔治梅森大学（George Mason University）的数学家，扩大了“嵌入定理”的应用领域

Sugihara跟从Robert May学习Takens的“嵌入定理”。1990年，Sugihara和May在Nature上发表了一篇论文，关于如何运用Takens的“嵌入定理”，预测一些非线性系统的短期演变。核心方法是识别系统吸引子图中靠近系统目前状态的点。经过一两个单位时间，通过过去的行为，可以预测系统的相似演变。这篇论文的引用已过千，遍及各学科。这篇论文也促使Sugihara在职业生涯的中期涉足金融领域，用类似生态学中的经验动态建模来预测股价。

Hao Ye等人根据嵌入定理，编写了一个开源的 R 语言软件包——rEDM，来实现经验动态建模（Empirical Dynamic Modeling）| 地址：https://github.com/ha0ye/rEDM

经验动态建模的基本机制。视频展现了时间序列和动态吸引子之间的关系，并说明了如何利用Takens嵌入定理重建整体运动轨迹。

生态学应用：公式模型 vs 经验动态建模

近一世纪前，提现了第一个生态学模型，自出现起就深受物理学和工程学影响。在过去200年间，也提出了许多描述系统演化的微分方程。比如，最常用的渔业模型是加拿大生物学家William Ricker于20世纪50年代提出的Ricker模型，预测现有鱼群次年的出生率。渔业管理人员仍然高度依赖Ricker模型，通过包括温度的变量，预测不导致鱼类资源锐减的“最高持续产量”。

Sugihara指出，这样的预测太过简单，Ricker模型假设鱼群数量与环境因素的关系是线性且静止的，然而包括气候、洋流和人类活动这些环境因素是持续变化的，“而且Ricker模型不会随着样本量的增大而优化”。

相反，只要加入新数据，经验动态建模就会得到优化。当数据量足够形成密集的吸引子时，Takens的“嵌入定理”表现的最好，更容易发现接近过去的当前状态。任何新的数据点都会帮助使用者预测系统的优化。

Sugihara的研究不是“扶手椅上的数学”（指脱离实际应用），科研人员都可以使用Sugihara的程序，Sugihara的学生还开办了教授使用方法的讲习班。

顶尖生态学家希望能将Sugihara的方法应用于更需要预测的其他生态系统，不止在海洋渔业上。美国地质调查局迈阿密分局的生态学家Don DeAngelis称经验动态建模为“重大理论突破”。DeAngelis几乎一生都在使用公式建模，也说他希望在工作中用Sugihara的方法预测佛罗里达大沼泽地的鱼群数量变化。

建模局限：数据、稳定性、短期

虽然在医药和神经科学等领域，正以超出科学家处理能力的速度喷涌着巨大量的数据集，然而，经验动态建模的数据缺乏仍未解决，生态学依旧在通往大数据革命的路上艰难前行。

Sauer指出，更为困难的问题在于经验动态建模的稳定性（stationarity）。我们不确定，一天后，一年后，十年后，或者仅仅是下一次，建模是否还具有测量意义。稳定性是实验室科学的标志：现在的蛋白质分子或酵母细胞和一世纪前一模一样，但是，2015年和1950年指的“Fraser河红鲑鱼”是同一种鱼吗？在这段时间内，加拿大渔业海洋部曾经改变过鲑鱼种群的定义；而且，鱼类本身也会进化。

此外，DeAngelis指出，经验动态建模只能做出短期预测。回到混沌系统的基本问题：两系统如果初始条件错之毫厘，演变轨迹就会差之千里。实践意义上，即使该建模能够很好地预测明年的鲑鱼数量，也不能从今年起预测数年后的鲑鱼的数量。

终结公式建模：转向复杂非线性系统

因为上面提到的和其他原因，Sugihara开始推广经验动态建模，应用于生态学以外的其他领域。Sugihara等人将该建模应用在金融学，神经科学，甚至基因学中。这些领域都涉及复杂而持续变化的现象，很难或不可能用近300年来主流的公式建模来预测。DeAngelis称，经验动态建模很可能是复杂系统研究的未来。

DeAngelis甚至走的更远。在2015年发表于PNAS的评论文章中，DeAngelis指出：长期以来，主流科学都使用公式建模，经验动态建模可能是转变的一部分。许多评论家认为，公式没有在生态学中取得和物理学一样的成功，生态学需要全新的研究方法。

相关论文：Equation-free modeling unravels the behavior of complex ecological systems

地址：

https://www.pnas.org/content/112/13/3856

Sugihara同意DeAngelis的看法，静态平衡的公式在工程上可能很有用，但是，对于自然界中的复杂非线性系统，是时候摈弃这种静止的观念了。Sugihara观察到，一段时间内可能会出现很有诱惑力的线性相关，但是在混沌系统中，这种相关性是错误的，如前所述：“神秘的不是世界本身，而是我们看待世界的方式。”

几年前，Sugihara收到了分子生物学家Gerald Pao的邮件。隶属于Salk生物研究所Inder Verma实验室的Pao确信，Sugihara的方法可以用于解释基因表达的数据。

相似的应用也发生在神经科学领域。神经科学家可以预测癫痫等后果严重的疾病的发作，其中一些通过Takens的嵌入定理构建神经元网络的激发模式。Sauer表示，相比生态学家，神经科学家可能更容易应用该定理，但是，“真正的杀手级应用还未出现”。

Sugihara也同意Sauer的判断：“Takens的嵌入定理很神奇”，但是，“它潜在的应用前景尚未得到充分的认识。我认为这只是转变的开始……我认为我们正在克服壁垒。”

编译：杨清怡

审校：李周园

原文：

https://www.quantamagazine.org/chaos-theory-in-ecology-predicts-future-populations-20151013

rEDM包：

https://github.com/ha0ye/rEDM

话题：