21世纪社交图鉴：网络科学“支配”下的网游玩家行为模式-集智俱乐部的财新博客-财新网

导语

研究发现“冤家宜解不宜结”、“投桃报李”、“以牙还牙”等等真实世界中的行为规律在社交网游中依旧遵循，这引发了维也纳医科大学教授 Stefan Thurner 的大胆猜想：我们是否可以根据虚拟世界里的社交数据构建模型，收集并替换足够充分的真实数据之后再应用于现实的行为预测中呢？

论文原题：

Virtual social science

论文地址：

https://arxiv.org/abs/1811.08156

孔德的远见：社会物理学

早在十九世纪初期，法国著名的哲学家，社会学、实证主义的创始人：奥古斯特·孔德（Isidore Marie Auguste François Xavier Comte）提议到：借鉴物理学的实证方法去建立社会科学。他将这一在当时看来“前景渺茫”的学科称为『社会物理学』。可惜的是，当时并没有人响应他的号召，最终孔德在贫困潦倒中遗憾过世。

不得不承认，在那个没有计算机、统计学不成熟的时代，孔德的失败实属必然。其一，人们无法理解社会成员之间相互作用的原理；其二，无法汇总到足够多的数据，去对理论进行验证解释。

传统研究中，社会科学主要依靠定性的描述，难以定量计算、难以重复、难以验证。两百多年后，二十一世纪的今天，数据规模与计算能力不再是定量的约束，我们得以重拾孔德的愿景，把严谨的数理计算纳入到社会学，把社会学变为实验科学：可定量、可预测、可试验。

虽不一定能够成功，且这样的尝试固然会遭到传统社会科学的批评，但现在的社会物理学研究已经有了一些显著的成效。在本文所研究的网络游戏社会中，我们能够记录社交系统的每一次一个人所有时间的全部互动。

网络游戏中的虚拟世界

维也纳医科大学的复杂系统科学教授 Stefan Thurner 在他的论文 Virtual social science 中分析了网络游戏 Pardus 的数据，并就此发现在虚拟的网络社交中也符合传统社会中的基本原理。

网络游戏 Pardus 是一个基于科幻小说改编的网络游戏。游戏构建了一个未来的世界，玩家通过“虫洞道路”在“星系扇区”中穿梭，玩家间可以自由社交，确立彼此的敌对-友好关系，进行贸易物品交换，与他人进行社交发送私信（PM），甚至加入联盟，同时也可以参与联盟的战斗，或者是成为一名赏金猎人。

在本论文的探究中主要关注玩家间的六种相互作用：通信、贸易、交友、敌对、攻击以及悬赏。

社会系统与复杂网络

社会系统，不断地演化，存在路径依赖，存在不均衡、甚至与其他环境相关。因此可以说社会系统是一个复杂系统，一个随时间变化的多层交互网络，即协同演化的多层网路（co-evolving multilayer network）。

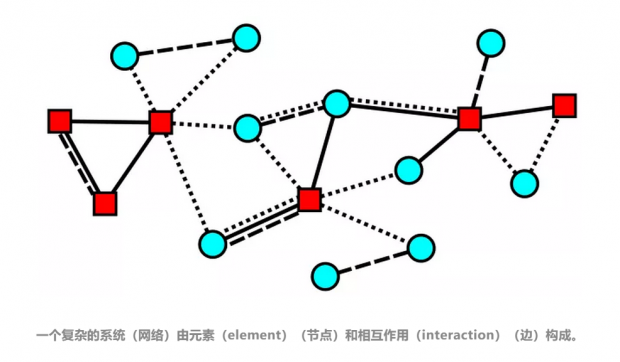
上图就展示了一个多层的网络，每一个元素包含两类，四种状态（颜色：红、蓝；形状：方、圆）。相互作用的类型有三种（实线、虚线、点划线）。协同演化就是指网络中的节点和边能够互相影响，改变彼此的状态。

节点状态（state）可以用一组向量表示比如上例中的 <颜色，形状>。相互作用会是一个随时间变化的量，这个量的强度通常与相互作用的“事物”的数量有关。

节点状态的变化可以是随机独立的也可以是确定的，在多层的网络中这种变化可能是单层网络内部导致的，也可能是多层共同导致的结果。在网格中他们会受到彼此的影响。

节点的变化与边的变化往往不是独立的，二者互相影响，形成协同演化（co-evolve）。网络的状态（拓扑结构、权重等等）决定了未来的节点和边的状态，而反过来，节点和边的状态也决定了网络自身的未来状态。

这样的复杂系统有诸多特点：系统演化是非线性的过程、依赖于环境给出的“上下文”、能归纳抽象为算法、存在路径依赖、且有记忆性。

虚拟游戏中的网络科学

弱连接（weak tie）

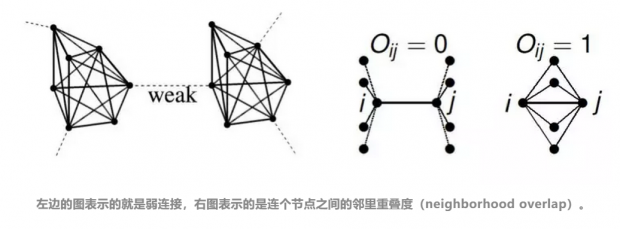
上图表示的是两个人之间的关系（tie）的强度是由双方共同好友决定的，共同朋友很多意味着他们之间的连接是一个强连接。然而，如果如上图所示，二人根本没有任何的共同好友，那么可以或二人之间的连接是一个弱连接，或者说，去除掉弱连接所对应的这条边，上图可以被分为两个独立的子图。再换而言之，这二人的关系，为两个群体搭建起了桥梁，或者是说捷径。

也意味着，这样的连接是这个网络中成员联系的一条“必由之路”也就是连接的介数（link-betweenness）高。两个节点间的弱连接就存在于连接的介数中。在本文的虚拟社交网络中连接介数与重叠度成开平方反比的关系，这一点与真实社会的电话通信网络的数据相一致。弱连接假说在 Pardus 社会中得到了证实。

三元闭包（ triadic closure）

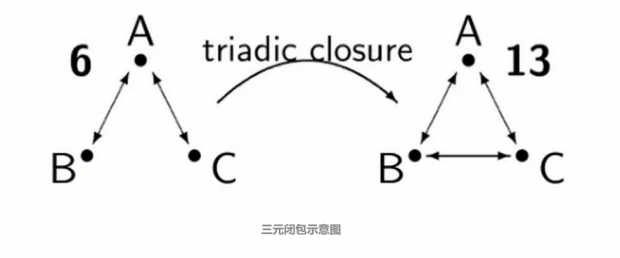
三元闭包反应的是一个常见的社会现象，如上图所示 B 和 C 都有共同的朋友 A ，因而 B-C 之间建立友谊的可能性也会提高。三元闭包反映出了一个网络随时间变动的可能性。

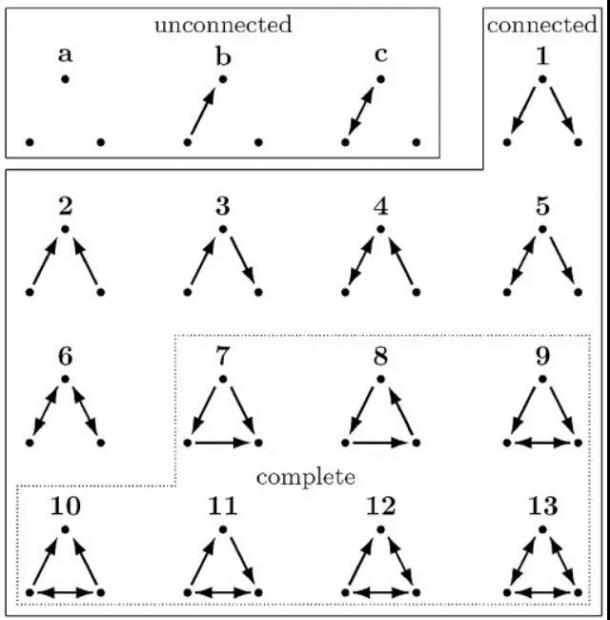
在网络中能够产生的几种关系，从缺乏连接，到建立连接，到链接稳定的状态。

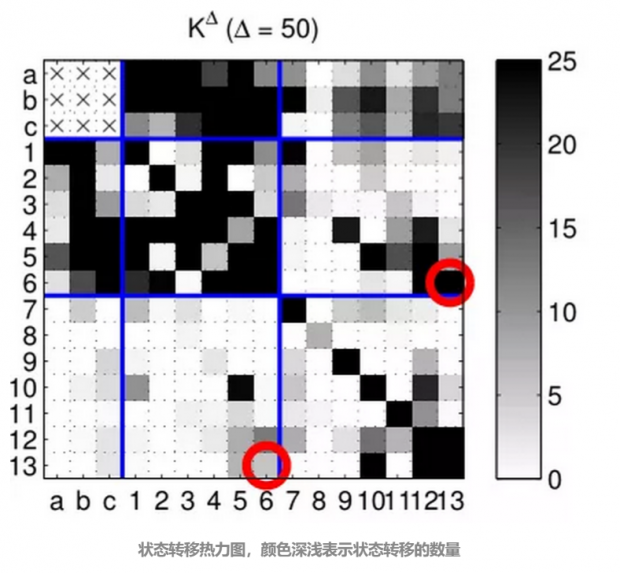
图中的红圈表明：6->13 这样的状态转变明显多于 13->6。这一点也说明了，三元闭包是一个稳定的状态。

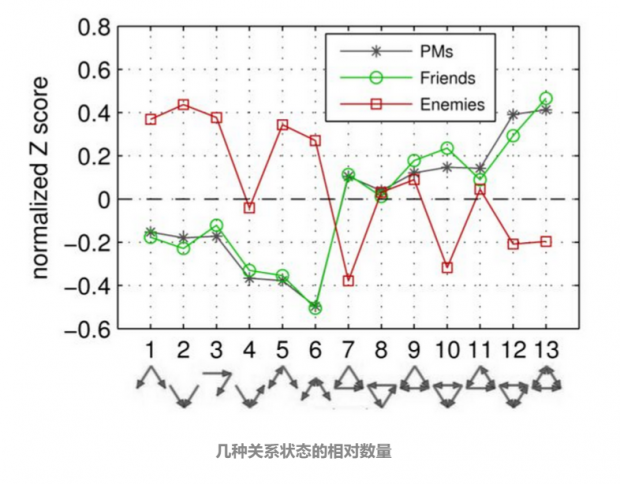
Stefan Thurner 用 Z 分数来表示网络存在三元闭包时的网络结构与随机网络结构相比数量的相对多少。我们能看到，对于积极的网络（友谊网络），缺乏链接的结构明显较少，绝大多数网络够能够形成完整稳定的三元闭包，这一点与我们在生活中的认识是相符的，朋友的朋友也确实能成为新的朋友。

而对于消极的网络（敌对网络），更多的是链接不稳定的网络结构，稳定的三元闭包关系较少。玩家在网络游戏中也遵循了“冤家宜解不宜结”这句老话。

社交结构平衡

结构平衡：一个由 A、B、C 三人组成的网络如何才能到达平衡状态。其中 + 表示朋友，- 表示敌人。

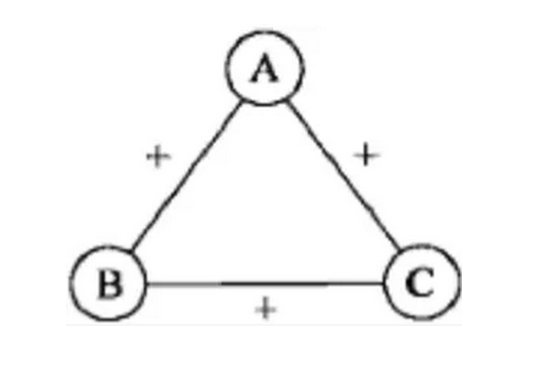
第一张图中，A、B、C 三人都是朋友，这自然是一种稳定的平衡状态，符合我们在社会中能见到的“朋友的朋友是朋友”这样一个规律。

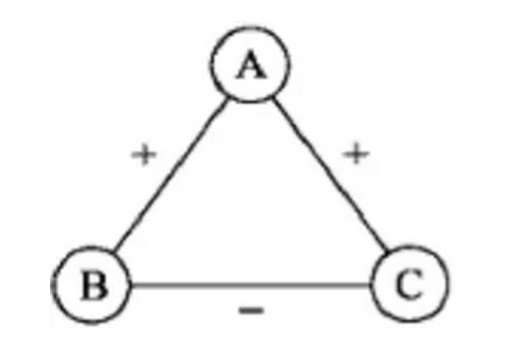
第二张图中，A、B、C 三人中，AB、AC 是朋友，而 BC 是敌人，在这样的一个关系中，我们可以想象 A 这个中间人就处于一个比较为难尴尬的处境，这样的关系就比较不稳定，也许 A 能够化解 BC 间的矛盾，三人都成为朋友，或者 A 放弃“中立”的政策，完全倒向其中一方，二人一致对外。因此说这是一个不稳定的状态。

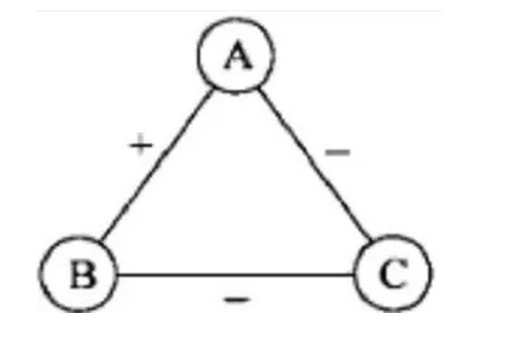
第三张图中，A、B、C 三人中，AB 是朋友，AC、BC 都是敌人，这也是一个一个稳定的平衡状态，与“敌人的敌人就是朋友”这个道理是相符合的。

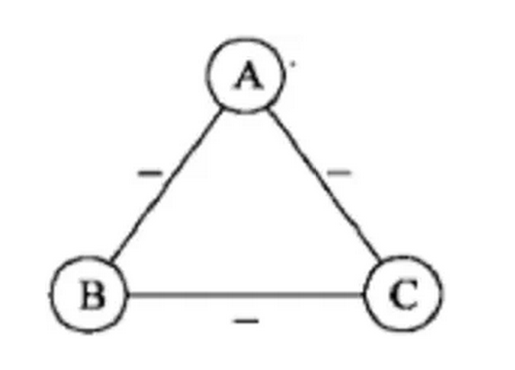
第四张图中，A、B、C 三人都是敌人，这自然也是一种稳定的状态，虽然人与人国家与国家之间彼此设防的状态比较常见，但在现实中，这样的状态也不稳定，以三国为例，魏蜀吴三国鼎立，本质上是互相为敌的，但诸葛亮却提出了“联吴抗曹”的战略，共同对抗一个敌人，从而向一个稳定的状态转变。不过，当我们放宽稳定的约束条件的时候，这个状态也能被视为稳定状态。

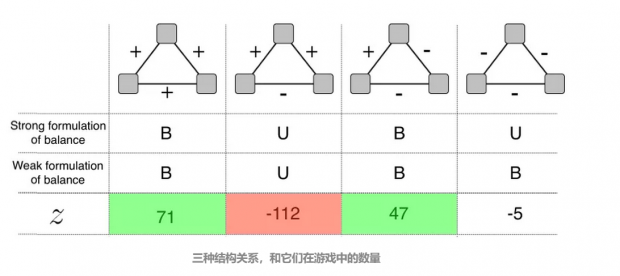
在这个游戏中，我们能够看到三种结构对应的数量，很明显“朋友的朋友是朋友”和“敌人的敌人就是朋友”这两种关系是非常稳定，不会发生转变，数量也很多。第二种“我的两个朋友是死对头”这种关系明显不稳定，存在的数量也非常的少，容易向其他的关系转变。而“三足鼎立”式的关系，虽然也不稳定，但相对而言并不显著。

研究发现，如果三人关系中存在“++”，那么新确立的关系是“+”的可能性比随机值要大 7 倍；如果三人关系中存在“+-”，那么新确立的关系是“-”的可能性比随机值要大 11 倍。

不同网络间互相影响

在网络中，我们也会看到一些符合传统社会准则的用户行为。比如说，当一个人做出了一个积极友好的行为，也很有可能收到一个积极友好的回应。反之，如果一个人做出了一个敌对行为，也很有可能被人敌对。

“投桃报李”、“以牙还牙”这样的行为都是存在的。甚至当一个人得到了消极敌对的反馈，更有可能再次被另外的人敌对——所谓的“墙倒众人推”。

从上面的结构稳定性分析中我们能够发现，友谊、敌对分别属于两种互动的网络，但这样的多层网络能够互相影响，即网络的影响不仅发生在同一属性的网络中，也会在不同的网络间传递。在本游戏中发现了几种网络间互相影响的现象：

通信-友谊：关系好的玩家交流更密切。

贸易-通信：做生意自然需要进行大量的通信，换句话说，进行了大量讨价还价通信的玩家也是有诚心的卖、买家。

敌对-攻击：彼此敌对的玩家会互相攻击。

敌对-赏金 / 赏金-攻击：与敌对-攻击类似，敌对势力会发布悬赏，自然也就有赏金猎人为了赏金而发动攻击行为。

通信-敌对：我们能发现即便是敌对的玩家之间也会存在通信。这一点与真实的社交网络非常类似，“彼此拉黑”的人与人之间其实也存在着“隔空喊话”的间接通信行为。

游戏网络中的幂律分布

幂律是一种在现实社会中非常常见的关系，从生物体的生长、城市的发展规模、公司的组织形式都能看到幂律关系的影子，在本文中所研究的游戏社交网络中也不例外。一下简述几项研究者发现的幂律关系。

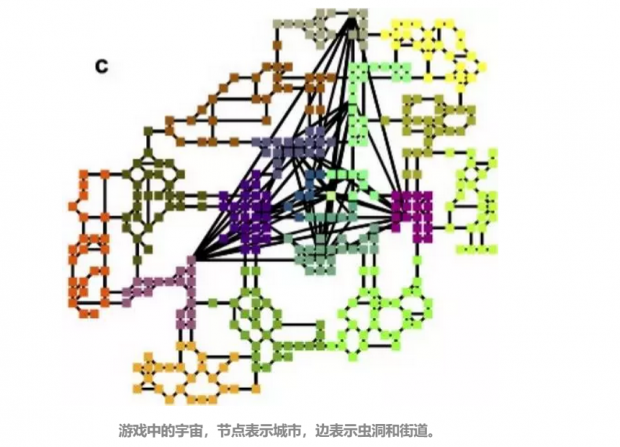
通信网络

在电话通信网络，电子邮件网络，甚至是在线上社交网络中的个体，他们的交互延时与抽象的“距离”（例如在本游戏中，距离就是游戏世界中的迁移需要的步数）分别呈现出了幂指数为 -0.83至2.0 的幂律关系。

参考我们熟知的万有引力：“距离越近，引力越大”。可以类比为在游戏中，两个玩家距离越近，互动越多，促使互动的吸引力也越强。但是也有例外就是“攻击”，当距离够近的时候攻击呈现出的是一种“斥力”。不过这一点很好理解，玩家跑来攻击对方玩家，但奉行“打一下就跑”，“打一枪换一个枪眼”的游击战术。

在满足三元闭包的网络中，度分布（ degree distribution）、依赖核心（attachment kernel）、聚集系数（ clustering coefficient）这些都能用相应的幂律函数表示出来。换句话说当相关幂律系数得以确定，我们就可以预测出网络未来的发展。

层级组织结构

在网络中，我们也会注意到一些层级组织结构，比如说，第 0 层代表玩家自己，第 1 层表示亲密的朋友，第 2 层表示泛泛之交，第 3 层表示联盟成员，等等，我们发现每一层的人数近似地服从幂指数为 4 的幂律关系。

在游戏中玩家要依靠“虫洞“进行跳跃，每次跳跃的距离和为了跳跃而等待的时间分别服从幂指数为 -3 和 -2.2 的幂律关系。

财富分布

我们或许都听说过“20% 的人拥有 80% 的财富”这样一个经验法则，确实在现实的社会中财富分布会遵循幂律分布，例如以福布斯杂志在 2003年10月，美国富人的净资产我们发现美国的财富分布遵循幂指数为 -2.1 的幂律，而在 Pardus 世界中这个规律同样存在，但幂指数是 -2.5。

性别行为差异

游戏中的几种角色图像，及其性别区分。

游戏为玩家提供了多种角色可供选择，每个角色都提供了男女两种性别。玩家可以自己选择游戏中的性别，值得注意的两点是：

在游戏中有接近 90% 的玩家设定为男性。

玩家在游戏中选择和自己生理性别相反的现象非常普遍。

这个行为被称为性别交换（gender swapping）。根据统计显示，在游戏中往往会有超过 10% 甚至 20% 的性别交换玩家。

根据来自本游戏的数据我们会发现，女性往往表现出风险厌恶，且更加的富有；男性因为更加好斗、承担更多的风险，因而死亡率较高。

不过如果不考虑破坏性的行为，男女间的差异不大。

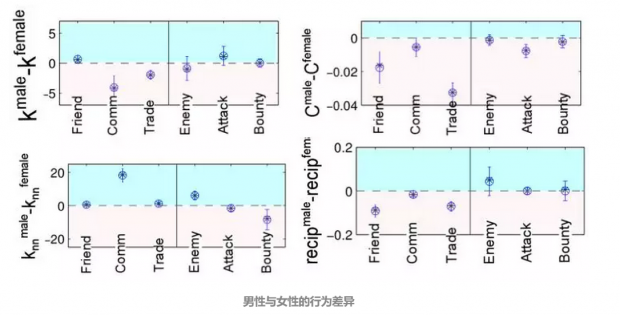
上图从友谊，通信，贸易，敌对，攻击，赏金六个网络来刻画男女的行为差异。纵坐标都是的是"男性减女性的差值"。这四张图分别表示的是：（a）平均的节点度数 k，（b）聚集系数 C，（c）邻里的平均度数，（d）互惠程度。

从图中我们能发现女性与同性间的联系更加密切，而男性则更喜欢和异性联系。

女-女间的交易和通信数量要明显的高于随机网络

男-女之间的交易和通信数量也非常高

女-男之间的类型行为特征不明显

男-男之间的交易和通信数量缺要显得少一些

同时，研究者发现女性会呈现出爱憎分明的情形；女性更爱抱团，有较好的“回粉”、“互fo”行为，也有更多可以聊天的小姐妹。而男性更喜欢去“结交社会名流”。在对待敌人的态度上男女也会有所区别，男性可能会直接攻击，而女性则会发出悬赏、赏金。

总体来说，

男性对女性的友好示意会做出快速的回馈，而对同性的示好反应比较慢；

女性对同性的友好示意会做出快速的回馈，对男性的示好则要反应的慢一些。

面对敌对行为，男性却对同性表示出快速的反馈，对女性则要温和许多了。

前沿展望

我们可以发现在 Pardus 这个虚拟世界中的社会现象与我们真实社会中的经验、理论、假说高度吻合。这能否意味着 Pardus 是一个好的社会科学模型呢？现在我们还无法得出结论，但也许在不久的将来，社会科学能够发展成为一门可以定量计算、可以预测的学科。孔德的理想也许能够实现。数据的规模和计算能力的约束都不再是社会科学的障碍——这些我们我们几乎都已经解决了。

也许有朝一日我们能够把 Pardus 的数据替换成真实世界中的数据，使得我们能更加深入地理解这个世界。

作者：Leo

编辑：王怡蔺

话题：