圣塔菲研究所外聘教授、密歇根大学复杂性研究中心主任斯科特·佩奇（Scott E Page）在Coursera上开设了一门名叫 Model Thinking 的课程。这门课以复杂系统的视角研究社会和经济学上的常见问题，介绍了十余个可以定量推演的模型。佩奇教授还出版了多本畅销书，例如《多样性红利》一书，佩奇教授创造性地提出：一个人是否聪明不是由智商决定的，而是取决于认知工具的多样性。

佩奇教授为他的课程撰写了一本厚厚的教科书 The Model Thinker，在2018年11月份出版。全书分为29章，每一章都干货满满。书中不止列出了更多的模型，还系统性地展示了如何使用多种模型来分析现实社会中的问题。

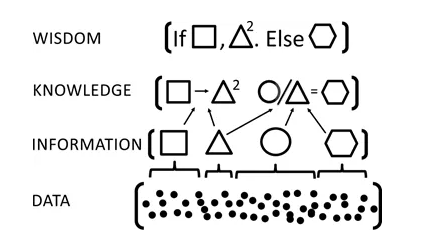
在从信息到智慧的每一步上，模型都可以成为上升的阶梯。整理数据、提取信息，你需要通过建模来去伪存真；根据不同领域的信息，最终得出一个对大局、新情况或未来的判断，你需要预测性的模型去产生知识；而要知道在何时何地该提取哪些知识，则需要通过模型让隐藏的假设显现出来。根据作者的总结，模型的7种作用包括推理、解释、设计、沟通、指导行动、预测未来和探究可能性。

类似的书还有《Algorithm to live by》。这本书讲的是用机器学习算法原理指导日程生活中的决策。关于如何决策，书中给出的回答是下图。

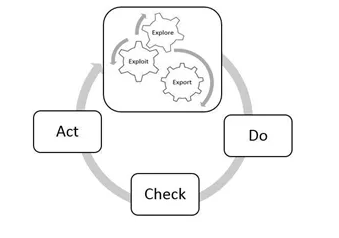
这个框架没问题，但由于日常生活中要解决的问题都与他人有关，而人是具有主观能动性的，人的复杂性和多样性决定了任何模型都需要对模型中的人予以简化，从而使得模型不会像和真实国土一样大的地图那样全面却无用。而对人的简化有多种不同的方式，从这个逻辑起点出发，可以推演出不同的模型。没有一个模型适用于所有的坏境，但多样化的模型可以带来1+1 > 2的效应。

模型学习

学习一个模型，要搞清楚其组成结构、生成逻辑与应用场合。

模型的组成结构除了实体和关系这些显式的部分，还包括模型对人和坏境做的假设。关于人的假设，包括：有绝对的理性及记忆力还是只能服从既定的规则、是否能够从过去的经验中学习、是否具有多个目标等。而关于环境的假设，包括：环境是否有多个属性、各个属性间是否相关、是否存在局部最优解、是否随着时间发生变化。

生成逻辑则是一串数学公式和推算，指出在模型给定的假设下，会出现怎样的结论。至于应用场景，一个模型可以在多个领域重复应用，一个模型也可嵌套进其他模型中，组成更大的模型，从而捕捉现实中更多的复杂性。

人群建模

关于人群的模型，首先要讨论是人的多样性。通过三种概率分布（normal，lognormal，power），可以对人群的多样性进行分类。三种分布对应着不同的假设，即不同时间点人获得的收益是否具有相关性，也包含着对环境的假设，即对人的评价取决于之前收益的加和或乘积。上述组合会产生上述的三种分布，以及一个长尾效应比幂律分布更显著的分布方式。

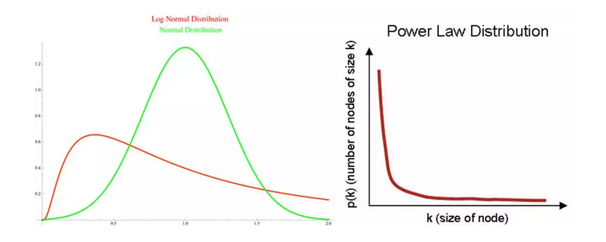
对人群的多样性进行了分类，可以判定人群大小对其结果的影响，例如假设学习成绩是服从正态分布的，那么一个学校越小，其平均成绩就越有可能超越全国的平均水平，这不是由于小学校容易培养出好学生，仅仅是统计上较大规模的学校普遍更靠近平均水平。

在考虑人与人的互动时，从个人的视角来看，可以根据外界对你决策反馈持续带来的收益（正、负、或者零）将模型分成三类。如果长远来看，外界没有对你的决策给予反馈，那你就可以使用线性模型去估计你决策的影响，可以通过P值来判断影响是否随机产生，可以通过R square来评估影响的大小。如果外界总是满足你，那正反馈就会带来不稳定。反观《黑镜》的剧情，其中不少悲剧是由于科技进步带来的心想事成。而负反馈则会带来稳定和均衡。

人不是在和一群人互动，而是在和一个个具体的人互动。将人看成个体，就可以组成网络模型或者网格模型。网格模型将人放置在一个一维或者二维的棋盘中，一个人只能和附近有限个人互动；最典型的网格模型是生命游戏（game of life）。

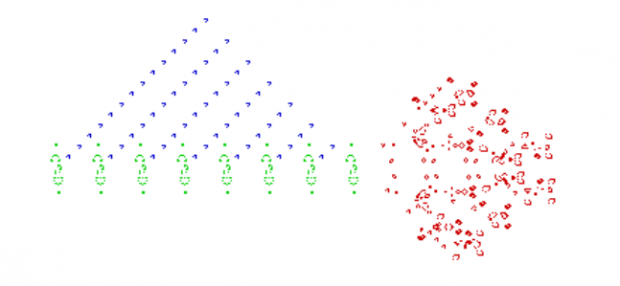
而网络模型则可以让人与人之间自由连接，例如人际社交、网页间的链接、论文间的引用。而如果人与人之间的互动有不同的类型，那就可以将做同一类的人抽象为一个整体，从而产生系统动态（system dynamic）模型，例如下图所示：

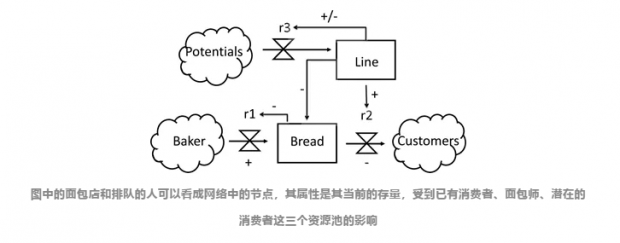
网络中的人不是孤立的，为了对其相互影响建模，可以先将人分成几类，通过互动，人的分类会发生改变。例如疾病或者想法的传播。为了引入人的不同，可以假定人有不同的阀值（threshold），只有影响足够强烈，才会被身边的人的影响。为了引入待传播的思想的多样性，可以将人的偏好分为spatial（离自己越近越好）和hedonic（越多越好），再结合上不同的网络结构，就可以针对网络上思想的传播按照不同的方式进行建模。

如果是为了预测，可以建立一个足够复杂的模型，但若是为了解释现象，或者探索未来的可能性，那就可以使用简单的模型，用足够简单的假设，让模型的推演重现出一部分直觉告诉你对的，再推翻一部分你本以为理所应当的结论。

人与人不是只互动一次的，马尔可夫链反映了不同次互动对个人的影响，而随机游走和路径依赖则可以看成是人与人持续互动所产生的模式的两个极端。互动的结果可能是合作，也可能相互的坑害，这其中就需要引入博弈论，引入经济学中的信号传递模型（cost signal），引入群体选择与名望来解释为什么合作是可能的。这其中有足够多的模型，几本书也讲不完，这里就只是蜻蜓点水的带过。

人与人之间的交往不止是个人行为，还涉及到制度的建立。例如如何在一个团体内分配成功的果实，如何决定集体的行动，如何协调不同的偏好。你可以先列出你的规则需要满足的条件，如同《几何原本》中的公理系统，这些条件要简单且符合常识，然后去判断能不能找到一个满足这样要求的制度。

有时你可以证明找不到满足全部条件的制度，那你就需要权衡到底要满足怎样的价值观，而有时则可以构建出来。例如夏普利值（Shapley Value），就是假设一个成员加入这个团体的顺序对其团队贡献度不应该有影响，因此对所有加入顺序下各个成员的贡献度进行加和平均。夏普利值可以用来解释为什么团队中有的人应该拿的多。虽然看起来有些人完成的成就不多，但是他们补足了团队的短板，例如下图的例子。

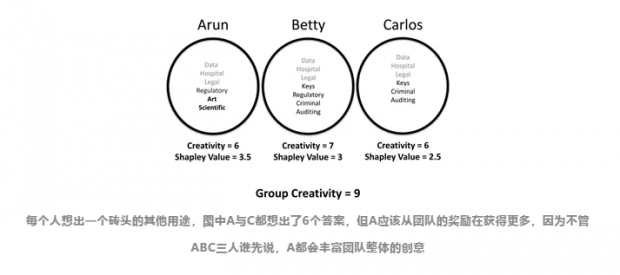
最关键的是，人是能够从错误中学习的。The Model Thinker 这本书的最后也是最难的三章围绕学习展开，先对比了强化学习和社交学习：前者根据之前的行动的收益来调整自己的认知，后者则根据他人的评价。不同的学习方式，可以导致囚徒困境中不同的纳什均衡在人群中成为主流。而当收益不固定时，多臂赌博机模型则能指出你该怎么平衡探索和收益。

这里较为细致的讲一个书中的例子 Gittins Index，算作这篇挂一漏万的读书笔记的收尾。感兴趣的同学可去修 Model Thinking 这门 Coursera课程，课程中涵盖了书中所讲的大部分模型。

Gittins Index说的是什么？

你有机会在接下来的回合获得1000单位的收益，90%的机会什么都得不到，请问你愿意为了这个抽奖的机会付出多少？

答案是假设你获得了抽奖的机会，你会在第一回合抽奖。第一次抽奖中了，那你就一直选这个；如果没抽中，那就选稳妥的，这样你的预期收益是0.1×1000+0.9×500，因此你愿意为这个抽奖机会付出550单位。Gittins Index 包含了贝叶斯的思维，考虑到了不确定性对未来决策的影响，通过一个计算公式，权衡了探索与利用（explore and exploit）。

在这本书的最后一章，书中用十余个模型解释了现实生活中的贫富差距为何越演越烈：有的模型专注于富人为何越来越富，有的模型解释了为何种族间的贫富差距越拉越大，还有的模型解释了为何寒门难出贵子。

模型思维的优势，不止体现在社会问题这样的经世济民中。对于年轻人来说，游戏中的模型思维更有趣。阅读这本书的时候，我一直在想书中的例子有哪些能够应用到杀人游戏中，例如马尔可夫链可以分析前后发言之间的关系，信息传播的模型可以预测投票的结果，如果能够写一本书，专门来讲如何在桌游中应用模型思维，那才真的有趣而有意义了！

作者：郭瑞东

编辑：杨清怡