导语

传统上对城市的研究主要从社会学、经济学等领域入手。而随着系统科学的发展和大数据技术的进展，研究者和决策者都可以获得大量的数据作为理论研究与规划建设的依据。

在2019年8月arxiv.org发布了一篇预印本综述论文中，研究者用分形几何学解释城市中的规模法则（scaling law）。本文通过解读这篇论文，介绍城市中的分形网络，并探讨城市标度律的成因。

 

城市的分形维度与幂律法则问题

 

城市或许是现代人类最伟大的发明，在大城市中聚集的人类，可以进行高密度的互动：交换思想、买卖商品货物、提供服务，等等。但维持这样高的密集程度本身也会成为负担：住房成本提高、交通通勤拥挤、污染对环境的破坏长期为人诟病。因此，政策制定者急需对城市的演变进行建模分析。从中找出城市发展的规律，并由此做出决策。

 

正如 Marc Barthelemy 在他的文章 The statistical physics of cities 中所言：传统上对城市的研究主要从社会学、经济学等领域入手。而随着系统科学的发展和大数据技术的进展，研究者和决策者都可以获得大量的数据作为理论研究与规划建设的依据。把城市结构视为一个分形网络；并结合大数据等技术赋予的数据资料和计算能力加以分析验证。从中分析出城市发展的一般规律。

 

从复杂系统到幂律成因

 

大多数研究者都认同，应当把城市看作一个复杂系统来进行研究，将参与其中的个人、机构以及政府部分视为基本个体。这些微观个体间的相互作用能在宏观上表现出不同的现象：人群的聚集、社会分隔、交通拥堵等现象。

 

在诸多的研究中，与城市有关的大量统计数据指标都与城市的扩张（人口增长）呈现出超线性或亚线性的幂律关系。并且这些幂指数存在一定的规律。这一现象在系统科学的研究中并不罕见，甚至可以说幂律是普遍存在的。

 

但也正因为如此，人们并不满足于从统计数据中“画”出幂律曲线、通过统计工具计算出幂指数的数，而是要分析出这背后的缘由。因此，幂律机制的成因，幂指数的现实含义，也是系统科学领域的一大研究重点。

 

这一点在城市复杂现象的研究中也不例外，当人们观测到城市的统计数据的幂律关系时，自然要分析这其中的原委。在来自 Complexity Science Hub Vienna 的 Carlos Molinero 和维也纳医科大学的 Stefan Thurner 的最新论文 How the geometry of cities explains urban scaling laws and determines their exponents 中。二位研究者也对城市复杂系统的幂律成因给出了他们的解释。

 

论文题目：

How the geometry of cities explains urban scaling laws and determines their exponents

论文地址：

https://arxiv.org/abs/1908.074701

 

城市中的分形网络

 

分形理论是系统科学研究者在研究幂律成因中常用的数学工具。圣塔菲研究所前所长、《规模：复杂世界的简单法则》的作者，杰弗里·韦斯特(Geoffrey West）的一项经典研究就是利用生物血管的分形结构来解释克莱伯定律（Kleiber's law）。在本研究中，研究者也试图利用城市的分形几何结构，去解释幂律的成因。

 

考虑到不同城市的地理方位、文化背景、形状差异，均存在很大的差异。分析城市的幂律法则这并不是一件简单的事情。研究者的一个基本想法就是，把城市的看作是由道路网络的分形几何体构成，这样就能在一个二维的平面上描绘出城市的形态。而人共同生活在城市的一个点上（共处一栋楼的不同层）则构成了城市的另一个维度。人在其中做进行的互动也就是城市中幂律法则超线性、亚线性规律的来源。

 

在本研究中，人口数据来自 Global Human Settlement (GHS) Population Grid；城市道路、城市建筑物高度数据来自 OSM 数据集；而 Eurostat 提供了每个城市的GDP数据。而研究者主要研究、验证的国家是：英法德西意五个欧洲国家。

 

 

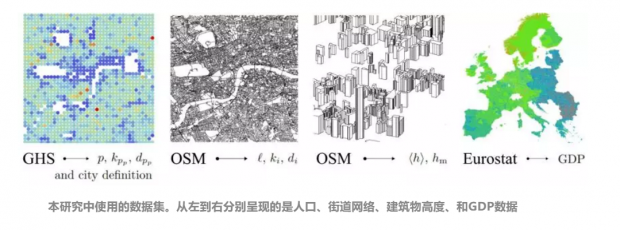
城市分形四步走

 

 

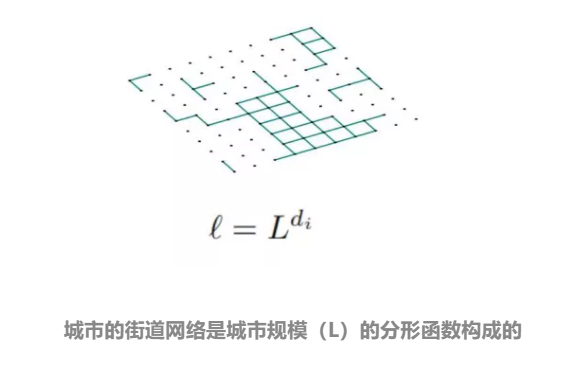
如上图所示，我们来考虑一个规模为 L 的城市，街道网络的分形维度介于 1~2 之间。可是，对于一个“有高度”的城市而言，二维平面的分析是不够的。人口所带来的分形维度就体现在了街道上的建筑物里。考虑到人口带来分形维度很难计算，研究者在这里先计算了一个分形维度的投影：

 

 

因为，建筑物是沿街道建立的，并且，人类也主要在建筑物中生活和工作。因此，研究者可以认为这个由人口带来的投影维度和街道的分形维度近似。

 

只是，人类的活动并不能被视为是“堆”在地面上进行，换句话说，要考虑到建筑物的高度所带来的维度增加。如果假设所有的建筑物高度都相同，人口的分形维数应该是投影维度加一。那么城市这样表示：

 

 

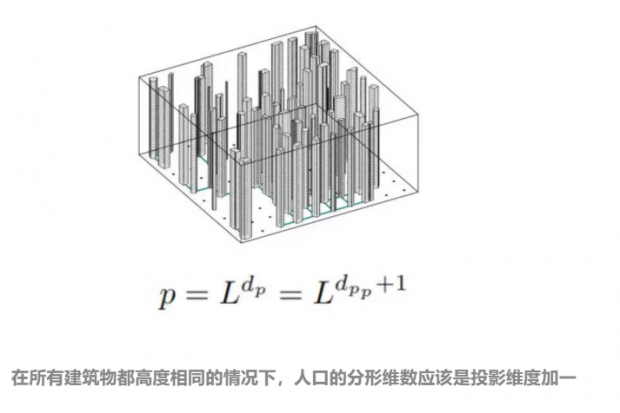
但如果我们考虑到建筑物的维度并不一致，则意味着分形的维度要这样表示：

 

 

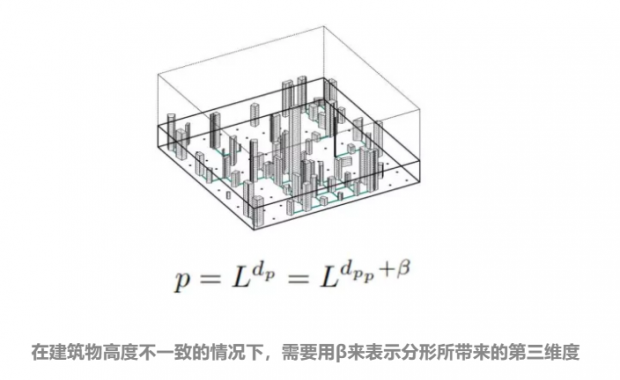
在这样的分析中，我们可以看到，最终，由于城市的高度维度（β）是一个小于 1 的数。故此，所对应的人口分形维度要小于 3的数。也就是说，考虑到建筑物高度的差异，人类并不能从地面开始“堆”满整个三维空间。

 

稳定的幂律法则

 

通过上面的建模分析过程，以及数学形式化的推导计算。研究者认为，城市幂律中的亚线性幂指数（γ_sub）等于道路分型维度和人口分形维度的比值。正如前面分析的，道路分型维度介于1~2之间，人口分形维度比道路分型维度大。自然，这个幂指数是一个小于1的数。

 

 

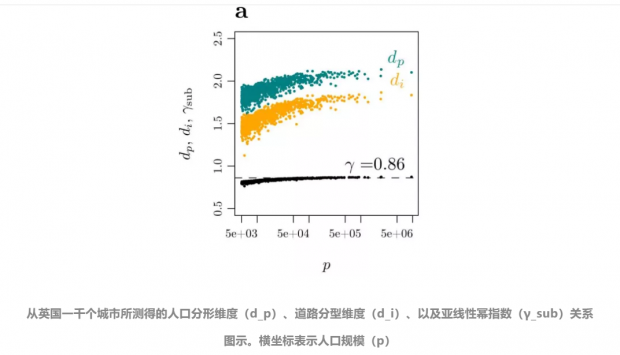
从上面的“人口-人口分形维度、道路分型维度、以及亚线性幂指数”图像中我们可以看出一点：分形维度并不是一个固定的数值，而是随人口规模变化的。但是，城市的幂指数却接近一个稳定的常数 0.86。

 

为了能进一步的确定这种关系，假定一个单位大小的空间，在这个人类的最多互动次数接近于期望人口的平方，幂指数为2。

 

研究者确认，在城市的幂律法则中，超线性幂指数（γ_sup）+亚线性幂指数（γ_sub）=2。

 

 

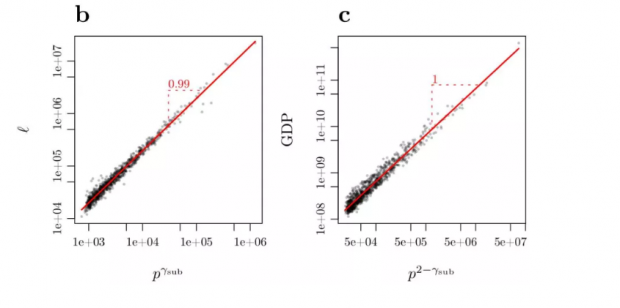
通过实验数据，我们看到城市道路长度（左图）与城市的GDP（右图）所分别呈现出的亚线性与超线性规律。（体现在横坐标上）。

 

城市的密集和高度

 

研究者为也为城市建筑的高度提供了一个直观的解释：城市的人口数量与城市街道的长度之比。同城市的人口相比，服从（1-亚线性幂指数）的幂律关系。

 

 

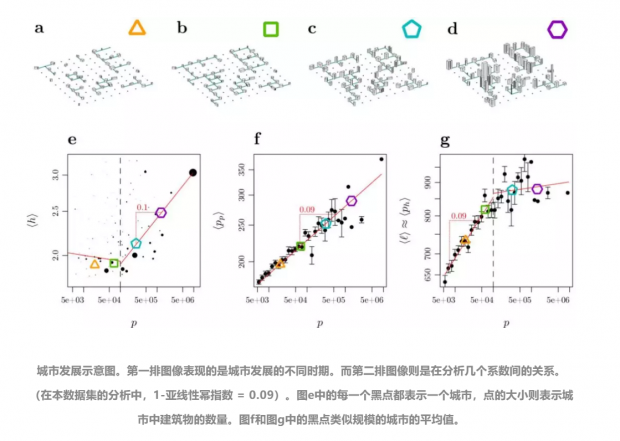
在上图中，我们可以从第一排的图像中发现城市的发展并不是直接平地起高楼的，而是会先在水平层面上扩张、变密（图a、b）。但是，当人口的数量过了一个临界阈值时，才会兴盖高楼大厦。（图c、d）。这一点在图e中得以体现，垂直的黑色虚线就表示 100,000 人口阈值。不过即便超过了阈值，斜率也仅为0.1。图f表面，人口在水平层面的投影数量和实际人口数量相比也符合 0.09 的幂律关系。而图g则是在描述每一个楼层的人口密度和实际人口数量的关系。我们能够看到在 100,000 人口阈值一下时，每一楼层的人口增长符合 0.09 的幂律关系。而当超过这一阈值以后，每一楼层的人口密度则接近饱和。

 

总结

 

城市的幂律法则深刻的影响在在城市中生活的每一个人。从分形几何的角度来看待城市，研究者为我们找到了一条解释城市幂律法则的一个新途径。同时，研究者也表明这样的幂律法则规律在不同人口规模的城市中是稳定存在的。也就意味着城市——这台不断加速的跑步机——会为我们的生活注入源源不断的活力。

 

作者：Leo

审校：李睿琪

编辑：张爽