Nature Communication：人群移动行为新视角——矢量场模型-集智俱乐部的财新博客-财新网

导语

人口如何迁徙？病毒怎样传播？交通为何拥堵？为群体移动建立合适的模型是解决这一系列问题的关键。传统的引力模型、辐射模型等已有良好效果，而在近期发表在Nature Communication的一项工作中，研究者提出了“矢量场模型”，基于从社交网络中捕获的通勤数据，用“场”来描述人群在不同位置的移动方向和流量。新模型取得良好的效果，开拓了群体移动问题的研究思路。

人类行为的复杂性是当今复杂系统研究的热点之一，其中预测人类空间移动行为更是人类行为复杂性研究的核心课题。无论是城市交通的设计和规划，还是传染病的演化和传播，或是理解社会网络的形成机制等，都与人类空间移动行为有关。

在2019年8月发表于 Nature Communication 一篇论文中，作者根据日常通勤数据，创新性地提出了一种群体移动的模型。这不仅为人类空间移动行为提供的新的研究视角，也为解决城市功能分区的定义以及城市多中心存在性等问题提供了强有力的工具。

论文题目：

Field theory for recurrent mobility

论文地址：

https://www.nature.com/articles/s41467-019-11841-2

1.人群移动行为的三个经典模型

实际上，在过去的几十年里，对于群体的空间移动问题已经存在一些经典模型，它们都为人类群体移动性问题建模提供了重要的数学框架。

群体移动模型中主要存在两种思想流派：第一类是引力模型(gravity model),顾名思义，与牛顿万有引力定律相似，距离越近，引力越大，距离越远，引力越小。模型基本假设是两个地点之间的旅行次数是其物理距离的递减函数。

第二类是基于经济学的介入机会模型（intervening opportunities model）。人从一个地点迁移到另一个地点，不仅受到两个地点之间规模和距离的影响，而且受到两个地区的中间地带的影响。迁移对个人来说是很耗费资源的，所以如果在中间地带找到合适机会，就会停止继续找别的机会。这里“介入机会”即两个地点间中间地点的就业、居住机会，介入机会的多少和分布情况，决定了人口在两个地点之间的流动性。

由于分布在空间上的机会可能是高度不均匀的，因此与引力模型不同，在介入机会模型中，物理距离对最终分行目的地起着间接作用，进而对流人类移总流量的衰减也起着间接作用。

2012年，“介入机会”的概念进一步被推广到物理学中的粒子辐射过程，引入了辐射模型（radiation model），借鉴了物理学中的辐射过程，假设出行者会选择距离起点最近的一个地点。与引力模型不同，辐射模型是无参数模型，因此简化了建模中调参的过程，但同时也减弱了模型对某些现实情形的描述。

如今，随着大数据时代的到来，人获取类的空间移动信息不的方式发生了变化。研究人员再主要依靠观察访问、调查问卷以及出行日志等方式获取，借助无线通讯、在线社交网站等获取海量的更、高时空精度的人类移动轨迹信息。这些都为群体移动行为的定量化描述提供了有力的撑，为人类的空间移动问题研究带来了新的机会。

在今天我们介绍的这篇文章中，作者便借助Twitter及人口普查数据中城市人口的工作地和居住地信息，引入了矢量场模型。其实，通常情况下，矢量场常常用于描绘流体的流动，那么现在对于人流这样的群体移动同样引入矢量场描绘会对群体移动问题本身带来怎样的线索呢？文章中给了我们一些解答。

2.定义矢量场：如何用通勤数据刻画群体移动

首先，我们先看看何为矢量场？简单点，就是由矢量（向量）构成的场。例如，常见的电磁场，速度场等等。那么何为矢量呢？即同时描绘大小和方向的量。有了这些说明，我们对人群移动对应的矢量场似乎也并没有清晰的概念。

研究者把每天上下班，在 i 和 j 之间的通勤者，称为Tij，通勤者在各个方向上（不同的 j），都有有一定的流动可能性。从工作地i到某个居住地 j 的人口流动，都是一个以 i 为中心，以从 i 到 j 为方向，以i和 j 间距为模长的矢量。对以 i 为起点的这些流动矢量求和，得到Ti，它表示 i 点人群移动的矢量。

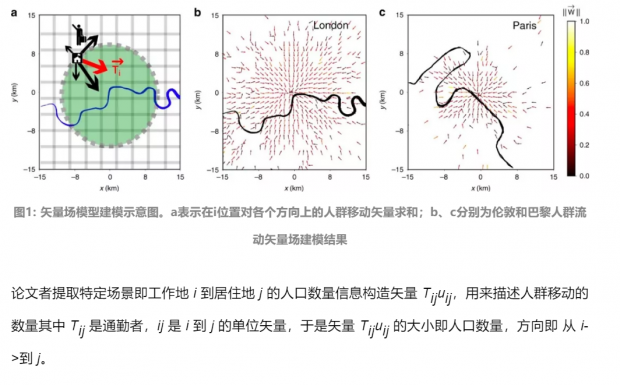
3.人群矢量场的特性：流量之差等于存量

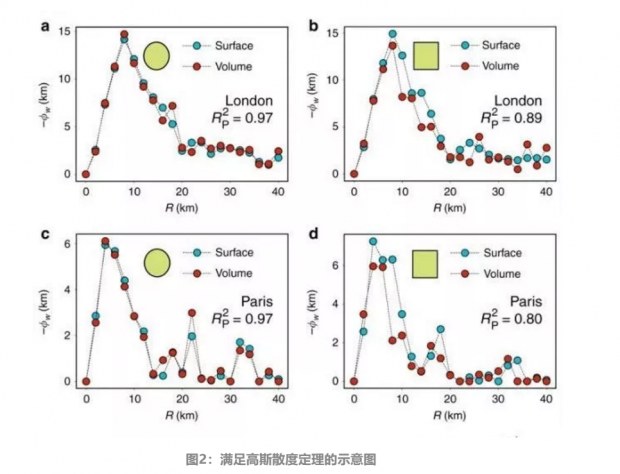
什么是高斯散度定理？高斯散度定理是分析矢量场的重要工具。从数学上解释，即矢量场穿过曲面的通量，等于散度在曲面包围体积上的积分。具体到人群移动的模型中，依据工作地到居住地的人群移动数据，高斯散度定理可以直观地理解为一种流量关系——

进入某区域上班的所有人数减去已经下班回家的人数，等于某个区域中的现有的人数。可以通过进入和离开的流量来估算区域中实际的人数。文中作者根据Twitter数据计算多个城市对应矢量场W的面积分（矢量穿过边界曲面的通量）和体积分（散度在曲面所包围体积的积分），发现城市的矢量场都很好地满足了高斯散度定理。

4.矢量场的无旋性

另外，与通常矢量场分析类似，讨论了矢量场 W 的散度后，作者也计算了矢量场 W 的旋度，并说明 W 可以考虑为无旋场。

那么什么是旋度呢？顾名思义，就是矢量场中对旋转的衡量。直观点，我们可以想象图3的矢量场中有一个“旋涡”，旋度即衡量这个“旋涡”旋转的强度。显然，我们很难想象依据工作地到居住地的通勤数据建立的矢量场 W 中会存在这样的“旋涡”。

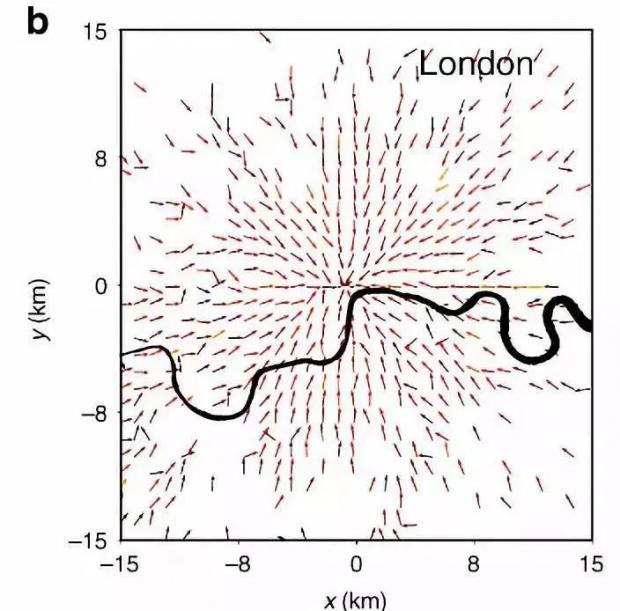
图3：人群移动矢量场是无旋场，图为伦敦的矢量场

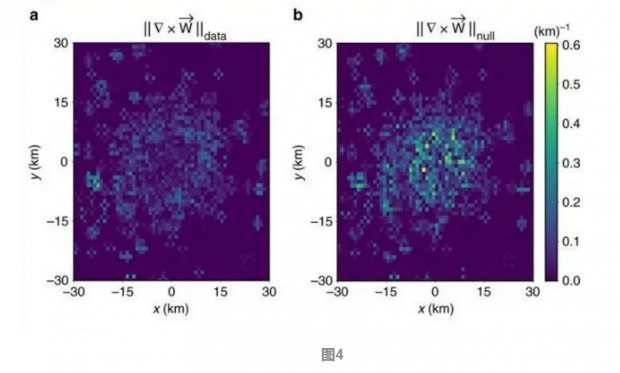
用图4作为论据之一也向我们说明了 W 的无旋性，其中图4a以伦敦为例，向我们展示了该城市通勤流定义的矢量场的旋度，可以看到，旋度的值约为10^-1km^-1；为了让我们能够对计算的旋度值有一个定性的认知，作者将图4b作为对比，向我们展示了随机重定义每个位置点的方向的模型的旋度值，可以看到，矢量场 W 的旋度与随机重定义的模型旋度值相匹配。另外，文中还对更多城市相关量进行了计算，所有这些证据都支持矢量场 W 的无旋性。

5.矢量场的势：位置间的势差决定流量方向与强度

至此，我们可以对无旋矢量场W 进一步通过公式W=−∇V定义一个标量势，从而可以在更低维的系统上编码人群移动信息：将每个位置点的矢量问题转化为标量问题，位置点间的势差即决定了流动的方向和强度。

“降维”一定程度上降低了问题的复杂性，并且可以利用标量势作为城市（多）中心定义的基本工具；另外势的形状也揭示了城市流动的空间组织，类似于地形图的等高线，我们可以将城市按照某一固定百分比从势最大值位置处依次划分作为城市分区的依据等。

这在规划基础设施和公共服务时，都具有重要的实际意义。如图5a,5d即以伦敦和巴黎为例展示了相应通勤流矢量场的势。显然，市中心的人口密度最高，势的值也最大；而势的最小值处即为人群迁移的平衡点位置。

实际上，在前文已经提到的引力模型引入后不久，人们就讨论了确定势能的可能性，但由于当时缺乏可靠的数据，这方面的进一步研究无法进行。

于是，借助于Twitter通勤数据信息，作者不仅计算了矢量场 W 的势，也将其与经典的引力模型的势做了对比：图5b，5e展现了相应引力模型下势的信息，明显可以看到，即使前者存在一定小范围的波动，两类模型的势总体特征是一致的，图5c，5f中也精确地展示了两类模型的相似性。进一步地，图6为我们展示了其他几个城市的Twitter数据获得的通勤流量计算的等势曲线。

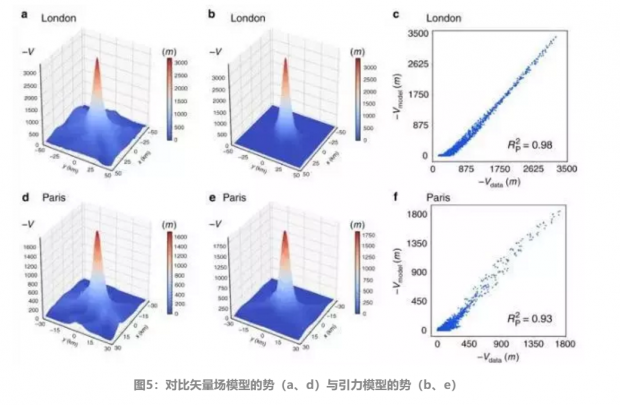
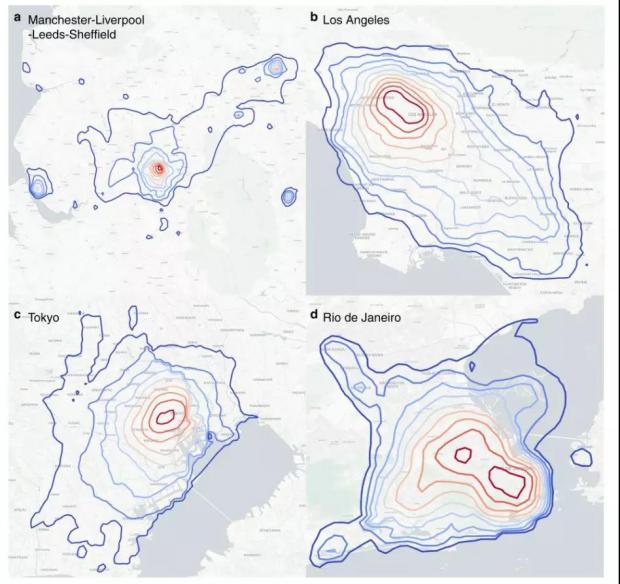
图6：根据Twitter通勤数据推算出来的城市通勤流量等势图

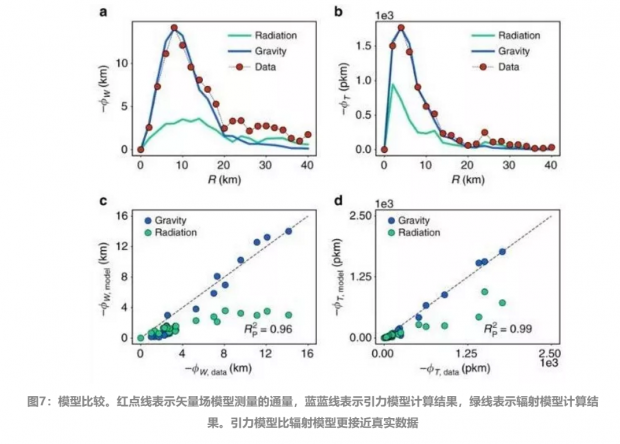
当然，除引力模型外，前文也提到群体流动模型研究中的辐射模型。文中也引入辐射模型进行了对比分析：图7a，7b可以明显看到，相较于辐射模型的结果（绿线），引力模型预测的通量（蓝线）能够更好地匹配由实证数据定义矢量场的通量（红色点线），而从图7c，7d也可以看出，引力模型和实证数据矢量场通量有很高的相似度，而辐射模型的结果明显偏离。这是由于引力模型更好地再现了实证数据群体流动的方向，于是矢量场模型也为探索各模型的性能提供了相关的依据。

6.结语

在这篇文章中，我们了解了一种新的模型——矢量场模型可以用来分析人类群体空间移动问题。然而，人类移动性这样的复杂问题其实还存在诸多挑战。大数据为这样研究带来了新的契机，同时也隐含了很多需要处理的问题。

例如，海量的数据是否存在偏斜，如何利用现在的数据挖掘，机器学习等方法从中提取有用的数据信息，还有待进一步发掘。

另外，人类移动性问题是涉及诸如统计学，计算机，复杂网络等多学科交叉的问题，我们在研究人类群体移动特征时，也应该充分结合问题的实际背景，这样才能更深入地为了解群体行为特性，从而更好地应用于实际场景中。

作者：步时

编辑：荣玉琪

话题：