导语

 

随着网络神经科学的发展，网络模型的建构日渐走向多元化，但模型应用的差异性也使沟通变得困难，为科研合作带来了障碍。因此，寻找更好的网络神经科学模型分类方法成为了当下亟待解决的难题。

 

本文检验了网络神经科学领域中模型的使用情况，提出一种基于三个维度的网络模型分类方法，并分析了对于模型效度的检验目标。本论文主要作者 Danielle Smith Bassett 是一位物理学家与系统神经学家，任教于 University of Pennsylvania， 研究方向主要为通过结合网络科学的方法理解人脑的学习，以及其他的复杂物理和生物系统。

 

论文题目：

On the nature and use of models in network neuroscience

论文地址：

https://www.nature.com/articles/s41583-018-0038-8

 

网络神经科学

 

一个多世纪以前，卡米洛·高尔基（Camillo Golgi）将切成块的脑组织浸泡在硝酸银溶液中，为错综复杂的神经细胞形态，取得了最早也是最详细的观测记录。

 

在这项技术的基础上，拥有艺术家才华的神经科学家圣地亚哥·拉蒙·卡哈尔（Santiago Ramon y Cajal）绘制了精细的神经元画像，这些画像向人们揭示了神经元的独特之处——每一个神经元细胞在解剖学意义上都可以看作一个独立单元，单元与单元之间有无数复杂的联系。

 

这种“神经元为基本单位”的思想被称为神经元学说（The neuron doctrine)。这一学说，对于现代神经科学在神经系统结构及功能上的理解和研究，都有深远的影响，也为网络神经科学的发展打下了基础。

 

网络神经科学的研究对象，主要是结构错综复杂的大脑。这个学科使用物理等其他领域所开发的工具来研究基于神经现实的网络系统模型，这些系统能被定义为独立功能单元与它们之间的关系，其中单元称为“节点”，节点间的连接称为“边”。开发并分析网络模型，能帮助我们理解这些模型代表的真实神经网络，并对其机制进行解释和预测。

 

用于神经系统的网络模型中，最简单常见的就是以神经单元为节点，表示它们之间的边的简单图。在此基础上，可以为边添加权重，为节点添加值，或是显性的函数来表现其动力学特征。

 

一个简单图可以再次概括抽象，成为单条边可以连接任意个节点的超图，或是新单元由多个基本单元组成的单纯复形。多层网络可以用来表示彼此相连的多个网络集，动态网络可以用来表示网络系统形态随时间的变化。

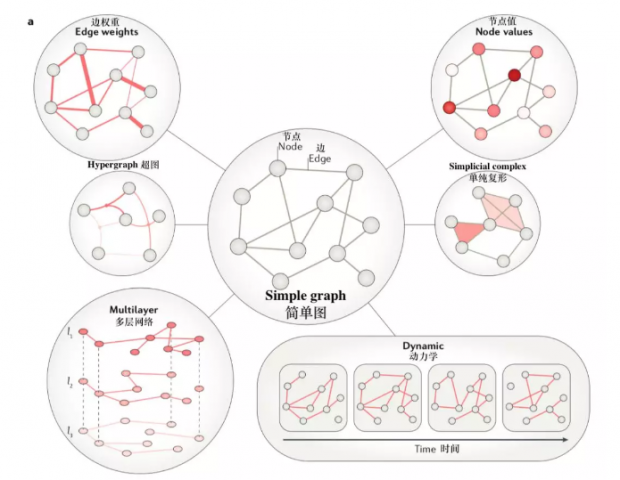
网络模型支持许多量化分析的方法。最常见的，就是通过 N x N 邻接矩阵 （adjacency matrix）进行成对比较（pair-wise comparison）。邻接矩阵的结构，能够进一步用一套叫做图论（graph theory）的数学方法进行描述与推导。除此之外，也可以对于简单图进行抽象概括后再分析（如超图或单纯复形），或使用不依靠图论的分析方法。

 

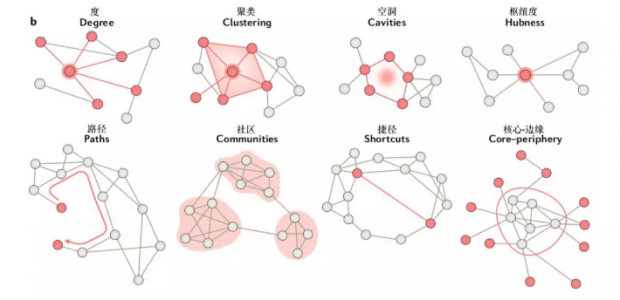
下图展示了一些网络神经科学模型中常用的测量方法：

 

度（degree）：从一个给定节点出发的边的数量

 

聚类（clustering）：节点聚类的倾向，计量上与边组成的三角结构的数量相关

 

空洞（cavities）：节点之间没有连接，信息不能直接流通的局部区域

 

枢纽度（hubness）：节点对其他节点的影响

 

路径（paths）：可供信息传输的路径

 

社区（communities）：局部密集互联的节点组

 

捷径（shortcuts）：让信息更直接地传输于部分节点间的边，或能标识较高的全局信息传输效率

 

核心-边缘结构（core-peripheral structure）：一种网络结构，对于稀疏连接的区域之间来往的信息，可更有效地进行局部整合。

除了以神经元为单位，网络模型也可以建立于许多其他的角度和层面。

 

一个网络中描述的系统，在空间尺度上可以小到描述一系列的染色质，也可以大到包含多个类器官，或多块皮质切片。网络中的节点可以描述解剖意义上的单元，例如细胞，也可以描述功能意义上的单元，例如基于功能激活定义区分的脑区。同理，边也可以描述物理存在的元素，例如突触、白质，或相对抽象的元素，例如距离、结构协方差、统计学相似性等。

 

网络模型的建构，早已不再限于卡哈尔在显微镜下看到的神经元网络，而是趋于多元化。虽然都叫做网络模型，不同的学者对于自己的应用可能作出不同的假设，引向不同的分析和结论。

 

应用多样化本是件好事，但模型应用的差异性也使沟通变得困难，为科研合作带来了障碍。若要促进科学发现，网络神经科学需要更好的模型分类方法。本篇文章检验了网络神经科学领域中模型的使用情况，提出了一种基于三个维度的网络模型分类方法，并分析了对于模型效度的检验目标。

 

基于三个维度的网络模型分类法

 

本文提出，网络神经科学中所用到的模型种类，可以按照三个维度来进行分类。第一个维度由数据表征延伸到理论构建，第二个维度由功能现象延伸到结构层面，第三个维度由粗颗粒度延伸到基本单元。

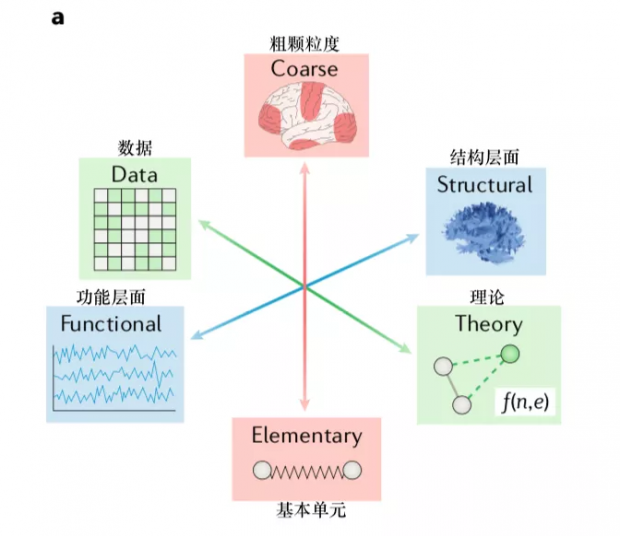
维度一：从单纯数据表征到第一性原理（First-principle Theory）构建

 

第一个维度由数据表征延伸到理论构建。

 

这个维度关注的问题为：该模型是否只是对于观测到的数据的直接表征，还是对于数据背后的系统运作机制提出了理论？

 

从数学的角度来说，一个数据表征的模型一般以图的方式呈现，例如简单图、时序图、多层图，有注释的图等。

 

最早应用数据表征的模型便是卡哈尔与其学派传人。例如，一个包含猕猴中多个视觉相关脑区的模型，整合了大量已发表数据，表明这些脑区间的连接符合分布式结构的信息处理模式。类似的相关研究，分辨了中央与周围脑区在感官处理中扮演的不同角色。随着图算法的普及，神经系统连接组学研究目前从秀丽隐杆线虫到人类，从宏观到微观，都有许多成果。

 

但数据表征的模型对于其观测的系统难以作出解释和预测，系统的机制怎么形成、接下来会发生什么变化，都无法直接回答。

 

这些预测和解释能力，正是第一性原理模型的强项。

 

在数学上，基于理论的模型必须将图与一个描述系统机制的差分或微分方程结合起来，其描述的机制可以是动力学，进化过程，或节点与边的功能等。最常见的做法是对网络图里的每一个节点都加上一个动力学模型。在微观层面，相关的动力学模型包括 Hodgkin–Huxley，Izhikevich，和 Rulkov Map。对于神经元集合，常见模型包括FitzHugh–Nagumo，Hindmarsh–Rose 和 Kuramoto Oscillators。对于更大的组织，神经质量模型被用来研究神经同步、可塑性、及神经疾病等现象背后的机制。除此之外，有的网络控制理论模型研究特定网络中，外来输入如何影响神经系统的网络动态。最后，虽然相对少见，也有些模型定义边的动力学，例如生成网络模型。

 

总的来说，数据驱动的网络模型能更大程度地保证模型的生物现实，但若要检验关于系统机制或动态学的科学假设，基于理论的模型会更合适。处于该维度中间的模型，则尝试结合维度两端的优点，通过数据驱动的方式定义理论，例如在动力学模型中使用基于数据推算的参数。

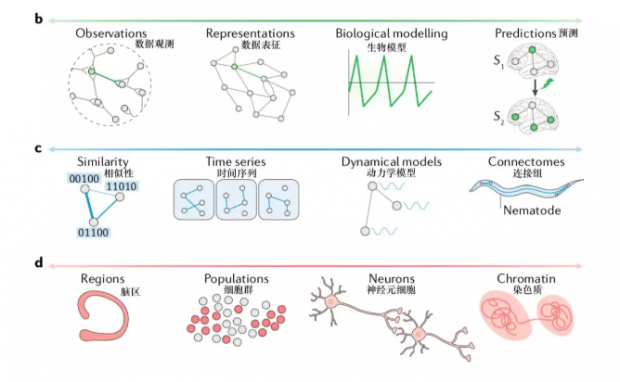
维度二：从生物物理现实（bio-physical realism）到功能现象（functional phenomenoloy）

 

第二个维度由生物物理现实延伸到功能现象学。

 

生物物理现实主义的网络模型包含物理存在的现实元素，例如以神经元作为节点，以神经轴突连接模式作为边。就算要包含动力学元素，也完全基于生物现实，例如对于神经形态发展或再生的准确描述。相对而言，处于功能现象学一端的网络模型中的节点和边，不一定对应真实物理存在。这些模型中可能包含人脑影像学数据中的功能连接性，或是细胞神经科学中的噪声相关性。其包含的动力学元素，则可能是在抽象层面描述了某观测现象的网络进化原则。

 

最典型的生物物理现实网络模型，大概就是秀丽隐杆线虫结构连接组模型了。这个模型里，节点是神经元，边是化学突触或电突触。在更大的空间尺度上，有小鼠，猕猴与人类的大脑结构连接组的模型，以白质束作为边，以它们连接的组织作为节点。

 

生物物理现实网络模型不仅可以基于数据表征，也可以基于理论原理构建。例如，网络控制的简单理论已应用到包含白质束的模型中，长距离协调的复杂理论则已应用于振荡皮层回路模型。

 

功能现象学网络模型中的边，则往往是在一个节点时间序列中，通过功能连接性或者统计相似性等度量来定义的。

 

功能性的边表示的不是物理意义，而是信息意义，例如节点间的同步，锁相，相干性和相关性等；这些边常会与对应确切物理体积和位置的节点结合考虑，以得到细胞或脑区层面上的功能性网络模型。这些网络模型中的节点，也可以非物理现实的原则来定义，例如在时间序列内释放的电信号在统计学上的差异。

 

功能现象学模型也可以与明确的动力学原理结合，例如在结构连接组中研究中，受到互联网排队论启发的信息传输分组互换模型。这些研究倾向于将大脑理解为一种信息处理系统，而不是其特定的物理实现。

 

描述生物物理现实的模型，能够整合大量实验观测数据并保证物理真实性，但存在计算量大、难以阐释解读的问题。描述功能现象的模型，能够更好地捕捉大脑信息处理的过程，但难以直接与神经结构联系起来。处于这个维度中间位置的模型，可能的优势，在于能够通过节点间基于现实机制测量的连接性，估算其功能性的交互。

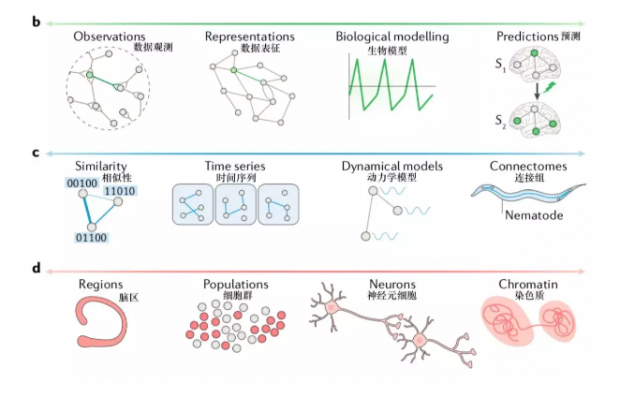
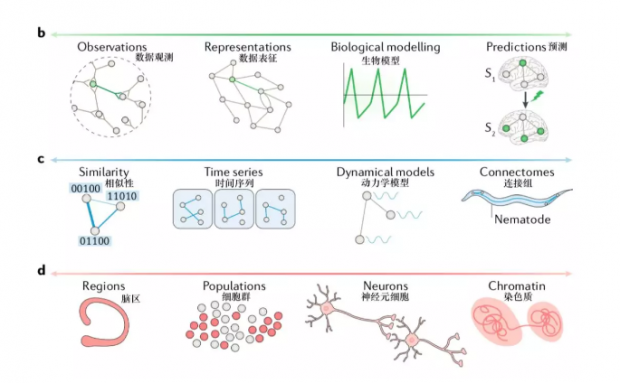
维度三：从基本描述（elementary description）到粗颗粒度近似（coarse-grained approximations）

 

第三个维度由基本描述延伸到粗颗粒度近似。

 

在网络神经科学的背景下，基于神经元学说，基本描述通常指神经元层面或以下，而粗颗粒度近似则指以上的层面。

 

基本描述模型中，节点和边是以自然基本形式存在、不可还原的元素，用于研究结构和功能之间的关系如何从这些基本描述中浮现。而粗颗粒度近似模型中的节点和边，则可能是相对而言更加高层抽象的存在，研究方向更加注重于理解网络系统中浮现出的特性本身，不一定需要明确地考虑系统的基本构造。

 

许多常见的网络模型都构建于神经元学说中的基本单元与关系，也就是神经元和突触连接。这些模型可以是数据表征，也可以是第一性原理；可以包含生物物理现实，也可以着重解释功能与现象。这些细胞层面的网络模型可以用于探索许多问题，例如神经生长、发展的机制。一些研究甚至已将这类模型扩展到了更小的尺度，在分子层面研究细胞内部的特定部分，例如神经突触的生长。目前还有研究正在试图在更基本的层面使用此类模型，研究神经元细胞发育过程中细胞核内染色质折叠所组成的网络结构。

 

粗颗粒度模型的构建，则是基于对较小单元组成的集合的简化描述。

 

物理学中常见的一个简化的例子，是在连续谱或平均场论中，将一个集合中有不同动力学的单元，模拟为一个节点，其动力学是所有原有单元的均值。粗颗粒度模型，常用于分子动力学、细胞生物学和生态学的模拟。

 

在针对大脑的研究中，它也被用于理解神经元放电活动与神经元集合之间的相关性。大规模的大脑网络模型也免不了成为粗颗粒度模型，例如神经影像数据，因为这些模型中想要包含的较小单元属性通常无法直接测量，所以每个节点的属性都是较小单元的粗略近似。

 

基本描述模型对于了解神经编码和细胞层面的网络功能最有帮助，而粗颗粒度近似模型则对理解总体结构编码与更高层面的结构功能最有帮助。这个维度模型当前的研究焦点，是如何开发能跨越不同规模层面的数据与理论的模型，尤其是通过分析理解一个层面的结构和功能，来推理和预测另一个层面的结构和功能。

当前研究在三维空间中的分布

 

本文认为上述的三个维度是相对独立的。

 

例如，一个数据驱动的模型，可以具有生物物理现实的结构，也可以更偏重功能现象描述；可以是细颗粒度、包含基本单元，也可以是粗颗粒度近似。

 

这些维度组成一个三维空间，网络神经科学领域用到的多种多样的模型，都可以在这个空间中找到自己的位置。

 

很大程度上，网络神经科学始于在较高层面上对于结构连接性的观察，使用图网络的表征，但没有任何显性的动力学描述。这一早期的方向仍保留了下来，在数据表征、生物物理现实以及粗颗粒度的近似方向有更多发展。相比之下，第一性原理理论、功能现象、基本描述的方向发展相对缓慢。在这个多维数据集中相关研究最少，就是基本描述层面上着重功能现象学的第一原理理论模型。

 

如何对于模型效度进行分析？

 

对于一个特定网络模型的效度进行评估，一般都是使用标准的统计模型选择方法。这些方法能在数据拟合优度和模型复杂度之间找到一个平衡，避免过度拟合，并提供简洁、可概括的结论。

 

然而，由于网络模型的用途多种多样，这个平衡或许非常难找，而且对于不同模型来说可能不太一样。例如，与解剖学意义上的连接模式的相似度，对于生物物理现实模型来说或许是合适的评判标准，但对于偏重功能、更加抽象的模型来说就不大合适。

 

基于研究精神疾病的动物模型效度评估方法论，本文根据不同的目标和领域，提出了一个对于效度评估方法的分类系统，包含了描述性、解释性、和预测性效度。

 

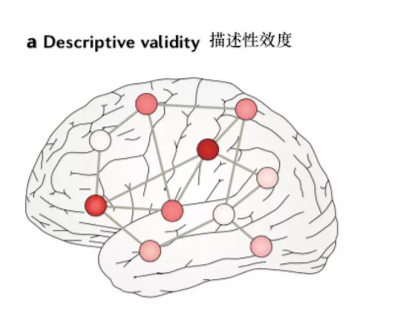
描述性效度关注的问题，是一个模型是否捕捉到了它模拟的系统中的关键特征，并与其足够相似。对于网络模型来说，描述性效度在于一个网络中节点和边组成的模式与它们所要表征的结构或功能数据是否匹配。下图展示了一个网络功能结构与物理现实相对匹配的模型，它便具有描述性效度。

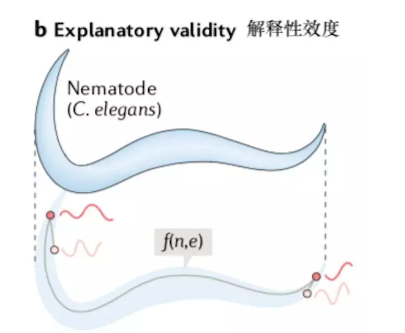
解释性效度关注的是模型理论构建，包括其支持怎样的统计验证与结论推断。一个具有解释性效度的网络模型，需要有真实大脑数据支撑其建构合理性，并且需要能基于其架构来测试网络系统中动力学或行为的因果关系。下图中，我们展示了一个可以用于测试真实系统（上）动力学间因果关系的描述网络节点动态的模型（下）。这样的模型，可以说具有解释性效度。

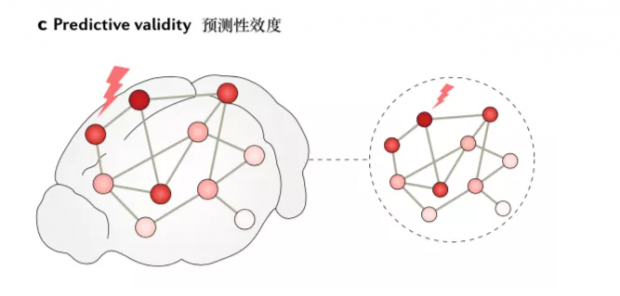
预测性效度关注的是在面对某种外界干扰时，实际研究对象与为其构建的模型作出的反应是否具有相关性。外界干扰可以通过药品，电或化学刺激，神经反馈机制，或是训练过程。在下图中，我们展示了一个模型对外界干扰产生的反应（圆圈内）和实际研究对象的反应（主图）相吻合的情况。这个模型可以说是具有预测性效度。

未来展望

 

由于模型数量与种类众多，不同模型能带来的合理见解也大不相同。

 

在实践上，研究人员必须明确地说明其研究目标，并解释所选择的模型与参数对该目标来说为什么合适、是否能够有效地测量其效度。另一方面，研究人员也可以构建跨越不同类型和维度的模型，或是以克服原有模型的局限性，并发扬不同模型的优势。

 

有很多方法可以帮助我们融合不同的模型种类。其中一种比较自然的方式如下：

 

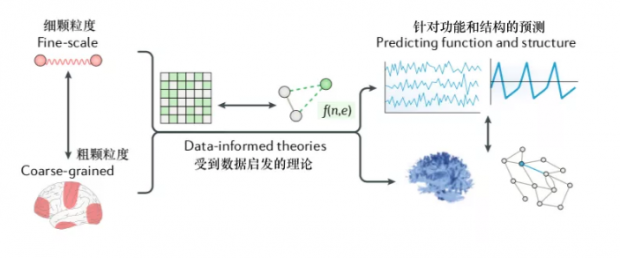
首先，结合针对同一个真实系统的细颗粒度信息与粗颗粒度信息，来创建基于数据表征的网络模型。这样的模型可以进一步启发基于理论的模型。理论模型，又可以用来预测基于功能现象或基于物理现实的模型中，所能观测到的功能或结构连接的模式。

作者：青子

审校：花花

编辑：李倩雨