导语

 

从15世纪下半叶至19世纪末的近代科学 ，到20世纪以来发展的现代科学，越来越多的科研工作者加入到了科学研究的队伍中，也产生了更加细化专业化的科学分支，如何发现有价值的科研兴趣？如何确定自己科研生涯的研究方向？如何能在提高科研产出数量的同时，增加自己文章被引率与影响力？当科学家站在科研工作的岔路口时，应当如何抉择？

 

近期，一个由北京师范大学、中国科学院、美国波士顿大学、以色列巴伊兰大学多位学者组成的研究团队，在Nature Communications上发表文章，以1893年至2010年间发表在美国物理学会（APS）期刊上的482566篇为例，通过书目耦合方法建立共引网络，描述了科学家文章之间的关系，并运用社团结构分析的方法将不同的研究兴趣具体化，进一步研究了科学家兴趣转移的趋势及动力学问题，提出了一个能解释科研兴趣转移机制主要特征的开发-探索模型。

 

---

 

随着论文数量的显著增长和科研投入的持续提高，对引文网络、科学政策、科研成效的研究越来越受到关注，逐渐形成了“科学学”（Science of Science）这一新兴领域。而科学家研究兴趣的转移问题，是这一领域的热点。

 

2019 年 7 月，由北京师范大学系统科学学院曾安、周建林、樊瑛、狄增如、王有贵，中科院国家科学图书馆沈哲思，与美国波士顿大学 Eugene Stanley 和以色列巴伊兰大学 Shlomo Havlin 等人组成的研究团队，在 Nature Communication 发表文章，系统分析了由美国物理学会 48 万篇历史文献的共引网络，提出了科学家兴趣转移的机制。

 

 

论文题目：

Increasing trend of scientists to switch between topics

论文地址：

https://www.nature.com/articles/s41467-019-11401-8

 

科学家共引网络的建立及其结构特性

 

共引网络的建立——书目耦合方法（Bibliographic Coupling）

 

文章基于美国物理学会（APS）期刊中消除姓名歧义后的236884位科学家的发表的482566篇论文数据，为3420位拥有50篇以上发表记录的科学家构建了联合引用网络（CCN），其中每个节点都是该科学家撰写的论文，如果两篇论文存在相同的参考文献，则将它们连接起来。在科学计量学中，这种基于节点（论文）的共同邻域构建节点（论文）之间链接的方法被称为书目耦合，并被广泛应用于分析其他各种实际系统，如国际贸易系统和在线社会系统。

 

社团结构分析——基于模块度优化的快速展开算法（fast unfolding algorithm）

 

文章利用快速展开算法识别科学家的每个共引网络的社团，该算法通过最大化模块度Q函数来检测社团。如果两篇论文共享至少一个参考文献，那么科学家的共同引文网络就是通过链接两篇论文而构建的。为了简单起见，文章不加权连边，仅考虑网络的拓扑结构。采用基于模块度优化的启发式快速展开算法检测网络的社团结构。文章考虑的模块化函数定义为：

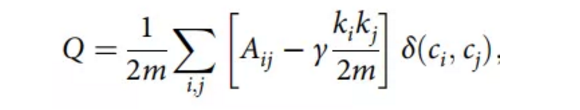
其中，Aij是共引网络的邻接矩阵的一个元素，ki是节点i的度，m是网络中的连边总数，ci是节点i被分配到的社团，如果ci=cj，则函数（ci，cj）为1，否则为0。函数Q最大化即可得到最优社团划分。注意：gamma是Q中的分辨率参数，标准模块函数中的gamma=1。较大的gamma参数可检测出较小但较多的社团，较小的gamma参数可检测出较大但较少的社团。需要说明的是，虽然社团数量的分布受到参数gamma的影响，但动力学特性的显示几乎与社团分辨率无关。因此，文章考虑了标准的模块化函数，即gamma=1。此外，为确保有意义的社团检测结果，需要共引网络规模需要足够大，也就是需要该作者有足够多的文章发表记录，因此，文章在研究中仅考虑在APS期刊上发表了至少50篇论文的3420位科学家。

 

共引网络拓扑性质分析

 

 

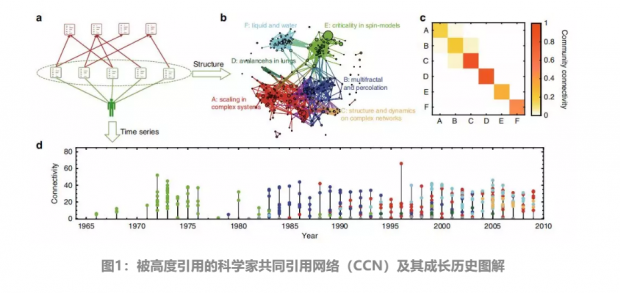
图1a展示了一位典型的被高度引用科学家的CCN的图解，用于展示构建共引网络的方法。其中，科学家写的论文用绿色标记，这些论文的参考文献用红色标记。

 

图1b展示的是由这位科学家发表的所有论文组成的共引网络。每篇论文由一个节点表示，如果两篇论文共享至少一个参考文献，则用一条连边将它们连接。采用快速展开算法对网络中的社团进行识别，可以看出该网络包含几个主要的大型社团、以及一些小型集群和孤立节点。

 

图1c展示的是社团连接矩阵，可以发现每个社团内的节点连接良好，但不同社团的节点连接较少。其中，社团连接性表示为文章之间的实际连边数与可能的最大连边数的比值。

 

图1d展示的是网络的发展历史，同时揭示了这位科学家在其职业生涯中是如何从一个研究课题转移到另一个研究课题的。在时间序列的子图中，每个点都是一篇文章，颜色对应于共引网络中的不同社团，点的高度是文章在网络中的连边数。

 

 

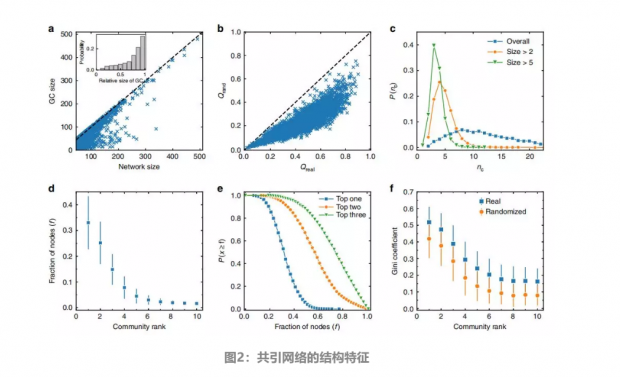
文章首先关注共引网络的结构性质。对于每个科学家的CCN，文章计算其最大连通子图（GC）的大小，并研究其与网络大小的相关性，如图2a中的散点图所示。可以看到，大多数点都位于对角线附近，这表明CCN通常是很好的连通性的并且具有相对较大的最大连通子图GC。同样的结论也可以在插图中得到，可以观察到GC相对大小的显著右偏分布。

 

在图1c中已经可以看出，CCN具有显著的社团结构。作为对这种现象的统计支持，文章在图2b中绘制了实际CCN中的最大模块度Qreal和其对应的随机化网络的最大模块度Qrand的分布值，可以看出Qrand显著小于Qreal。为了测量Qreal和Qrand之间差异的显著性，文章对每个科学家的CCN及其对应的随机化网络的模块度进行了单样本t检验。P值全部都显著小于0.01，表明CCN的模块度显著大于其对应的随机化网络，这表明真实网络中的社团结构是非常重要的。

 

鉴于论文倾向于在CCN中聚集成社团，一个有趣的问题是科学家拥有的社团的数量是多少？图2c显示了所有科学家的社团数量分布。文章在使用一个阈值来消除那些太小而不能被视为研究领域的社团后，科学家社团数量分布变得非常窄，如果只考虑文章数大于2和5的社团，则社团数量分别在4和3左右达到峰值。

 

为了更好地理解CCN中的社团大小，在图2d中显示了每个社团中按大小降序排序的节点分数。曲线的强烈衰减表明，大多数节点都属于几个主要社团。

 

对网络中几个最大社团中节点分数的反向累积概率进行深入研究，可以发现，对于一半的科学家来说，三个最大的社团包含了超过70%的论文，如图2e所示。

 

在图2f中，显示了不同社团中PACS码分布的基尼系数，其中社团按大小按降序排列，图中的误差线表示标准偏差。研究发现，真实数据中的平均基尼系数高于对应的随机化网络数据中的平均基尼系数，在相应基尼系数分布的Kolmogorov–Smirnov检验中，P值小于0.01。因此，研究表明，一个社团的论文倾向于共享相同的PACS代码，而被检测到的社团反映了科学家不同的研究领域。

 

社团转换概率的演化及其影响

 

 

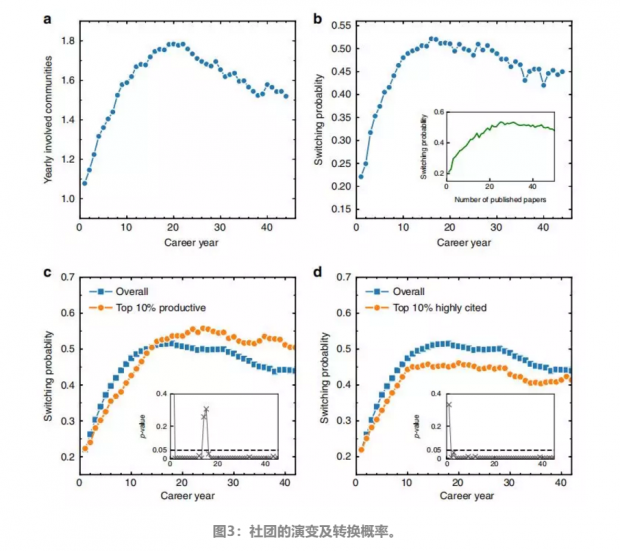
在在图1d展示的不同社团文章的时间序列的基础上，文章进一步研究了科学家对不同研究主题的兴趣转移动力学。图3a展示的是在整个职业生涯中，科学家每年参与主要社团的平均数量。图3b显示了职业生涯中平均转换概率的演变。转换概率的峰值在职业生涯的第20年左右，这表明科学家在职业生涯的早期转换较少，而在职业生涯的后期转换较多。为了进一步消除职业生涯中不同的文章产出数的影响，文章在图3b的插图中显示了转换概率与职业生涯中发表论文数量的关系。研究发现，职业生涯后期转换概率的衰减更加不明显，形成了转换概率的上升模式和下降模式。

 

文章进一步研究了交换概率与研究绩效之间的相关性。在这里，文章使用两个几乎不相关的指标来衡量科学家的研究绩效，即发表论文的数量和每篇论文的平均引用率。文章只考虑论文发表10年后的被引用次数，即C10。文章首先在图3c中比较了不同职业年中10%最具生产力科学家的转换概率和全部科学家的转换概率。文章意外地发现了两种相反的行为。在科学家的职业生涯早期（<12year），高的整体文章产出效率与低的转换概率相关，而在职业生涯后期，高的文章产出效率与高的转换概率相关。如果文章从引用率较高的科学家中剔除那些引用率低的科学家，这种模式仍然存在。导致这种模式的原因可能有多种，在早期职业生涯中，可能由于科学家对于自己的研究领域不再感兴趣，或研究方向的任务很难进一步研究，因而转换研究方向。这种现象导致文章产出效率和转换概率之间的负相关关系。

 

此外，文章在图3d中比较了论文平均引用率最高的10%的科学家的转换概率和全部科学家的转换概率。如图所示，在所有科学家职业生涯中，论文的高平均引用率与低转换概率相关。这一有趣的发现可能是因为较高的转换概率降低了在某一特定领域专家的印象，从而导致了较少的引用率。进一步，文章对转换概率进行了Kolmogorov–Smirnov检验。图3c与图3d的插图中所示的小P值大多数小于0.05。

 

 

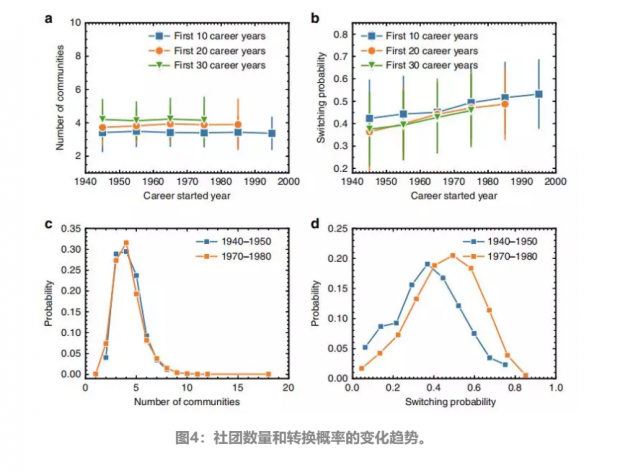
进一步，文章研究了近100年来，CCN的结构及其动力学性质是如何演化的。为了保证不同科学家的CCN之间比较的公平性，文章只考虑科学家前y年的职业生涯，去除所有尚未达到y年职业生涯的科学家，和在前y年的职业生涯中发表论文少于30篇的科学家。

 

文章首先选择了在某一年开始他们的职业生涯的科学家，并平均了这些科学家参与他们职业生涯的主要社团的数量。图4a中显示了在不同年份开始其职业生涯的科学家的平均社团数量。结果表明，随着科学的发展，科学家的主要社团平均数量几乎保持不变。

 

文章进一步计算了每个科学家在其职业生涯中的平均转换概率，并相应地通过平均每年开始其职业生涯的所有科学家的转换概率来计算每年的平均转换概率。图4b中的结果表明，尽管多年来社团的数量是稳定的，但从上个世纪开始，科学家在社团（主题）之间的转换越来越频繁。更具体地说，早期的科学家倾向于在转换到另一个话题之前在一个话题上工作更长的时间。相反，现在的科学家倾向于在多个社团中同时出现，导致社团之间的转换更加频繁。图4b中的误差线表示标准偏差。图4a、b中的大误差条是由于科学家在转换概率上的不均匀性造成的。

 

此外，文章通过直接研究两组科学家的社团数量和转换概率的分布来检验图4a与图4b中的结论。图4c及图4d表明，上世纪40年代出生的科学家与70年代出生的科学家相比，社团数量分布基本一致，但转换概率分布表现出显著的差异。

 

开发—探索模型——基于科研兴趣转移的动力学模型

 

文章提出了一个模型，用于定量化表示科学家兴趣转移动力学主要机制。科学家的研究活动可以模拟为知识空间中的发现过程（即表征不同知识之间联系的网络）。科学家发表论文时，会激活知识空间中的一个节点（即新知识）。这位科学家在其职业生涯中激活的子网络形成了一个个人网络，记录了他所有的论文以及其之间的联系。

 

节点激活过程的最简单模型是标准随机游走模型（RWM），假设科学家随机激活前一个激活节点的相邻节点。在这里，文章通过在随机游走模型中引入一个开发过程（由概率P控制）和一个探索过程（由概率Q控制），提出了一个开发-探索模型（EEM）。这两个过程都被指出是各种自适应系统创新的基础。在模型中，这两个过程是按顺序执行的。在每一步中，科学家不必总是从最后一个激活的节点开始，而是有可能从先前激活的节点中随机重新开发。一旦确定了重新开发的节点，科学家就有概率Q来探索最近邻居以外的节点（为了简单起见，是下一个最近邻居）。注意，当P=0和Q=0时，EEM模型就退化为RWM模型。

 

在模拟中，知识空间表示为一个由所有APS论文组成的网络，如果它们共享至少一个参考文献，则任何两个节点（论文）都将连接起来。每个科学家的第一个激活节点被设置为他的第一篇论文。每个科学家的其余论文是通过跟踪APS网络上的EEM模型生成的，直到激活节点的数量等于每个科学家论文的实际数量。

 

 

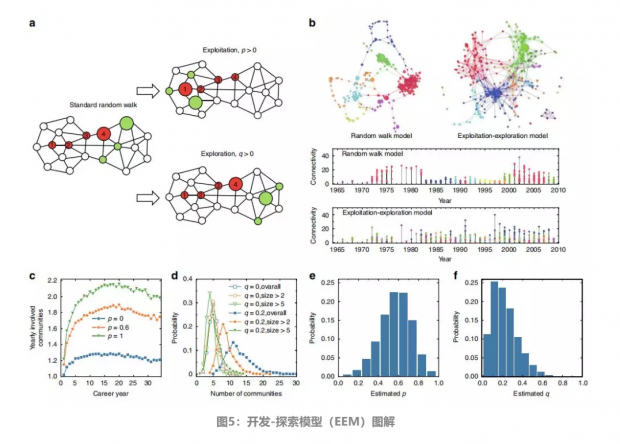
关于RWM模型和EEM模型的说明性演示，如图5a所示。图中的底层的网络是表示全部的知识空间，红色节点是科学家已经激活的节点，数字记录了节点被激活的步骤。节点激活过程的最简单模型是标准随机游动，假设科学家随机激活最后激活节点的相邻节点。因此，在图5a的左图中，红色节点4的一个相邻节点（用较大的绿色标记）将被随机地拾取和激活。但在EEM中，文章引入了一个开发过程和一个探索过程。利用概率P，科学家随机地重新开发一个先前激活的节点的邻域。在图中，科学家通过跳回到红色节点1并随机激活它的一个邻域进行开发。在概率Q下，科学家随机探索节点4的最近邻居以外的节点。为了简单起见，文章假设科学家在探索步骤中随机激活下一个最近的邻居。

 

文章首先通过模拟图1所示的具有代表性的高引用科学家的研究动态来测试EEM模型。具体而言，文章在图5b中比较了共引网络（CCN）以及由RWM和EEM生成的已发表论文的时间序列，包括初始论文和每年论文数量的参数设置与图1相同。可以发现，应用RWM生成的网络与图1b中的典型真实网络显著不同，因为它包含许多长链，并且缺少不同的社团。此外，从RWM获得的时间序列与图1d中所示的典型真实研究者的时间序列也有很大不同，因为每年都无法观察到社团之间的转换。相反地，由EEM生成的时间序列定性地再现了如图1所示的网络的类似特性。通过检验由该模型产生的一些统计量，可以定量化地证明EEM模型的优越性。

 

如图5c所示，第一个关系到不同P下每年参与的社团数量，当P=0时，每个科学家每年大概只在一个社团工作。随着P值的增加，每年参与的社团数量增加，当P=0.6时，每年参与的社团数量在1.8左右达到峰值，这是真实数据中观察到的值。这里，Q设置为0，因为它对每年参与的社团几乎没有影响。

 

另一个统计数字是每个科学家在其职业生涯中参与的社团数量。如图5d所示，当Q=0时，生成的子网没有明显的社团，因此社团的数量分布非常窄（即使对于所有检测到的社团都被视为社团的大小大于0的情况）。当Q=0.2时，社团大小>0、社团大小>2和社团大小>5的分布函数分别在11、8和5左右达到峰值，与图2c中的实际数据相似。这里，另一个参数P被设置为0，因为它对社团数量的分布几乎没有影响。

 

文章还根据实际数据估算了每位科学家的概率P和Q。文章把一位科学家发表的论文数记为ni。按照论文的顺序，如果一篇论文与科学家之前发表的任何一篇论文都没有参考价值，那就被认为是一种探索。文章将ui表示为科学家i的这类论文的总数，那么Qi可以很容易地估计为Qi=ui/ni。在科学家的论文序列中，如果一篇论文与其之前的论文至少有一个参考文献，则被认为是非开发性的。文章将vi表示为i的这类论文的总数，这样，可以将Pi估计为Pi=（ni-ui-vi）/（ni-ui）。 实际数据中估计的P和Q的概率密度函数分别如图5e、图5f所示。可以看到，P和Q的分布分别在0.6和0.2附近出现峰值，显示出与实际数据一致的统计特性。

 

 

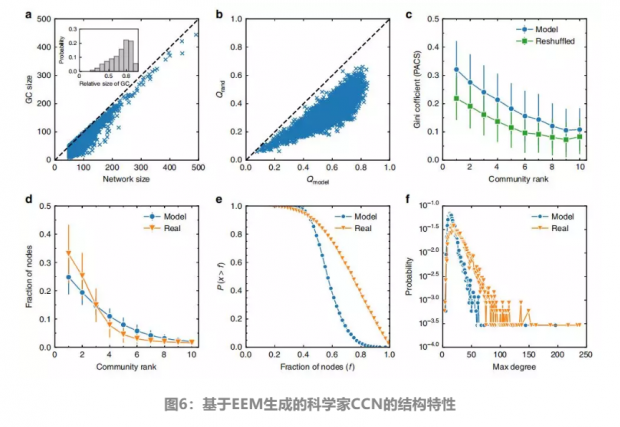
图6a显示了EEM模型生成的共引网络（CCN）的大小与其最大连通子图（GC）的大小之比。每一点都代表一个模拟科学家。图6b绘制了EEM模型生成的共引网络（CCN）中的最大模块度Qmodel和其对应的随机化网络的最大模块度Qrand的分布值。图6c展示了不同社团PACS码分布的基尼系数，其中社团按大小按降序排列，并将EEM模型数据与对应的随机化网络的PACS码进行比较，其中PACS码被重新匹配。图6d展示了真实数据和EEM模型数据在不同社团中的论文分数。图6e对于真实数据和EEM模型数据，三个最大社团中节点分数的逆累积概率。图6f展示了科学家真实数据和EEM模型数据的最大度分布。在这个图中，EEM的参数被选择为P=0.6和Q=0.2，误差条代表标准偏差。

 

最后，文章在图6中研究了基于参数P=0.6和Q=0.2的EEM模型生成的联合引用网络（CCN）的结构统计性质。尽管存在一些数量上的差异，但图2中测量的这些结构统计量在实际数据和模型数据中是相似的。特别是EEM生成的CCN具有良好的连通性和社团结构，社团中的论文共享相同的PACS码。在社团中同样发现了很强的规模非均匀性，这表明科学家在不同的主题中参与的比例非常不均匀。这些结果实际上是可以通过EEM模型预测的。文章将科学家的研究活动建模为知识空间中的发现过程，知识空间表示为所有APS论文的共引网络。底层网络已经具有非均匀规模和有意义的主题表示的社团结构。EEM模型从这个完整的网络中抽取的子网络自然具有这些特性。EEM模型的主要贡献在于它捕获了实际数据中科研兴趣转换行为的主要机制（即开发机制和探索机制），包括以较高转换概率转换回旧主题和较小的概率跳跃到小的孤立社团。

 

小结

 

主要研究结论

 

1.本文的科学家论文共同引用网络展示了清晰的社区结构，其中每个主要社团代表一个主要的研究方向。

 

2.科学家的主要课题的数量较少、分布很窄。

 

3.早期的研究人员倾向于在转换到另一个主题之前花更长的时间研究一个主题，而现在他们倾向于同时研究多个主题。

 

4.高生产率与职业生涯早期的低切换概率相关，而与职业生涯后期的高切换概率相关。与此形成鲜明对比的是，在所有的职业生涯中，每篇论文的高引用率与低转换概率相关。

 

5.文章提出了一个开发和探索机制模型来捕捉科学家兴趣转移动力学机制的主要特征。

 

文章推荐阅读

 

1.《Increasing trend of scientists to switch between topics》主要在科学家个人职业生涯中短期（逐篇文章）的尺度下，研究科学家兴趣转移的微观动力学问题。

 

2.下面展示的是在2017年发表在Nature Human Behaviour上的一篇文章《Quantifying patterns of research interest evolution》从宏观动力学角度研究科学家整个职业生涯中研究兴趣的转移机制，提出海滨漫步模型。两篇文章的研究结论大体上是一致的。

 

 

论文题目：

Quantifying patterns of research interest evolution

论文地址：

https://www.nature.com/articles/s41562-017-0078

 

作者：赵子鸣

审校：刘培源

编辑：张爽