导语

艾伯特-拉斯洛·巴拉巴西（Albert-LászlóBarabási）：畅销书《巴拉巴西成功定律》《爆发》作者，全球复杂网络研究第一人，全球复杂网络研究权威，“无标度网络理论”的创立者。美国物理学会院士，匈牙利科学院院士，欧洲科学院院士。

 

近期的新冠肺炎疫情让网络科学在流行病传播等领域的作用受到重视，《巴拉巴西网络科学》一书中针对此话题有不少观点讨论和成果展示，值得参考。本文系《巴里巴西网络科学》第9.7章节摘录。文中涉及其它章节的内容已标注。

 

目录

 

一、背景介绍

二、实时预测

三、假设分析

四、有效距离

五、小结

 

背景介绍

 

在历史的大部分时期，人类面对大规模流行病时总是束手无策。由于缺乏药物和疫苗，传染病一次次席卷全世界，夺走了大量的生命。直到1796年，才有第一支疫苗投入测试；直到20世纪90年代，针对新病原体的系统性的疫苗开发和治疗才成为可能。尽管医学发展进步巨大，我们也只是对少数病原体开发出了有效的疫苗。因此，降低传染率和基于隔离的措施仍然是卫生系统对抗新病原体的主要工具。为了让疫苗、治疗和隔离措施的组合手段生效，我们需要预测何时何地将出现下一次病原体暴发，从而让当地卫生机构优化部署可用资源。

 

关于流行病暴发的实时预测是近期才出现的研究领域，其发展基础来自20世纪80年代的传染病模型框架和2003年非典型性肺炎大暴发，后者确定了全球疫情的报告准则。随后出现的与流行病相关的可用数据为建模提供了实时输入。这些技术进展首次派上用场是在2009年H1N1甲型流感暴发期间——第一次实时预测了该流行病的传播。 

 

新病原体的出现总是伴随着几个关键问题：

病原体从哪里起源？

新发病例会出现在哪里？

流行病什么时候会到达各个人口稠密地区？

预计有多少人会被感染？

该如何减缓其传播进程？

如何能消灭它？

 

如今，这些问题都可以通过强大的流行病仿真工具来回答。仿真工具使用人口学信息、移动信息（图1，章节9.4）和流行病学数据作为输入。从随机种群模型到基于代理人的计算机仿真（可建模百万个体的行为和交互），都是这些工具背后的算法。在这一节中，我们将概述这些工具的用途，指出网络科学在这些技术发展中的作用。

 

实时预测

 

流行病预测旨在预判病原体的实时传播，即预测每个主要城市的每周受感染人数。基于网络科学的流行病实时预测的首个成功案例，并且得益于全球疾病传播和移动(Global Epidemic and Mobility，简称GLEAM)计算模型（图2，章节9.5），这一随机框架将全世界范围的高精度人口数据和移动数据作为输入，采用了基于网络的计算模型：

 

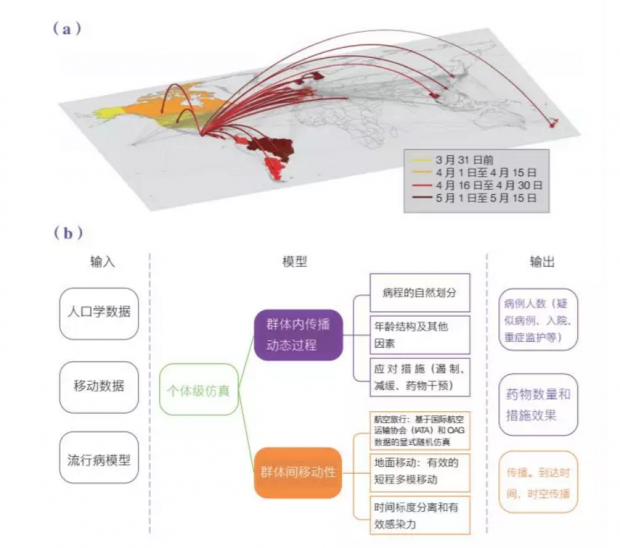
图1：2009年H1N1甲型流感传播建模

(a)H1N1甲型流感病毒在2009年暴发期早期的传播。箭头表示首个感染者到达之前未被感染的国家。颜色表示病毒到达的时间。

(b)GLEAM的计算模型流程图，用于预测H1N1甲型流感病毒和埃博拉病毒等病原体的实时传播。左栏（输入）表示输入的数据库，包括人口学信息、移动信息和流行病学信息；中栏（模型）描述了每一时间步建模的基于网络的动态过程；右栏（输出）是模型能预测的物理量的示例。

 

 

GLEAM将每个地理位置映射为网络中的节点。

根据全球交通数据（例如图1航线时刻表），用节点之间的传输表示链接（章节9.4）。

GLEAM使用基于网络的方法估算流行病参数，例如传播率和再生数。它基于历年全球范围流行病的传播数据，而非医学报告。

 

GLEAM实现了基于网络的流行病框架，给出未来数月内病原体在全球传播的多种可能的结果。对于H1N1甲型流感，我们将该模型的预测结果与48个国家在疫情全阶段从监测和病毒学来源与收集到的数据进行对比，有如下几点关键发现：

 

高峰期

 

高峰期是指某个国家病原体感染人数最多的一个星期。对高峰期的预测可以帮助卫生官员决定分配疫苗或治疗手段的时间和数量。高峰期与首个病例到达的时间，以及每个国家的人口学特征和移动行为特征等有关。在87%的国家中，观测到的高峰期均在预测区间内(图9-27)。剩下的国家中，观测的高峰期和预测的高峰期最多相差两星期。

 

早到的高峰期

 

GLEAM预测H1N1型流感的高峰期将出现在11月，而不是1月或2月——流感类病毒的常规高峰期。这个意外的预测结果后来被证实是正确的，进一步证明了模型的预测能力。高峰期提前是因为H1N1甲型流感原发地在墨西哥，而不像其它很多流感那样原发于南非，因此病毒到达北半球的时间提前了。

 

接种疫苗的影响

 

一些国家实施了疫苗接种运动来控制这次的疫情。仿真结果表明，这些大规模疫苗接种运动对这次流行病传染过程的影响几乎可以忽略不计。原因在于，疫苗接种运动的时间是根据1月高峰期预估推算的，因此都在2009年11月之后进行。而此时已经过了高峰期，很难有好的效果。

 

 

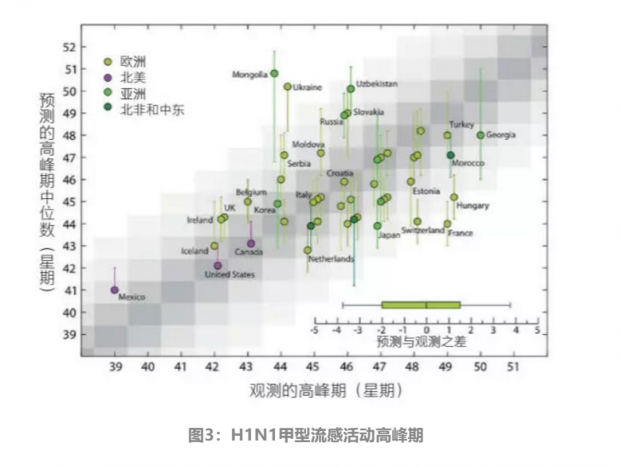
我们可以看到，图4示出的是多个国家中H1N1甲型流感病毒预测和观测的活动高峰期。高峰期是指病原体感染人数最多的一个星期，以距离流行病开始的星期数标识。模型通过分析2000次暴发的随机实现来预测，并生成了图中的误差线。

 

假设分析

 

通过考虑各种遏制、减缓措施的时间和性质，仿真可以估计各种应急方案的效果。接下来我们将讨论两种此类干预措施的影响。

 

旅行限制

 

由于航空旅行在病原体传播中扮演了重要角色，当我们面临埃博拉病毒这样的危险流行病时（图5），直觉上的首选方案就是限制旅行。然而在当今世界，航空运输有关键的作用，禁止航空旅行会导致经济崩溃。因此在实施航空禁令之前，我们必须确认限制旅行确实有助于控制疫情。其中一个很重要的认识是，“意识到病毒暴发”这件事本身就会减少旅行。例如，2009年5月，H1N1甲型流感暴发期间，进出墨西哥的人流量下降了40%——人们取消了在受感染地区进行的非必要商务和休闲活动。模型指出，这减少的40%使世界上各个国家的首个病例到达时间推迟了不超过3天。我们进一步认为，即使减少90%的旅行，高峰期的推迟也不会多于20天（图6）。

 

 

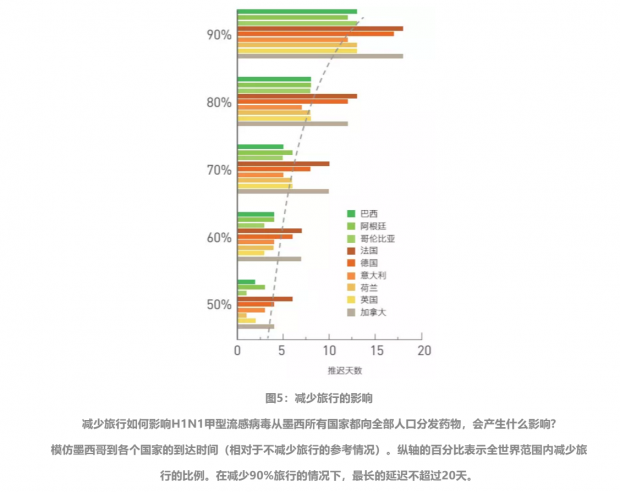
最重要的是，旅行限制并不会减少受感染人数，而只能延迟疫情暴发，让当地政府机构有更多的时间准备应对流行病。因此，只有当旅行限制所导致的延迟能够帮助提高当地疫苗接种水平或改善治疗手段时，旅行限制才是有效的。

 

抗病毒治疗

 

在2009年H1N1甲型流感传播时期，加拿大、德国、中国香港、日本、英国和美国都分发了抗病毒药物，来减轻这一传染病的影响。这不禁使人发问:如果有药物储备的真实验表明，高峰期会推迟3至4星期，从而使人们有更多的时间，让全部人口中更大比例的人在疫情达到高峰之前获得免疫。

 

有效距离

 

在汽车和飞机发明之前，病原体以步行速度，或最多以马车的速度进行传播。因此，像欧洲的黑死病这样的大规模疫情也以缓慢的速度从一个村子传播到另一个村子(图9-8)，其扩散过程可以用简单的反应-扩散模型(reaction-diffusionmodels)来描述。由于新增感染者总是跟之前的感染者存在地理邻近性，因此暴发时间曾与暴发地之间的物理距离存在很强的相关性。

 

而如今，有了航空旅行之后，物理距离失去了与疫情传播的相关性。曼哈顿出现的病原体可以很容易地到达伦敦，就像到达纽约州的加里森(Garrison)一样——后者距离曼哈顿只有一小时车程。这促使我们提出了一个问题:除了物理空间之外，有没有更好的观察流行病传播的空间呢?这样的空间是有的，只要我们把传统的地理距离替换为从移动网络中推算出的有效距离即可。移动网络的节点是城市，链接表示城市之间的出行量。链接是有向加权的，权值为流量比例(flux-fraction)0≤pij≤1，表示出行人群中离开节点 i 到达节点 j 的比例。pij的值可以从航线时刻表中抽取:仅当 i 到 j 有直接航线时，才有pij>0。

 

因为两个城市之间的路径可以有很多条，病原体也可以沿着移动网络上的多条路径传播。然而，决定实际传播的是由移动矩阵pij计算出的最大概率路径。这就可以使我们对两个相邻位置i和j之间的有效距离dij做出如下定义：dij=1-1pij≥0（图7）

 

 

如果pij较小，则只有很少比例的人离开 i 前往 j ，那么 i 和 j 之间的有效距离较大。注意dij=dij：小村庄 i 紧邻大城市 j ，我们认为dij很小，因为 i 中有很多人前往 j 。然而，dij很大，因为只有很少一部分人离开大城市前往小村庄。公式dij=1-1pij≥0中取对数使得有效距离可累加，对应于多步路径上的概率可连乘。

 

如图7所示，如果我们用公式dij=1-1pij≥0表示每个城市到流行病原发地的距离，则病原体以圆形波阵面(circular wave fronts)传播。相反，如果我们在物理距离空间观察流行病传播时，会看到非常复杂的传播模式。此外，H1N1甲型流感的到达时间关于物理距离的函数看起来非常随机，而其与有效距离之间却存在很强的相关性（图8）。因此，我们可以利用有效距离来确定病原体的传播速度（章节9.6）。

 

GLEAM预测的从3个初始暴发地区开始的疫情传播。虽然地理上的传播模式难以解释，但在用有效距离重新表示后，我们可以看到疫情传播遵循放射状模式（图7）。观察到的这一传播模式给我们提出了一个问题:一个典型的病原体在全球传播的速度是怎样的呢？速度取决于3个关键参数：

 

(1)基本再生数R0。流感类病毒大约为2。

(2)康复概率。流感大约3天。

(3)移动率，即每天出行的人占总人口的比例。通常介于0.001～0.01之间。

 

输入这些参数运行GLEAM（图2），我们可以计算到达时间和与传染病原发地之间的地理距离的相关性，得到病毒大约每天传播250～300公里。因此，流感病毒在大洲内部的传播速度相当于跑车或者小型飞机。

 

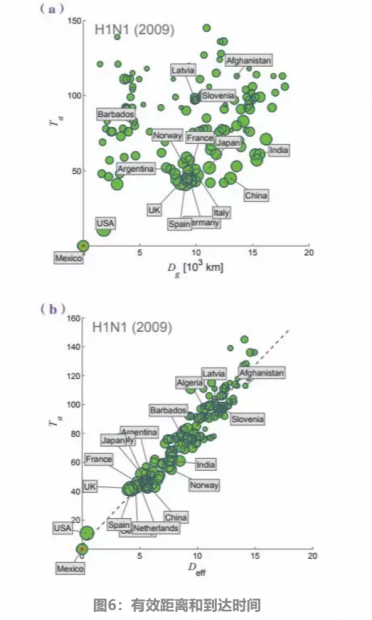
(a)地理距离：2009年H1N1甲型流感期间的到达时间与原发地（也就是墨西哥）的地理距离。每个圆圈表示140个受感染国家之一，其大小代表这个国家的总交通流量。到达时间是指2009年3月17日疫情暴发后，每个国家的第一个确诊病例的日期。图中到达时间和地理距离在很大程度上是相互独立的(R0=0.0394)。

(b)有效距离：H1N1甲型流感到达时间Ta与有效距离Ta。图中表现出有效距离公式dij=1-1pij≥0到达时间的强相关关系。

 

传染病预测问题有一个令人惊讶但喜闻乐见的方面:即使使用不同的移动数据（航线时刻表或美元移动）、假设不同的流行病参数（康复概率、传播率等），各种模型的估计结果也都非常接近。而有效距离可以帮助我们理解为什么不同的模型会给出相近的预测。事实上，我们可以把病原体到达位置a的时间写作：

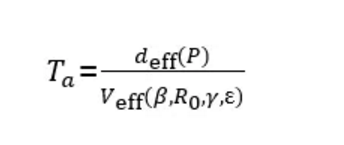
因此，到达时间等于有效距离deff和有效速度Veff之比。有效速度只取决于病原体的流行病学参数，而有效距离deff只取决于移动网络的拓扑结构——链接权重pij。在出现新的流行病暴发时，一开始我们并不知道其病原体的流行病学参数。然而，上述公式说明相对到达时间是与流行病学参数无关的。例如，对于节点i开始的流行病暴发，其到达节点 j 和节点l的时间之比为：

即该比例仅取决于有效距离。因此，传染病的相对到达时间只取决于移动网络的拓扑结构。由于全世界范围内的移动模式是唯一的且与模型无关，因此不同模型的预测结果也几乎一致——与其各自选取的流行病学参数无关。

 

总而言之，数据的收集和网络上的传染病研究的进步共同促使实时预测病原体传播成为可能。所开发的模型可以帮助设计应对和缓解方案，训练医疗和急诊人员，还可以用于探索从隔离到旅行限制等不同干预措施的影响，优化治疗和疫苗的分配。

 

有趣的是，流行病预测在近期取得成功并不是因为人们对传染性病原体的生物属性有了进一步的认识。应该说这是一种很幸运的情况，当涉及病原体传播时，其流行病学参数并不是最重要的。最重要的因素是移动网络的拓扑结构。而这一结构可以从旅行日程表中准确构建出来，从而使我们可以从人类的移动模式中得到关于流行病传播的准确预测。

 

小结

 

大多数网络都是沿着其链接进行传播的，包括传播信任、知识、习惯或信息（社交网络）、电力（电网）、货币（金融网络）、商品（贸易网络）等。要理解这些现象，必须理解网络拓扑是如何影响其动态传播过程的。在这一章，我们关注病原体沿着网络的链接进行传播的现象。在这一领域，我们关于动态现象和网络拓扑之间相互作用的理解是最前沿的。我们发现，网络拓扑结构对动态传播的过程有极大的影响——随机网络和无标度网络上的传播会产生截然不同的结果。这一发现也为解决更广泛的一类问题奠定了基础，即系统地理解网络对不同动态过程的影响。而这也成了网络科学领域越来越活跃的一个课题。

 

建模病原体的传播也是网络科学的一个重要实践应用。这一领域所取得的进展是令人瞩目的：我们实现了对流行病的精确预测，而这在十年前还只是一个梦。这一进展得益于两方面的进步：一是出现了鲁棒的理论框架来描述基于网络的流行病；二是可以获取实时的人类旅行和人口学数据，使我们得以重构引发病原体在全球范围内传播的移动网络。如我们所看到的，生物属性和网络结构对模型预测能力的准确性都有各自的贡献，但并非紧密结合的。因此，如果需要一个准确的预测，首先就要对移动网络有一个准确的了解。

 

网络上的流行病分析框架给出了很多让人意想不到的结果，其中最重要的一个结果是:在异质网络上，特征传播时间和传播阈值趋近于零。由于流行病传播所涉及的接触网络大多具有较宽的度分布，这些结果同时具有短期和长期的理论与应用价值。

 

同样重要的还有网络上的流行病学对于免疫策略所提供的支持。如我们所展示的，虽然随机免疫能够成功地消灭在随机网络上传播的病毒，但这一策略并不适用于无标度网络。而由于大多数接触网络都是异质网络，这是一个相当令人沮丧的结论。不过，我们发现选择性免疫策略可以让传播阈值回到零以上，进而阻止病原体的蔓延。这一策略的成功是因为它系统地改变了病原体传播的网络拓扑结构。

 

作者：艾伯特－拉斯洛 · 巴拉巴西

编辑：张希妍