导语

 

诺贝尔物理学奖得主、著名凝聚态物理学家菲利普·安德森（Philip W. Anderson）于美国时间 3 月 29 日逝世，享年 96 岁（1923.12.13-2020.03.29）。

 

菲利普·安德森是凝聚态物理学的主要奠基人，致力于推动复杂性科学与跨学科研究，是圣塔菲研究所的发起人之一。他于1972年在Science发表了题为“More is Different”的论文，通过介绍在各个尺度的物理系统都普遍存在的“对称性”和对称性破缺，对“还原论”思想提出了深刻的质疑。我们曾对这篇经典论文做了全文翻译，旧文重发，供读者参考。

 

 

论文题目：

 

More is different：Broken Symmetry and the Nature of the Hierarchical Structure of Science

 

论文地址：

 

https://science.sciencemag.org/content/177/4047/393

 

还原论（reductionist）假说在哲学家中或许仍具争议，但我认为，该假说无疑已被绝大多数活跃的科学家所接受了。我们的思维和身体的运作，以及我们所知的任何有生命的或无生命的物质的运作，被认为是被相同的一套基本定律所控制的。除了在某些极端情况下基本定律可能失效，我们已经非常了解这些基本定律。

 

以下结论似乎是还原论的显然推论：如果万事万物遵循相同的基本定律，那么只有研究真正基础的事物的科学家才是研究基本定律的人，也就是指某些天体物理学家、粒子物理学家、逻辑学家、数学家以及极少数的其他学科的科学家。这种观点，也就是本文旨在反驳的观点，在 Weisskopf 一篇非常著名的文章中也有所表示：

 

纵观 20 世纪的科学发展，我们可以发现两种趋势。因缺乏更好的术语表达，我姑且称其为“内涵性（intensive）研究”和“外延性（extensive）研究”。简而言之，内涵性研究旨在研究基本定律，外延性研究旨在根据已知的基本定律解释现象。这种区分并不是绝对的，但是大多数情况下是清晰的。固体物理学、等离子体物理学和生物学属于外延性研究。高能物理学和原子核物理学的绝大部分内容属于内涵性研究。正在进行的内涵性研究总是比外延性研究少得多。一旦发现新的基本定律，大量的研究开始考虑将这些发现应用于迄今未解的现象。因此，基础研究有两个维度。科学的边界延伸地非常远，从最新潮的内涵性研究，到由最新的内涵性研究引发的外延性研究，再到基于过去数十年的内涵性研究的广泛而成熟的外延性研究网络。

 

这种观点曾被材料科学领域的一位领军人物引用，由此可见该观点的影响力。该领军人物敦促一个致力于“凝聚态物理学的基础问题”的会议的与会者接受这样一个观点，即在该领域中，这样的基础问题极少甚至几乎没有，并且该领域现在仅剩外延性研究，而他将这种外延性研究戏称为设备工程（device engineering）。

 

这种想法的主要谬误在于还原论假说从来都不意味着“建构论（constructionist）”假说：将所有事物还原为简单的基本定律的能力并不意味着从那些基本定律出发并重建整个宇宙的能力。事实上，粒子物理学家告诉我们越多关于基本定律的本质，这些基本定律和其他学科的问题的关联越少，和社会问题的关联也越少。

 

在面对尺度（Scale）和复杂性（Complexity）的孪生难题时，建构论假说轰然瓦解。事实证明，我们无法根据少数粒子的性质的简单外推，来理解大量且复杂的基本粒子集合体的行为。相反的，在任何不同的复杂性层级下，物质会出现全新的性质。并且，对新性质的理解需要本质上一样的基础研究。因此，我认为可以基于下述设想粗略地将学科线性排列在一个层级结构中：学科 X 的基本实体遵循学科 Y 的定律。

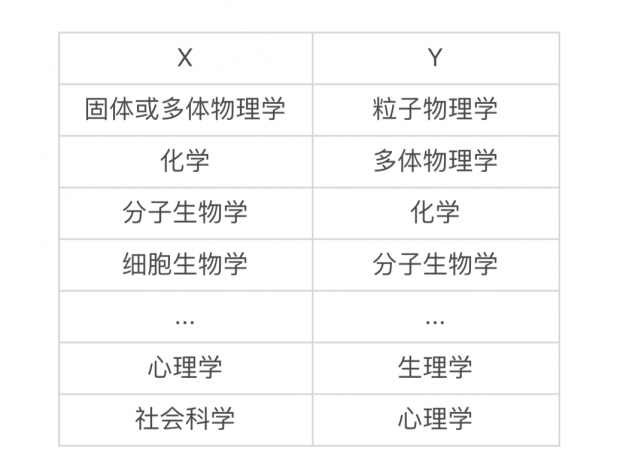
然而，这个层级结构并不意味着学科 X “仅仅是Y的应用”。每个新的层级都需要全新的定律、概念和归纳，并且和其前一个层级一样，研究过程需要大量的灵感和创意。心理学不是应用生物学，生物学也不是应用化学。

 

 

对称性破缺

 

我自己所在的领域，多体物理学，或许比其他任何学科更接近基础的内涵性研究。该领域中存在非平凡的*复杂性（non-trivial complexities），于是，我们开始构想一个一般化的理论，来说明从定量到定性的转变是如何发生的。这一理论构想，被称为“对称性破缺（broken-symmetry）*”理论，或许有助于让还原主义的对立面——构建主义——的瓦解更加清晰。我将给出这些观点的基础且尚不完善的解释，然后将给出关于其他层级的类似现象的更一般化的推断性解释。

 

*non-trivial 在数学，物理与计算科学中被广泛用于描述对研究员来讲不直观或者不容易证明的问题，non-trivial与trivial之间并没有明显界限。

 

*对称性破缺可以粗略理解为原来具有较高对称性的系统，出现不对称因素，其对称程度自发降低的现象。

 

首先需要澄清两点：

 

一，当我说尺度变化导致根本性变化时，我并不是在说那个广为人知的观点，即新尺度下的现象遵循完全不同的基本定律——比如，宇宙尺度遵循广义相对论，原子尺度遵循量子力学。我想大家应该都承认，所有普通物质都遵循简单的电动力学和量子论，这也是我所讨论的范畴。（正如我所说的，我们必须从我们深信不疑的还原论出发。）

 

误解之二源于粒子物理学家借用了对称性破缺这一概念的事实，不过他们对该术语的使用只是一个类比，其表达的是深层含义还是浅层含义仍有待商榷。

 

我将用一个尽可能简单的层级中的实例开始我的讨论，我在读研的时候接触过它：氨分子。那个时候，每个人都对氨有所了解，并用其来校准自己的理论和仪器，我也不例外。化学家会说氨“是”一个三棱锥，氮原子带负电，氢原子带正电，因此氨有一个电偶极矩（μ），且负向指向棱锥的顶端。我很难理解化学家的观点，因为以前的老师告诉我不存在有电偶极矩的物质。那位教授真的证明了原子核不可能有偶极矩，因为他是教授核物理学，不过，因为他的讨论是基于时空对称性的，所以他应提供了具有普遍性的结论。

 

 

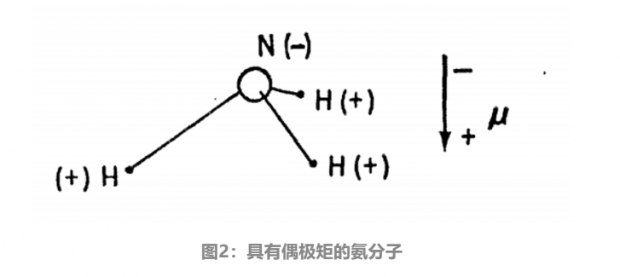
我很快发现，物理学家的这些观点是正确的（或者更准确的说法是这些观点不是错误的），因为教授的表述非常谨慎：没有任何系统的定态（stationary state，即不随时间变化的状态）存在电偶极矩。如果氨分子开始时是上述的非对称态（即具有偶极矩的状态），它无法保持该态很长的时间。由于存在量子隧道效应，氮原子可以通过氢原子组成的三角形泄露到另一侧，将棱锥颠倒，这个过程实际上发生地非常快。这也就是所谓的“反转（inversion）”，发生频率为每秒 3 X 10^10 。真正的定态只能是不对称棱锥和其反转的等权叠加。那种混合状态不存在偶极矩。（读者值得注意的是，这里是高度简化的说法，详细内容请查阅教科书。）

 

我不打算描述整个证明过程，但结论就是，如果一个系统状态是定态，那么它一定拥有与控制它运动的动力学一样的对称性。原因很简单：在量子力学中，除非存在对称性的限制，系统总是存在从一个态变化到另一个态的方法。因此，如果我们从任何非对称态出发，系统将转变为其他态，所以只有以对称的方式叠加所有可能的非对称态，我们才能得到定态。氨分子涉及的对称性是宇称（parity，即空间反演对称）——宇称的粒子左手性与右手性等价。（关于基本粒子实验人员发现的特定违背宇称现象的条件和本问题无关；那些条件能造成的影响太弱了以至于无法影响普通物质。）

 

我们已经知道了氨分子如何满足没有偶极矩背后的理论分析，现在我们开始考虑其他的情况，特别是当系统渐进宏观时，以判断态和对称性是否总是相关的。自然界中存在着和氨类似的金字塔状的分子，由原子量更大的元素组成。磷化氢，PH3，是氨的两倍重，也会反转，不过频率是氨的十分之一。三氟化磷中，PF3，更重的氟原子取代了氢原子，尽管理论上我们可以确定反转的发生，但是我们无法在可测水平中观测到三氟化磷的反转。

 

接下来我们考虑更复杂的分子，比如含有 40 个原子的糖分子。在这种尺度下，期待分子反转是没有意义的。生命有机体产生的糖分子都具有稳定的同一螺旋方向（左旋），此时糖分子左手性与右手性不等价，也就不具备宇称对称性。并且，无论是量子力学隧道效应还是常温下的热扰动都无法使其反转。此时研究糖分子的性质必须抛开反转的可能性并忽略宇称对称性（parity symmetry）：对称性定律没有被违背，而是破缺了。

 

 

另一方面，如果我们通过热平衡中的化学反应合成糖分子，我们会发现，一般情况下，左手性分子和右手性分子的数量是一样的。如果没有比自由分子集合体更复杂的物质，一般而言，对称性定律不会被打破。我们需要生命体来产生不同对称性分子分布的不均匀性。

 

大规模的但是无生命的原子聚合物中，会出现一种完全不同的对称性破缺，从而导致净偶极矩（net dipole moment）或者净旋光度（net optical rotating power）的产生*，或同时导致两者。很多晶体在每个晶胞（晶体的最小重复单位）都存在一个净偶极矩（热电性 pyroelectricity），并且某些基本单元的矩可被电场反转（铁电性 ferroelectricity，指的是外加电场可以改变偶极矩方向，这种性质被称为铁电性）。这种非对称性是晶体寻求到达其最低能量态时的自发效应。当然，具有相反矩的态也存在，并且对称地具有相同的能量，但是因为系统如此之大，以至于没有热力或量子力能够在有限的时间中（相较于宇宙的年龄），将一种态转换为另一种。

 

*净偶极距指的是分子的化学键具备偶极矩，但由于组成分子的偶极矩在空间各个方向上抵消，最后分子总偶极矩体现为分量的矢量合。

 

基于此至少可以得到三个推论：

 

一，对称性在物理学中意义重大。对称性意味着即便观察者视角不同，系统仍然具备原来的特质。可以说，物理学是研究对称性的学科。牛顿第一次展示了该观点的威力，他或许会问自己：如果我手里的物体和天空中的物体遵循相同的定律会怎样——如果空间和物质是相同的且各方向同性的会怎样？

 

二，即使一个物体的总态（total state）是对称的，其内部结构并不一定是对称的。我们可以从量子力学的基本定律出发并预测氨分子的反转和其易被观察到的性质，而无需穷尽非对称的金字塔状结构的态，尽管没有“态”有那种结构（意为从严谨的物理学角度，氨分子并不是金字塔结构的）。直到几十年前，核物理学家才停止将原子核视为没有特征的、对称的小球。并且，他们开始意识到，尽管原子核没有偶极矩，但并不妨碍原子的电子云变成橄榄球状或盘子状。这个结果能够在核物理学所研究的反应光谱和激发光谱中观察到，尽管其比氨反转更难以被直接证明。在我看来，无论是否将其称为内涵性研究，它都和人们所认为的本质规律一样基础。然而，这个现象并不不需要新的基本定律去解释，并且从那些已有定律中将其推导出来十分困难；它仅仅是一个基于日常直觉的灵感，突然就和其他所有事物契合地非常好。

 

这个结果很难推导的原因是我们接下来需要讨论的重要问题之一。如果原子核足够小，我们没有能够严格定义其形状的方法：我们无法将数个缠绕的粒子定义为旋转的“盘子”或“橄榄球”。只有将原子核视为一个多体系统——也就是 N→∞ 极限 —— 才能说定义形状是严谨的。那样形状的宏观物体将具有一个所谓的旋转或震动激发光谱，并且本质上和无特征系统（featureless system）完全不同。当我们看到这样的光谱时，尽管并不是那么清晰和完美，我们仍然会承认原子核不是宏观的，它仅仅是趋近于宏观。从基础定律和计算机出发，我们不得不实现两件不可能的事情——解决无限多体的问题，并将其运用于有限的系统——在我们实验制备之前。

 

三，一个足够大的系统的态不一定遵循对称性定律；事实上，其通常具有较低的对称性。例如，晶体由原子和空间依据完美的空间齐性（homogeneous space）构成，但晶体却突然毫无征兆地展现了全新且美妙的对称性。然而，更一般化的规则是大系统较其底层结构具有更低的对称性，晶体也不例外：尽管晶体具有对称性，但其对称性远低于完美空间齐性情况。

 

晶体的例子中我的论证也许过于模糊粗浅。但是19世纪中期，晶体的规律性就已被半经验地推导了出来，并且丝毫不需要复杂的论证。但是某些时候，如超导性，新的对称性——现在我们称其为破缺的对称性，因为原始的对称性不再明显了——是让人完全难以预测和直观理解的。从知晓超导性的基本定律，到真正做出超导现象的解释，物理学家用了 30 年。

 

超导性是对称性破缺的最为突出的宏观实例，但其并不是唯一的实例。反铁磁体、铁电体、液晶等都遵循一个特定的、非常普遍的规则和理念，那就是一些多体物理学家所谓的对称性破缺。我不会继续讨论这段历史，但是在文章末尾给了一个参考目录。

 

问题的关键是，在大系统（就我们而言的宏观尺度）的N →∞ 极限中，物质会经历数学上尖锐的、奇异的“相变”，最终到达违反微观对称性甚至微观运动方程的态。对称性只在一些特定的性质上有所体现，比如长波振动，一个我们非常熟悉的例子就是声波；或超导体不同寻常的宏观导电现象；还有晶体点阵和大多数固体的刚性。当然，系统不是真的在违背（violate）时空对称性，而是表现出一种对称性破缺（break），但是从能量角度考虑，系统各部分保持固定关系是更有利的，因此对称性只允许整体对外力做出回应。

 

这导致了“刚性”，也是超导性和超流性的恰当描述，尽管它们有显然的“流体”性质。（London 很早就注意到了超导性。） 事实上，对于假想的木星上的气态智慧公民，或者银河中心某处的氢云中的公民，普通晶体的性质很可能比超流氮更复杂和令人困惑。

 

我并不想让大家以为所有问题已经解决了。例如，我认为，玻璃以及非晶体仍然存在令人着迷的原理性问题，这些问题的解决或许会揭示更复杂的性质。然而，我们至少已理解了在惰性宏观的物体的性质中，这类对称性破缺在理论层面充当的角色。在这种情况下我们发现，整体不仅仅多于部分之和，并且不同于部分之和。

 

接下来我们会很自然地考虑，时空的基础对称性是否有更彻底的瓦解，是否会产生新的、本质上不同于“简单”相变（即凝结态到具有更低对称性的态）的现象。

 

我们已经排除了显然不对称的液体、气体和玻璃的情况。（实际上它们比我们想象地更为对称。）下一个阶段应该考虑规律的但是包含信息的系统，也就是说该系统在空间上是规律的，因而可以被“读出（read out）”，但是相邻单元有不同的元素。一个显然的例子是 DNA；日常生活中，一行字或一卷电影胶片也具有相同的结构。这种“载有信息的结晶性”似乎对生命至关重要。生命的发展是否需要进一步的对称性破缺尚不清楚。

 

科学层级结构的本质

 

继续探讨生命体中的对称性破缺，我发现至少还有一种现象是可识别的，并且是相当普遍的，即时间维度的次序（ordering），也可称之为时间维度的规律性（regularity）或周期性（periodicity）。大量关于生命过程的理论中，时间上的规则脉动都非常重要：关于发育、生长、生长极限理论和记忆理论。时间规律性在生命体中非常普遍，且至少起着两方面的作用。一，大多数从环境中获取能量以确保持续、准稳态过程的方法牵涉到时间周期装置（time-periodic machines），比如振荡器（oscillator）和发生器（generator），生命过程也不例外。二，时间规律性是一种处理信息的方法，和信息携带的空间规律性类似，人类的口语是一个实例。此外，值得注意的是，所有的计算机都使用时间脉冲。上述提到的理论也暗示了第三方面的作用：利用时序脉冲的相位关系来处理信息并控制细胞和有机体的生长和发育。

 

在某种意义上，结构——目的论（teleological）意义上的功能性结构，而不仅仅是晶体的形态结构——必须被认为是对称性破缺等级结构中的一个阶段，可能是处于结晶性（crystallinity）和携带信息的字符串（information strings） 之间的阶段。

 

基于层层推测，我觉得下一个阶段是功能的层级结构或专门化，或者同时包括两者。某种意义上，我们应该停止讨论降低的对称性，而将其称为增加的复杂性。因此，随着每个层级的复杂性不断增加，我们沿着学科的层级结构上升。在将复杂性较低的部分组合为更复杂的系统、并理解由此导致的新性质的过程中，我们在每个层级都会遇到迷人的且基础的问题。

 

多体理论和化学等简单情况中复杂性出现的方式，不能类比于真正复杂的文化和生物情况中复杂性出现的方式，除非，泛泛地认为系统与其组成部分的关系是单向的。综合是几乎是不可能的；另一方面，分析不仅仅是可能的，并且各个方面都是富有成效的：如果没有理解超导体中的对称性破缺，Josephson 可能不会发现约瑟夫森效应。（约瑟夫逊效应的另一个名字是“宏观量子干涉现象”：超导体电子或超流氮中的氮原子的宏观波函数之间的干涉效应。这些现象极大地提高了电磁观测的精度，并且有望在未来的计算机中发挥重大作用，因而最终导致划时代的技术进步。）再举一个例子，在将遗传学还原为生物化学和生物物理学的过程中，生物学发生了极大的改变，这将带来无法估量的重大发现。因此，最近一篇文章中的观点是不对的：我们每个人应该“耕耘我们自己的谷地，而不要尝试在学科之间建造跨越山脉的道路”。相反的，我们应该意识到这样的道路，不如说是通向我们自己学科其余部分内容的最快捷径，仅从单一学科的视角是看不到的。

 

粒子物理学家的自大和他的内涵性研究可能已经被我们抛在身后（正电子的发现者曾称“剩下的都是化学”），但是我们仍然没有从一些分子生物学家的自大中恢复过来，这些生物学家似乎坚定地尝试将人类有机体的所有事物还原为“仅仅是”化学，范围从普通的感冒和所有的精神疾病到宗教本能（religious instinct）。显然，人类行为学和 DNA 之间的组织层次比 DNA 和量子电动力学之间更多，并且每个层级都需要全新的概念结构。

 

最后，我想借用两个经济学的例子。马克思曾说量变导致质变，但是1920 年代巴黎的一段对话将该观点概括地更加清楚：

 

菲茨杰拉德：富人和我们不同。

 

海明威：是的，他们有更多的钱。

 

参考文献：

 

[1] V. F. Weisskopf, in Brookhaven Nat. Lab. Publ. 888T360 (1965). Also see Nuovo Cimento Suppl. Ser 1 4, 465 (1966); Phy. Today 20 (No. 5), 23 (1967).

 

[2] A. Bohr and B. R. Mottelson, Kgl. Dan. Vidensk. Selsk. Mat Fys. Medd. 27, 16 (1953).

 

[3] Broken symmetry and phase transitions: L. D. Landau, Phys. Z. Sowjetunion 11, 26, 542 (1937). Broken symmetry and collective motion, general: J. Goldstone, A. Salam, S. Weinberg, Phys. Rev. 127, 965 (1962); P. W. Anderson, Concepts in Solids (Benjamin, New York, 1963), pp. 175-182; B. D. Josephson, thesis, Trinity College, Cambridge University (1962). Special cases: antiferromagnetism, P. W. Anderson, Phys. Rev. 86, 694 (1952); super-conductivity, ——, ibid. 110, 827 (1958); ibid. 112, 1900 (1958); Y. Nambu, ibid. 117, 648 (1960).

 

[4] F. London, Superfluids (Wiley, New York,1950), vol. 1.

 

[5] M. H. Cohen, J. Theor. Biol. 31, 101 (1971).

 

[6] J. Clarke, Amer. J. Phys. 38, 1075 (1969); P. W. Anderson, Phys. Today 23 (No. 11), 23 (1970).

 

[7] A. B. Pippard, Reconciling Physics with Reality (Cambridge Univ. Press, London, 1972).

 

翻译：曾小欢

 

审校：陈曦、刘金国

 

编辑：张爽