Nature物理：怎样让信息传遍全网？突破社区的临界相变点-集智俱乐部的财新博客-财新网

导语

每当我们看到谣言都会感叹，为何相比辟谣帖，谣言的传播能又快又广。最近美国东北大学复杂网络学者 Alessandro Vespignani 等人组成的研究团队，在 Nature Physics 发表论文，尝试解答这个问题。研究者首先介绍如何对信息的传播建模，之后分析了对针对不同社会结构的两种建模方式，讨论社会网络中信息传播范围与传播效率中存在雪崩式演化的临界相变点。

论文题目：

Phase transitions in information spreading on structured populations

论文地址：

https://www.nature.com/articles/s41567-020-0810-3

信息传播的三种状态

针对人类相互作用网络的社会传播模型，近年来越来越流行。然而这些模型很难应对社会技术系统的复杂性和现实挑战。在这篇论文中，研究者通过分析 Maki-Thompson 这个经典的谣言传播模型，发现了其中蕴含着的临界相变。

类似于例如SIR这样的疾病传播模型，针对信息传播的 Maki–Thompson模型，也将人群分为了三种状态，分别是：

未知者，即没有听到这则消息；

传播者，了解并积极传播消息者；

沉默者，即了解信息但不会再传播信息。

对于不同的信息，如果传播者将该信息告诉未知者，那么有 λ 的概率，会让未知者成为传播者。

如果传播者将这个信息传给其他传播者或者沉默者，那么有 α 的概率，传播者会由于这个信息已不再新鲜，而变成沉默者。

假设人群是均匀分布的，即网络中每个人都是一样的，不存在某些人之间交流的比例更高、某些人之间交流的比例更小，那么，信息最终能传播到多少比例的人，只取决于上述两个参数的比值，即传播的比例与不再传播的比例。

如果传播成功的概率和沉默的概率相同，则最终这则消息会传遍全网络。

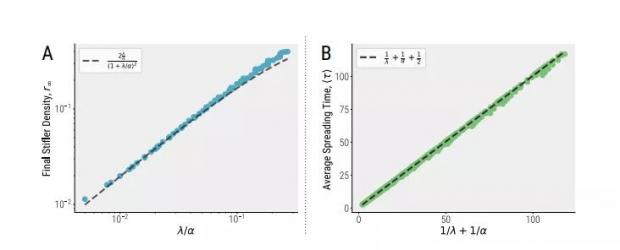
图1：传播/不传播概率比值与最终网络传播程度的关系

如图所示，在人群均一时，传播的结果（最终有多少人知道这则消息及传播速度）只由概率 α 和概率 λ 决定。

对于谣言传播来说，传谣者的人数只要达到和不传谣者一样多，就能让谣言传遍全网。

城市社区与虚拟社区

现实中的人各有不同，有些人之间的交往多一些，有形形色色的小圈子，形成了所谓的社会结构。在模型引入了社会结构之后，就会出现非线性的临界点。

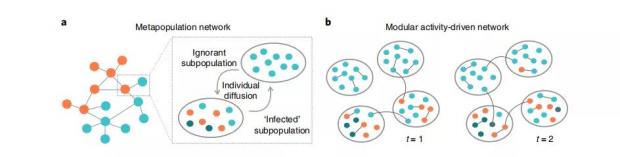
图2：人群结构建模的两种方式对比图

上图展示了大都市网络（固定社区）和虚拟社区网络两种建模方式。

左图 a 是大都市网络，在《巴拉巴西的网络科学》这本书有详细介绍，指人群分为多个区块，每个区块的平均人数为 N。区域内的人先在内部进行信息传播，之后以 p/k 的概率向区域外的人传播，其中 p 为传播概率，k 为与该区域相连的其他区域的数量。

相比基于地域的大都市网络，右图 b 代表的虚拟社区的传播模型，适合对网络论坛，兴趣小组建模。模型将人群分成了 V 个社区，社区的大小符合特定概率分布。每个用户在每个时刻，有可能变得活跃，之后以 μ 的概率和本社区的人交流，以 1-μ 的概率建立一条跨社区的连接，如此一步步形成信息传播的网络。

需要足够多的跨社群连接，才能让信息传播开

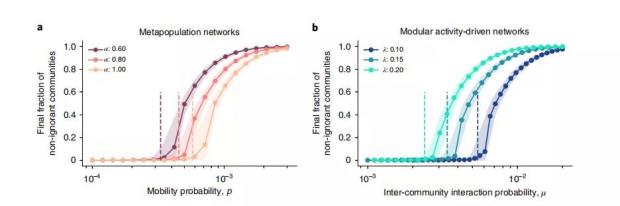
图3：大都市网络和虚拟社区下信息传播结果对比

如图所示，研究者跟上述假设构建模型，通过多次蒙特卡罗模拟，在只有一个初始传播者的前提下，比较最终有多少人知晓信息（即属于传播者或沉默者），即图中的纵轴。左图对应大都市模型，右图对应虚拟社区模型。

左图 a 中的不同颜色，代表传播者传播的信息使其他人也变成传播者的概率。在左图中，由于传播导致传播者变成沉默者的概率 λ 为0.1，即使这个消息只要传出去，就会10%的概率让别人也成为传播者。

但由于不同社区之间的流动性太差，最终能够传播到的人群依旧很少。这就解释了为何科普辟谣帖无法触及更多的人。辟谣帖在亲友群中转发后没有人相信，那就相当于在社区之间没有传播。

右图 b 考虑那些本身具有强大说服力、“必转”的信息，这意味着由于信息传播而使未知者变为传播者的概率为 1。但如果信息传播给了一个已经知晓人，这个人可能不再继续传播了，这就是信息饱和。图中不同的颜色代表有不同比例的传播者由于信息饱和而不再传播。但传播者一旦传播给一个已知该消息的人，就停止传播（对应深蓝色的线）。

图中的虚竖线，即信息扩散的临界相变点——在达到相变点之前，即使传播概率（图 a的 p ）和社区内部互动概率（图 b的 μ）在增加，但信息不可能扩散到整个社区。一旦传播概率和社区内部互动概率超过了相变点，信息扩散到整个社区的可能性就会大大增加。

根据上述的传播模型，在一个开放的论坛上，只要在传播的过程中人们有足够的概率和社区外的人建立连接，就有可能使该消息传遍全网。

真实网络中的传播

上述研究都是基于模拟的网络结构，那么在真实网络中是否也存在类似的临界现象呢？超过这一点，消息才有机会传播的更广吗？

论文合著网络是研究者常用的一个数据集。下图展示了在该网络结构中，用蒙特卡罗法模拟信息的传播，左图和右图依旧分别代表了大都市网络模型和虚拟社区模型，横纵轴与上图类似。

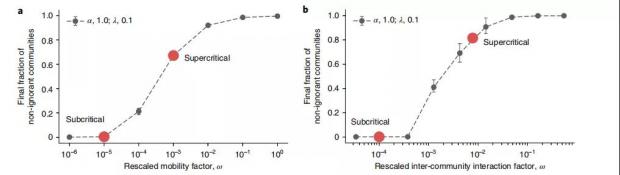
图4：真实网络中信息传播最终效果与社群间流动性关系

从图中可以看出，临界现象依旧存在。研究者进一步分析了在不同状态下，网络中信息传播最终结果，并做了可视化。

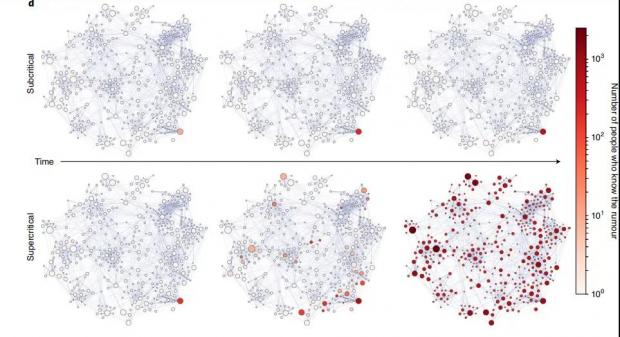
图5：论文合著网络中，到达临界点对信息传播的影响对比

图中的每个点代表一个社区（研究组），点的大小代表该社区的人数，颜色深浅代表该社区中有多少比例的人相信了这则信息。从左到右代表不同时间，上下图对比了处在临界点左右的不同状态。

“10w+”文章的秘密需要进一步研究

这项研究，对于如何做才能让信息在网络得到尽可能广泛的传播，有启示作用。每一则消息因其自身内容的不同，在前文叙述的模型中，会具有不同的 α 或 λ 值，从而使得其在社交网络中传播的范围和速率有所不同。

根据这篇文章的研究来看，相比科普文，爽文之所以能够更容易地获得10w+，是因为爽文能更容易地跨越社群之间的界限，借助人们的共情，传播到不同的社群中。

因此，对于科普文作者来说，如果希望让更多人了解科学知识，就要尊重网络中信息传播的规律。具体而言，即你写的东西要足够简单有趣，才能够跨越社群、而不止在科研圈内部传播，这才是最重要的。其次，要提高传播概率 α ，让你的文章即显得权威又有用（能够帮助读者变得更聪明），实现让更高比例的人传播。

针对本文提出的模型，我们认为有两点值得进一步研究。

首先，原模型中传播者在传播后，只会以一定比例让被传播的人变成传播者，然而在信息的传播中，不是每一个知道信息的人都会愿意转发的。因此可以增加一个参数，表示信息成功传播后，收到信息的人之中有多少比例会变成沉默者，多少比例会变成传播者。该参数代表信息的质量，数值越低则信息的质量越高。加入这个参数后，我们就能够刻画传播能力不同的信息在复杂网络中展现的动力学特征。

第二个改进是在模型中对人群的分类中，加上反驳者这个状态。假设初始的每个社群或区域内，按照特定概率分布，有一定比例的人是反驳者。这些人在接收到谣言时，有一定的概率使传播者变为反驳者。反驳者的加入，能够对谣言与辟谣之间的互动进行研究。

作者：郭瑞东

审校：刘培源

编辑：张希妍

话题：