创新技术如何识别？-集智俱乐部的财新博客-财新网

导语

如何度量技术复杂性？通过将技术建模为组合网络，一篇论文提出了使用结构多样性作为量化技术复杂性的新方法，它基于对复杂网络度量的网络多样性得分改进，可以计算出不同技术网络的复杂性指标，并有效区分复杂技术、中等技术与简单技术。论文结果证明了许多通常与技术复杂性相关的默认事实：如技术复杂性随着时间增长、复杂技术需要更大的研发投入和合作规模、复杂性更高的高新技术往往处在更为集中的空间等等。

法国美术家和作家艾伯特・罗毕达（Albert Robida）在1892 小说《电子化生活》（La Vie electrique）中的插图

技术，这颗来自神话中普罗米修斯为帮助人类而从诸神中骗取的火种，如今已成为人类文明发展的主导力量，如果这不是事实，至少也是默认的共识。自工业革命以来的现代文明，将物质内部力量像欲望一样被解放了，能量与信息纷纷被剥离，并提取、存储与增殖，不再需要魔法，人类从此得以直接利用自然的力量对自然进行控制。

神话消逝，古典陷落，一旦自动机的开关被打开，现代这架巨型机器就开始形成。To be or not to be，人类已没有选择，所能做的，只不过是对它的种种回应，以及，如何回应。

——工具？一种媒介？最强的复制子？抑或在诞生中新的主体？对这些本质倾向的问题，学者们往往众说纷纭，各执一词，最后变成各种概念推演与信念之争。

要解决概念上的种种争端，不如先做，就如科学家们曾对能量、信息、生命、意识所采取的策略一样，先从操作上着手。也就是说，如果我们能找到对技术测量的某几个指标，那么就能从操作性定义的方式来不断逼近它的本质。

这样，我们不仅能借此判断出某项具体技术的价值，还能让国家或企业是否对某些领域进行投入做出的更好决策。

我们真正应该问的问题是：如何对技术进行测量？

论文题目：

Using structural diversity to measure the complexity of technologies

论文地址：

https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0216856

图1：论文作者 Tom Broekel

在 2019 年，发布在 PLoS ONE 上一篇论文《Using structural diversity to measure the complexity of technologies》中，提出了一种量化技术的新方法：通过将技术建模为组件组合网络，可以得出度量技术复杂性的结构多样性指标，即这些网络和子网络中拓扑结构的多样性。这种指标不仅可以有效区分复杂技术、中等复杂技术与简单技术，也被论文证明印证了许多通常与技术复杂性相关的默认事实：如技术复杂性随着时间增长、复杂技术需要更大研发和合作、结构多样性上得分更高的技术也处在更为集中的空间等等。论文作者 Tom Broekel 是挪威 Stavanger 大学商学院教授，也是德国 Bremen大学区域和创新经济学中心的成员，研究方向是区域创新与技术复杂性。

一、复杂性度量：众里寻花千百度引言

二、网络多样性分数：复杂与随机中最美的一个

三、结构多样性指标：技术的源代码

四、量化技术复杂性的实证研究

技术复杂性随着时间增长

复杂技术需要更大的研发投入

复杂技术需要更多合作

复杂技术需要更集中的空间

五、总结：对技术复杂性研究的意义

通过结构复杂性分析技术潜力

考察技术对社会经济的影响

对技术整体趋势量化研究：智能与技术起点

一、复杂性度量：众里寻花千百度

虽然对技术的本体追问难有结果，但大多数学者基本都同意，技术本身是一个层级结构，它来自更低一级技术的组合。对复杂经济学者布莱恩·阿瑟来说，最元初技术是对自然现象及其效应的捕获[1] 。因此将技术视为某种复杂网络，甚至不存在还原过度，真正要解决的只是如何对网络结构进行有效度量。然而，这却是一个很难的问题。

在传统上，可以采用类似统计物理或信息论方法计算某个对象或网络的熵复杂度 [2,3] [4]。例如，在下图中展示了六种典型的网络结构：（a）星形网络（b）晶格网络（c）树形网络（d）小世界网络（e）全连接网络（f）随机网络。

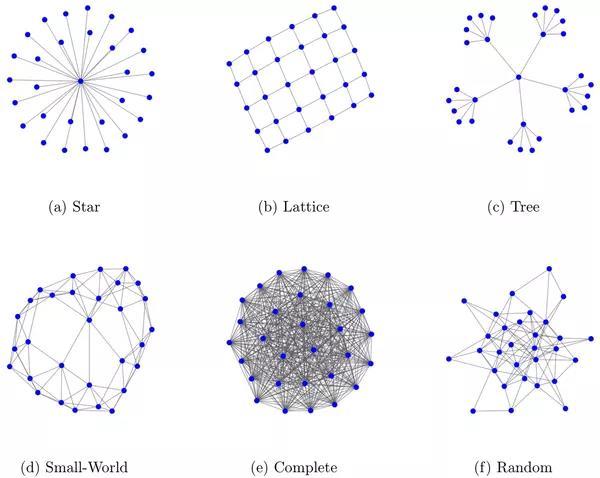
图2：六种典型网络

其中描述星形网络、晶格网络、全连接网络所需要的信息是很少的，它们都属于简单网络，（c）树形网络略微复杂，但也只需要有限信息。最关键的是（d）小世界网络和（f）随机网络之间的对比，尽管小世界网络是典型的复杂网络，但如果按照信息论方法计算，会发现（f）随机网络的所包含的信息量比小世界网络还要高。

因此，对传统的复杂性度量来说，无论是理论上的典型网络,还是诸如生物网络这样的经验网络，最难解决的问题是如何将复杂网络与随机网络、有序网络区分开。即一个有效的复杂性度量分布应该如图2A所示而非B：

图3：复杂性度量有效指标的理论与实际分布

在对实际存在的经验网络研究中，主要基于化学图论（Chemical Graph Theory），即对化学和生物分子结构、以及生态网络的种种性质研究，科学家们曾整理出 16 种网络复杂性度量指标：

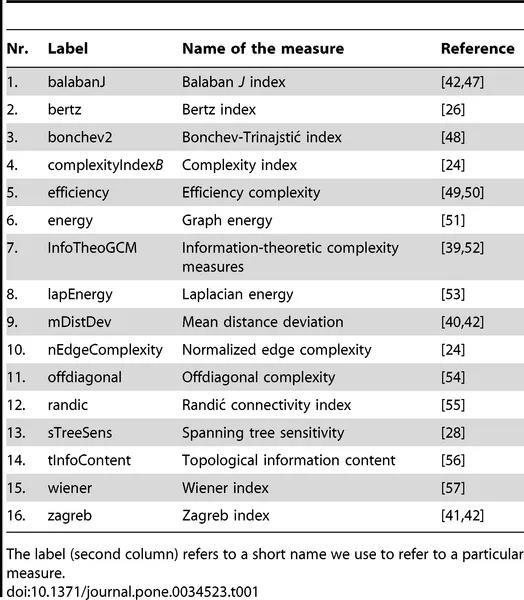
图4：十六种典型复杂网络度度量指标

然而，来自英国和奥地利的两名生物信息学家 Frank Emmert-Streib 和 Matthias Dehmer，在对这 16 种复杂性指标进行验证分析之后 [5]，发现他们几乎都不能有效区分复杂网络与随机网络。

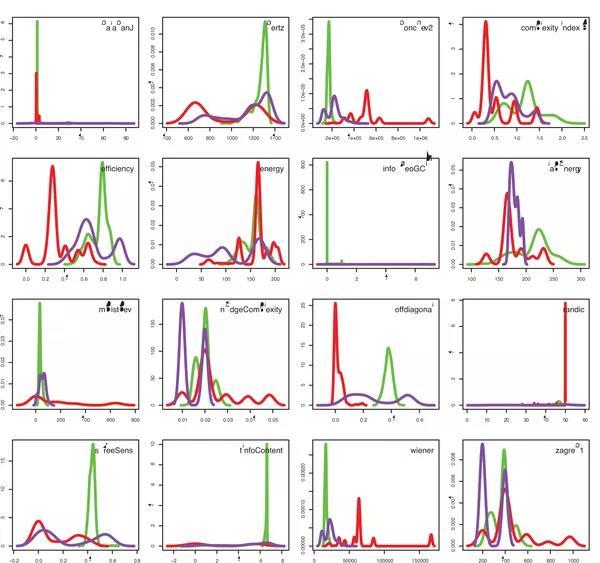
图5：十六种复杂度量指标在数值测试下区分能力表现

结果如图5所示，展示了复杂度值的概率密度（y轴）与复杂度值（x轴）的关系。绝大多数指标都混杂了有序、复杂和随机网络的分布，除了非对角线复杂度能做到基本区分外。但是即使它也有很大问题，不仅有两个分布波峰，而且在复杂网络（紫色）和随机网络（红色）部分也有相当重叠。

二、网络多样性分数：复杂与随机中最美的一个

一个复杂网络可以看做是一个高维对象，仅凭单一维度指标恐怕无法有效解决区分和度量复杂网络，那么综合多维指标呢？

论文题目：

Exploring Statistical and Population Aspects of Network Complexity

论文地址：

https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0034523

沿着这个思路，同样是上面两位生物信息学家在2012 年发表一篇论文:《 Exploring statistical and population aspects of network complexity》，提出了网络多样性指标（Network diversity score，NDS），有效解决了这个问题。他们的方法如下：

设G表示一个网络，该网络具有顶点集V和边集E。顶点的数目为 n=|V|，边的数目为e=|E|。该指标基于以下四个变量计算：

其中 M 是网络 G 中的模块数。向量 m=（m1,m2…）是所包含模块的大小，根据对应该模块节点数大小排列，第i个模块的大小为 mi。为了识别网络中的模块，可以使用一种称为 Walktrap [6] 类似随机游走的方法[7,8]来查找模块，其优点是其能直接估算计算复杂度 O（e*n^2）。

在方程（30）-（33）中的四个变量，分别反映了网络结构中不同属性信息：

变量 αmodule：网络模块密度的信息。模块是网络一般组织原理的基本表达，对复杂网络，人们总希望找到比随机网络更多的模块。

变量 vmodule：类似于CV（coefficient of variation，变异系数）值，测量网络大小相对于模块平均大小的变异性。随机网络的模块大，但可变性较低，平均模块大小也较低，而复杂网络的模块大可变性却较高，模块平均大小也较高。

变量 vλ：与 vmodule 相似，但其参数为拉普拉斯矩阵（Laplace matrix）的特征值[9]。

变量 rmotif：有关网络模体（Network motifs）增长速率信息。从统计中可以观察到，有序网络的 rmotif 值最高，复杂网络居中，随机网络的最低。

在（33）变量中的网络模体（Network motifs），是网络中一种重要的局部特征，它被定义为重复且能被有效统计的子图或模式，可以看做组成复杂网络的基元[14]。最早在生物网络如基因网络中被广泛研究和应用。它与一般的子图区别在于，节点之间角色可能具有不对称性。如图5 a 和 b 所示。

其中 Nmotif（3）和 Nmotif（4）对应于在网络G中发现的大小为3和4的模体数量，图5c同样列出了全部 13 种不同的三节点模体结构。从四节点开始，模体类型总量越来越多，Nmotif（4）总计 199 个，五节点和六节点分别为 9364 和 1,530,843 个。

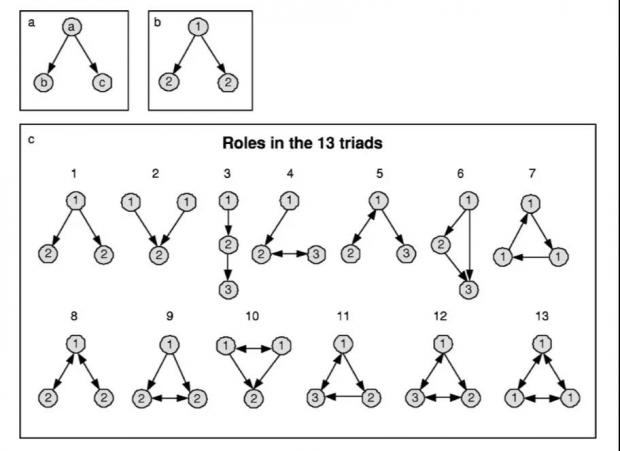
图6：（a）.普通三节点子图（b）.两种节点角色的三节点模体（c）.全部13种三节点网络模体

基于以上四个变量，就可以对网络G定义单个网络的多样性指标（Individual diversity score，iNDS）：

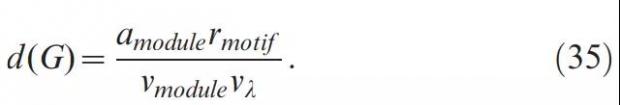
而对包含一个网络集合的 Gm，即有G∈Gm，则整个网络多样性指标为：

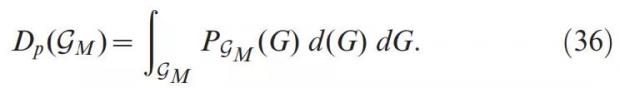
其中，gM表示属于同一网络模型的网络总数，Pgm是该模型总体上的概率分布密度。例如，它可能对应 Erdos-Reyni model [11,12]生成的随机网络，也可以是使用优先附件算法（Preferential attachment algorithm）生成的所有无标度网络的集合[13,14]。

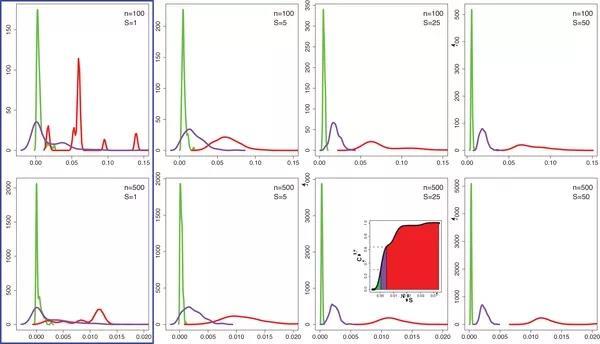
图7：不同样本和节点数下网络多样性指标的效果。样本数 S=50 时三种网络已完全分开

可以看到，网络多样性指标基于多种网络结构原理组合，综合了多种复杂性度量优点进行评估。研究者也论证了在四种变量组合中，通过方程式（35）计算的单个密度数值，能够最佳地分离随机，复杂和有序网络。效果如图6所示，网络节点数和样本总量越大，分离效果越好。当样本 S=5 时，网络多样性指标的效果已经远远超过了十六种复杂性指标中表现最好的非对角线复杂度。

三、结构多样性指标：技术的源代码

如上所述，作为复杂网络度量指标，只有网络多样性分数，能够始终如一地分离有序、复杂和随机的网络结构。

复杂网络代表有序和随机结构的混合体，与有序网络相比，它拓扑异构性更大。但相比之下，具有最大异质性拓扑结构的是随机网络。

在网络多样性指标的研究中，基于科学数值实验生成了大量随机网络，使得网络随机样本化的计算量很大，因此可能忽视了对某些真实网络经验评估的权重。例如在技术网络或知识网络中，与生物网络不同，虽然随机组合形成的网络是存在的，但归根结底，技术发展具有累积特征，其背后的相关社会过程将始终确保系统结构的存在。

因此，为了更有效对技术复杂性进行度量，Tom Broekel 对网络多样性指标进行了修正。由于大小为三和四的模体 rmotif（3）和 rmotif（4）在有序网络中最高，在复杂网络中中等，在随机网络中最低[15] ——然而在网络多样性指标中所有随机网络样本计算数量却很大[16]。

具体方法是针对变量 rmotif 进行了修改，将三和四的模体 rmotif（3）和 rmotif（4）调整为节点数三和四的图的数量 Ngraphlet（3）和 Ngraphlet（4），即符合经验的网络结构之间比值为：

其结果使大值表示随机网络（复杂技术），中值表示复杂网络（中等复杂技术），而低值表示有序网络（简单技术）。

为使用以上使用结构多样性指标，Tom Broekel 使用了经济合作与发展组织（OECD）的REGPAT数据库（2018版），该数据库涵盖了向欧洲专利局提交的专利申请。由于优先权日与专利信息的获取之间存在时间差，分析仅限于1980年至2015年，包括3,137,881项专利申请的信息。技术是根据公司专利网络定义的。公司专利网络分为最高级别的9个类别和最低级别的230,300多个子类别。为了使技术分解和可管理的技术数量之间提供了一个很好的权衡，研究者使用四位数的公司专利网络来定义655种不同的技术进行演技[17,18]。

四、量化技术复杂性的实证研究

对专利的结构多样分析印证了技术复杂性的四个典型事实：技术复杂性随着时间推移而增长，越复杂的技术涉及更多的研发、并且需要更多的协作、复杂的技术倾向于更集中的空间。

技术复杂性随着时间增长

图8显示了1980年至2015年间655项技术结构多样性的分布。

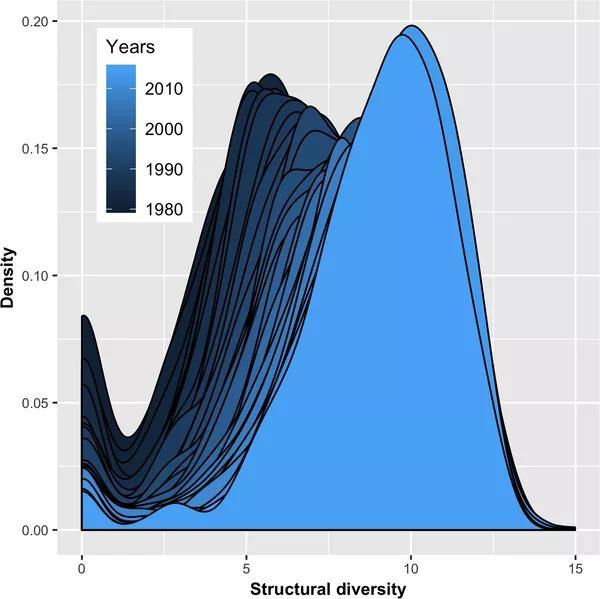
图8：1980 - 2015年，技术结构复杂性分布密度

横轴代表结构多样性复杂度值，可观察最小值为零，最大值为14.98。两者之间纵轴是其概率密度，呈现双峰分布，一个峰值在零点，最大密度峰值在中间。零峰值反映了没有或专利太少、无法计算结构多样性的技术。可以看到，在剔除零处峰值后，无论哪一年，总体都呈现类似正态分布的钟形曲线，只是随着年数增加左边越来越短，右边越来越长，这说明技术复杂性在增大。

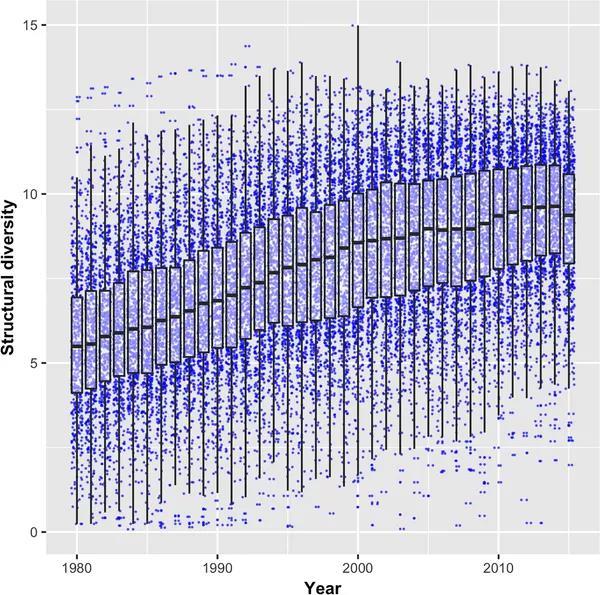
图9：1980 - 2015年，技术结构复杂性中位数箱线变化图

图9 的箱线图直接显示了随着时间增长这些技术的结构多样性中位数变化情况：从 1980 年少于 5，到 2010 年平均已达到 10 左右。这与大多数人印象中技术发展的趋势相符，也证明了技术复杂性在不断增加的观点。

由于知识和技术发展的累积性特征，每一代的新技术都是在前人[19-22] 建立的技术环境基础上发展起来的。随着相邻可能空间扩大，新技术得以可能产生。例如采用数字控制系统的飞机引擎，要比以前液压机械引擎采用更多技术[23]，微软 Windows系统代码从 3.1 的 300 多万增长到 Vista 时已超过 4000 万行[24]。

但值得注意的是，结构多样性的方差仍然很大：不仅2015年的最低值远低于1980年的中值，在1980年代初已达到最大值的技术依然大于最近几年中位数的最高值。也就是说，虽然技术平均复杂性在增长，但每个时代都有自己的复杂技术。技术增长没有想象那么快，从图中可以看到差不多是线性增长。

复杂技术需要更大的研发投入

技术的进步是通过搜索技术空间中潜在的组件，并对技术组合进行测试以创造新的知识组合的，这通常需要反复试验才能完成的[26] [30]。

与简单技术相比，复杂技术基于更大的知识多样性和不太常见的知识组合，这进一步增加了研发的难度。因为学习复杂知识本身就需要更多的资源、更大的吸收能力[27] [31]。复杂技术的这些特征转化为复杂产品就需要更长的开发时间[28] [29]。

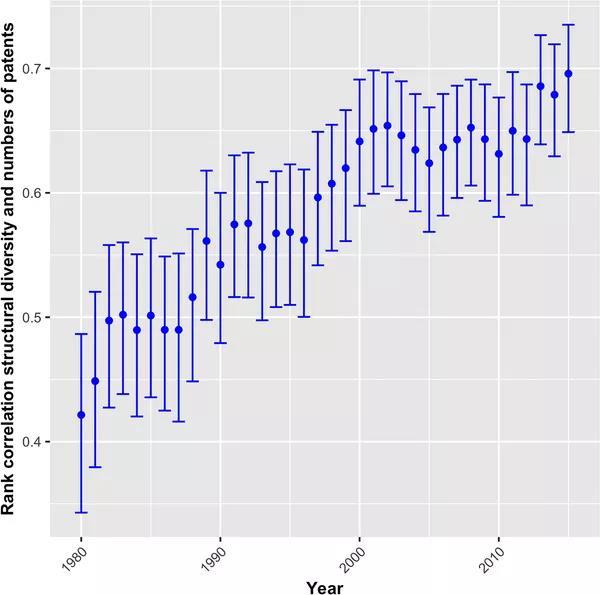
图10：1980 - 2015年，技术复杂性与技术专利数量相关性

图10显示了1980年至2015年技术复杂性与技术专利数量相关性情况。相关系数在所有时间段都非常明显，并且从 r = 0.45 增长到 r = 0.69。就专利数量反映的研发强度而言，结果证实了技术复杂性和研发强度之间的正相关关系。

此外相关系数递增表明，这种关系随着时间的推移而加强——即达到更高的复杂程度比过去更依赖于研发投入。这一潜在趋势地反映了投资回报递减假说：作为研发投入收益随着时间推移递减的结果，创新将越来越多地分布在更多的产品上[32]。

复杂技术需要更多合作

复杂技术通常具有的另一个特征是它们对研发协作的要求更大[33,34,22] [36]，以共同协作解决面临的复杂问题[26]。

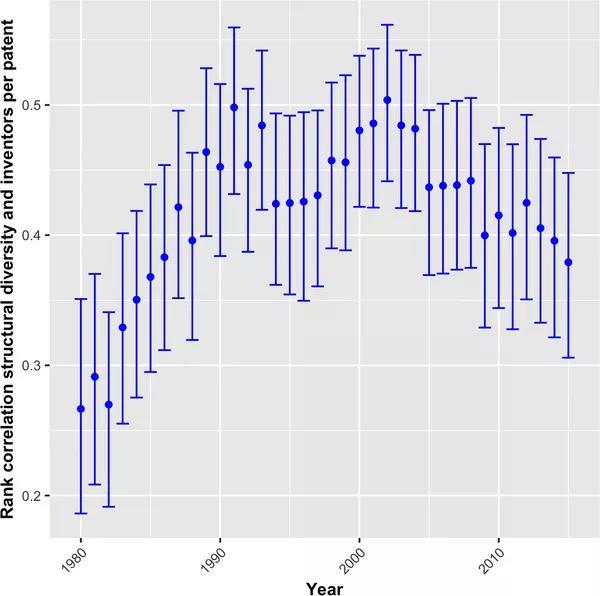
图11：1980 - 2015年，技术结构多样性与专利的平均发明人数相关性

图11显示了技术结构多样性与每项专利的平均发明人数之间的排名相关性，后者表明专利基于团队合作的程度。从这些年看，显著正的相关系数印证了在更复杂技术中进行协作的重要性。在八十年代后期达到约0.4之后，相关系数基本在这个水平浮动。在 2000 年之后相关系数有所下降，可能说明对软件技术，较少的开发人员也可能创造出复杂的技术。

复杂技术需要更集中的空间

在区域经济地理学研究中，通常认为开发复杂技术需要其它地区少有的特殊技能、专业知识、基础设施或研发机构[37-39] [26]。

在学习域区（Learning regions）、创新环境（Innovative milieu）、区域创新系统（Regional innovation systems）[40-42] [35,34]。

为探索结构多样性与技术的空间分布之间的关系，研究结合使用了专利发明人所在地信息，并针对专利数量的技术特定区域分布估算了基尼系数（Gini coefficient），同样针对欧洲 NUTS2 地区，包括 270 个地区和 1,557,416 个项专利。

如果发明人集中在很近几个区域，系数将接近于 1，不然当它们在空间中均匀分布时，该系数收敛为 0。图8显示了技术的空间基尼系数与其结构多样性值之间的相关性。由于专利数量较少的技术在区域间均等分配的可能更小，因此对于至少拥有 1000 项专利的技术，也以红色折现展示了其相关性。

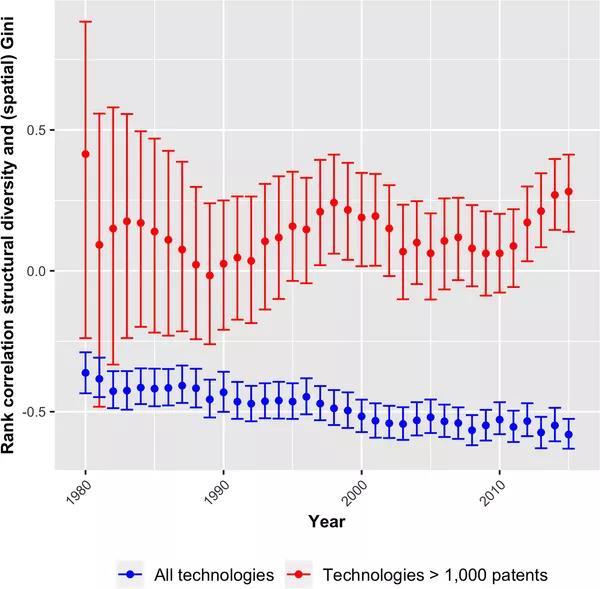
图 12：1980 - 2015年，技术与复杂技术结构多样性与地区基尼系数相关性

当考虑所有技术（蓝色误差线）时，相关性具有强烈的负显着性，表明复杂技术比简单技术分布更均匀。但是，专注于拥有许多专利的技术（红色误差线）时，情况会发生变化。由于拥有 1000 多个专利的技术数量很少，因此相关性在 1990 年代中期之前一直是微不足道的。从那一年开始，相关性在正显着性和不显着之间波动。值得注意的是，自 2009 年以来，该系数一直在增长，并且从 2012 年开始一直保持显着水平，这表明更大、更复杂的技术确实越来越集中的空间中。

五、总结：对技术复杂性研究的意义

一旦找到对技术度量的有效指标，以前让人感到困惑难解或争论不休的那些问题，无论是对某项技术做细节考察，还是对技术整体趋势预测，抑或分析对社会经济的影响，就都有了进一步探讨的依据。

通过结构复杂性分析技术潜力

创新性技术组件间的网络结构，既高度有序，又不会有太多冗余，尤其是新知识和研发投入使得它必然具备了原来没有的节点或结构信息，而非只是无意义的冗余或噪声。

利用结构复杂性和网络多样性指标一个最直接的作用就是，可以准确评估某个技术产品，或者某个网络，是不是具有真正有效的复杂性，还是只是看似复杂的随机网络或人造网络。

例如对 5G 技术，仅凭专利或网络节点数都并不足以说明某一技术方案的优劣。借助网络多样性指标考察其网络的结构复杂性，配合成本分析，在投资或发展某项技术之前，就可能提前预判某种技术方案是否具有足够的创新和发展潜力。

图13：5G承载网络技术总体架构

此外，对网络多样性指标的挖掘可以拓展到任意高维对象，例如对一件艺术品、甚至某个产业生态网络。通过合适的网络建模，可以识别出这些对象究竟是真正具有复杂结构，还是只是通过冗余充数，或借助随机噪声，是让人看不懂的，没有意义的“忽悠”。当然，分析同样适用于生物物种，无论是基因调控网络，还是大脑神经网络。

考察技术对社会经济的影响

复杂技术往往在经济上收益递减，即对高新技术研发，往往具有较低的投入产出比。

在国家层面，有研究指出[21,43]，由于复杂和发展多样性的增加，对高强度研发的投入会超过经济产出、并会因新技能学习困难等因素影响平均收入。这反映在特别复杂的高新技术与所在地区基尼系数的正比关系上（图 11）。

从这点可以理解为什么美国近些年来在削减科研经费，NASA 关闭一些航空项目交给私营航天公司如 SpaceX、Blue Origin 去做。此外在工程中，除了成本外，技术复杂性同样依赖于技术系统的管理[44]。

可见，无论是科研、技术或产品，“低垂的果实”总会很快被采完，高复杂性的创新都需要面临失败的风险和入不敷出的投资回报。

对国家或企业研发而言，最重要是考虑清楚自己所处位置和目标，要实现基本温饱，还是情怀下开拓创造。如果是前者，在发展初期，可以砍掉复杂性过高的技术项目，优先发展中等复杂技术，先发展商业，再搞科技创新。联想总裁柳传志曾提出，先走“贸工技"道路，再走"技工贸”道路，这符合中国早期大多数科技企业的发展路径。

对技术整体趋势量化研究：智能与技术奇点

从图7和图8可以看到，虽然技术随着时间复杂性确实在不断提升，然而却远没有想象中那么快，总体上只是线性比例增长。这个结论与 2020 年 1 月在《Nature Human Behaviour》期刊发表的一篇论文结果类似，该论文对自然和文化演化速率做了定量比较研究。

并且技术也并非总是越在后来越强大复杂，在更早的时候，也有远高于现在技术水平的同类产品，例如阿波罗登月项目，在当时产生了 3000 多项专利，后 1000 多项后来转为民用，总协作人数更是达到了惊人的 30 万人之多，其产生的“土星5号”依然是目前人类历史最强大的火箭推动器（对比 SpaceX 的“猎鹰”[46] ）。

图14：阿波罗登月的“土星5号”与 SpaceX 的“猎鹰”

然而，土星5号的“硬件编程”的操作系统计算能力，却还不如现在一台普通智能手机。

但有趣的是，人们论证技术加速发展的主要依据，却主要来自系统计算能力的提升。如摩尔定律所标示那样，若机器计算能力呈指数级提升，那么几十年后很快会抵达人工智能奇点。这种观点就像是在说一条“快速思维的狗”也会下棋一样。

计算速度只是智能的一个侧面，它并不必然代表系统具有更高的复杂性。

在人工智能领域，以目前主流的机器学习尤其是神经网络技术，也普遍认为目前智能系统瓶颈的突破主要得力于算力的提升和海量数据的采集。

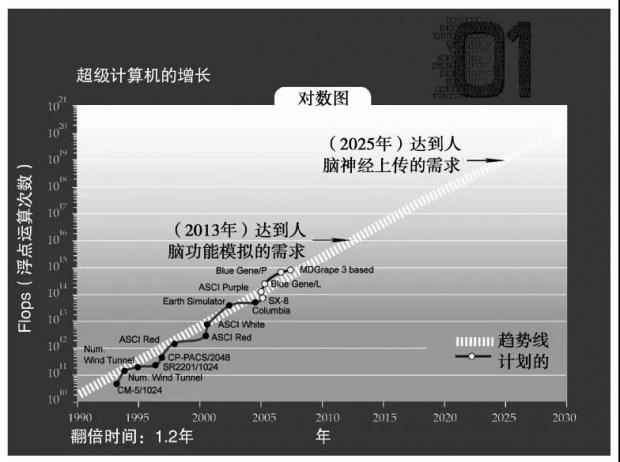
图15：在未来学家 Ray Kurzweil 《奇点临近》中AI超越人类计算能力的趋势时间表

人造技术物的一个最大特征是，能够随着能量和信息的等比例输入而近乎无限地提升系统能力，但本身却不具备更高的复杂性。对不具备更高结构复杂性的 AI 系统来说，其智能水平，虽然有不同机器智能判断标准——通用智能水平，在先天上是存疑的。

如果以生命来对比，那就是生物基因组数量和基因调控网络复杂性。从整体演化树看，从支原体、细菌到鸟类、哺乳动物、两栖动物，生物复杂性是随着基因组大小增长的。（如下图，植物分属不同进化树另论）。显然，基因组数量比较少支原体或细菌，都没有、并不太可能产生类似人类的通用智能。

然而，基因组大小和生物体的复杂性关系只有在原核生物才是线性比例增长。在真核生物中，我们可以看到甲壳动物（Crustaceans）和人类几乎处在同一数量级，并且两栖动物达到 10^10 bp（碱基对数）。这一演化反常曾被称为 C 值悖论（C-VALUE PARADOX）[47]。

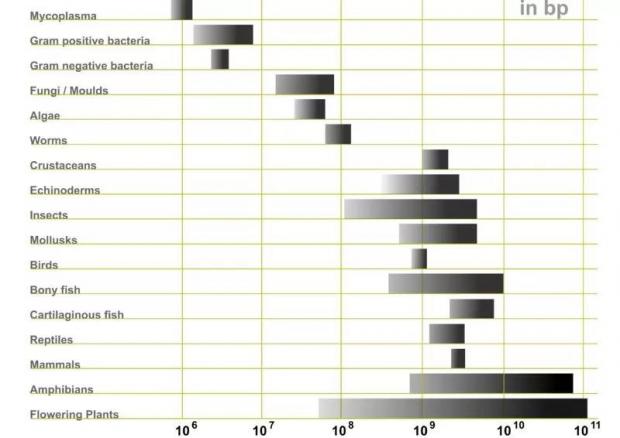
图16：不同种类生物基因组数量对比，单位为碱基对数量

另一方面，今年新研究表明，至少后口动物门（Deuterostomia，包括脊椎动物、哺乳动物）的动物在基因总量上总体一直在“扬弃”：保留新的较少基因突变，丢掉大量无用甚至曾经核心基因[48]。

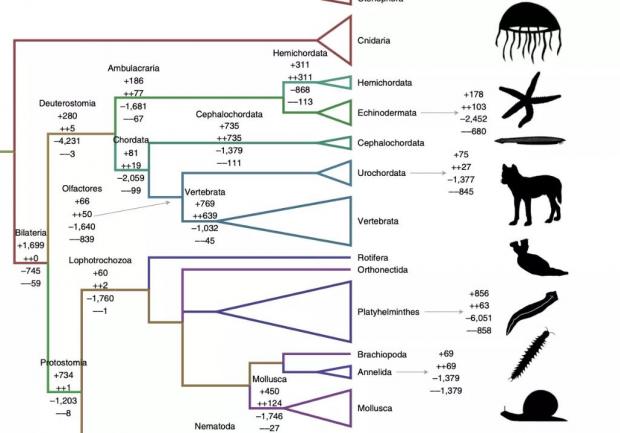
图17：从两侧对称动物（Bilateria）开始，基因增损变化情况

可见，数量不是复杂性的充分条件，只是必要条件。在数量背后，真正起关键作用的是基因调控网络针对环境的调整优化，也即基因功能。越复杂的生物体，越有更多的基因功能，也越适应外部环境。

无论是原生动物绿眼虫简单的眼睛、水螅网状神经系统，或鸟类和哺乳动物发达可塑的中枢神经系统，甚至灵长类可学习能力、语言能力和文化传承能力（例如 FOXP2 对人类语言能力和 MEF2A 对幼儿学习可塑性的重要[49]），都符合这个规律。

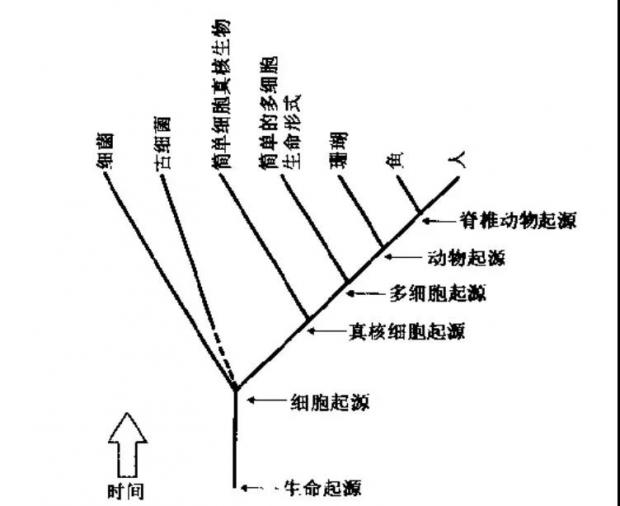
图18：生命复杂性进化的主要事件

这其中一个最典型的例子，就是有性生殖的诞生。Matt Ridley 在《The Cooperative Gene》（中译本《孟德尔妖》）一书中论证，有性生殖为基因组带来了强大的纠错能力，从而提升了生命体所能承载的复杂性上限。此外在理论生物学中也有研究证明，有性生殖能够在增加熵和增加累积适应性之间进行平衡，等价于一种能够在多样性及长期收益之间取得最优权衡的 MWUA 算法[50]。此外，极大提升生物复杂性的还有同源异形基因（Hox genes）[51]等等。

可见，生物体总在自然选择下不断优化自身基因的结构多样性复杂度。简单概括的话，智能系统复杂性 ≈ 自身结构复杂性 + 环境能量输入+ 信息交互复杂性，其中环境和信息部分就是生物适应和改变环境的能力，包括学习能力、协作能力、问题解决和计算能力。在自身达到新的复杂性瓶颈后，人类会利用语言、工具和技术可以说是一种必然。

那么，若从自身结构多样性复杂度和网络多样性指标来看，目前神经网络过于依赖于后天算力和数据，有“多少人工，就有多少智能”，高度依赖和人类的合作。而自身缺乏现实世界的背景知识，和与世界互动的自主能力。因此即使具备超过、能模拟人脑计算能力，也依然只是一个强大的计算设备，很可能就像基因数量达到了10^9 bp 的棘皮动物一样。

因此，图灵奖得主 Judea Pearl 才倡导，人工智能新的突破口在于“因果革命”，让 AI 具备因果归纳和因果推理能力；另一方面，神经形态芯片和类脑芯片硬件研究，机器人的技术的研究，也让人工智能系统在自身结构复杂度上可能进一步大大提升。

目前，结构多样性和网络多样性指标只能让我们计算出一个系统的初始复杂性，但这个问题依然没有解决：即系统自身的复杂性与外部环境究竟怎样交互，才最终怎样决定了一个系统的复杂性与智能水平？

图19：在高加索山上《被缚的普罗米修斯》，美国艺术家 Thomas Cole 于1847年创作的油画

这种其中可能包括环境感知、繁衍方式、多体互动、社会协作、语言文化等诸多问题，虽然暂时没有确切答案，它依然处在一个更复杂的迷雾中，但借助种种量化工具不断进行实践，人类这种智能生物会探索继续下去，总有一天，逼近看清生命和技术的本质——就像古希腊神话中的盗火而被缚的普罗米修斯，他既创造了人类，又是所有知识和技术之父，他的先见之明（Prometheus），终将由人类来解放。

参考文献：

[1] W. B. Arthur, The Nature of Technology: What It Is and How It Evolves (Penguin, London, 2010)

[2] Wiener H. Structural determination of paraffin boiling points. Journal of the American Chemical Society. 1947; 69(1):17–20.

https://doi.org/10.1021/ja01193a005 PMID: 20291038

[3] Shannon CE. A mathematical theory of communication. The Bell System Technical Journal. 1948; 27 (July 1928):379–423.

https://doi.org/10.1002/j.1538-7305.1948.tb01338.x

[4] Dehmer M, Barbarini N, Varmuza K, Graber A. A large scale analysis of information-theoretic network complexity measures using chemical structures. PLoS ONE. 2009; 4(12):20–26.

https://doi.org/10.1371/journal.pone.0008057

[5] Emmert-Streib F, Dehmer M. Exploring statistical and population aspects of network complexity. PLoS ONE. 2012; 7(5). https://doi.org/10.1371/journal.pone.0034523

[6] Pons P, LatapyM (2005) Computing communities in large networks using random walks. In: Yolum p, Gu ¨ngo ¨r T, Gu ¨rgen F, O¨zturan C, editors, Computer and Information Sciences - ISCIS 2005, Springer Berlin/Heidelberg, volume 3733 of Lecture Notes in Computer Science. pp 284–293.

[7] Van Dongen S (2000) Graph clustering by flow simulation. Ph.D. thesis, Centers for mathematics and computer science (CWI), University of Utrecht.

[8] Ziv E, Middendorf M, Wiggins CH (2005) Information-theoretic approach to network modularity. Phys Rev E 71: 046117.

[9] Chung FRK (1997) Spectral Graph Theory. American Mathematical Society.

[10] Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, et al. (2002) Network motifs: simple building blocks of complex networks. Science 298: 824–7.

[11] Erdo ¨s P, Re ´nyi A (1959) On random graphs. I. Publicationes Mathematicae 6: 290–297.

[12] Gilbert EN (1959) Random graphs. Annals of Mathematical Statistics 20: 1141–1144.

[13] Albert R, Barabasi A (2002) Statistical mechanics of complex networks. Rev of Modern Physics 74: 47.

[14] Baraba ´si AL, Albert R (1999) Emergence of scaling in random networks. Science 206: 509–512.

[15] Emmert-Streib F, Dehmer M. Exploring statistical and population aspects of network complexity. PLoS ONE. 2012; 7(5).

https://doi.org/10.1371/journal.pone.0034523

[16] Milo R, Stumpf MP, Stark J, Milo R, Shen-Orr S, Itzkovitz S, et al. Network motifs: Simple building blocks of complex networks. Science. 2002; 298(5594):824–827.

https://doi.org/10.1126/science.298.5594.824 PMID: 12399590

[17] Schmoch U, Laville F, Patel P, Frietsch R. Linking technology areas to industrial sectors. Final Report to the European Commission, DG Research, Karlsruhe, Paris, Brighton. 2003;.

[18] Breschi S, Lenzi C. Net City: How co-invention networks shape inventive productivity in U.S. cities. KITeS Seminarpapers. 2011; p. 1–32.

[19] Nelson RR, Winter SG. The Schumpeterian tradeoff revisited. American Economic Review. 1982; 72 (1):114–132.

[20] Howitt P. Steady endogenous growth with population and R. & D. inputs growing. Journal of Political Economy. 1999; 107(4):715–730. https://doi.org/10.1086/250076

[21] Aunger R. Types of technology. Technological Forecasting and Social Change. 2010; 77(5):762–782.https://doi.org/10.1016/j.techfore.2010.01.008

[22] Hidalgo CA. Why information grows: The evolution of order, from atoms to economies. New York: Basic Books; 2015.

[23] Prencipe A. Breadth and depth of technological capabilities in CoPS: the case of the aircraft engine con- trol system. Research Policy. 2000; 29:895–911. https://doi.org/10.1016/S0048-7333(00)00111-6

[24] Wikipedia. Source lines of code; 2017. Available from: https://en.wikipedia.org/wiki/Source_lines_of_ code.

[25] Fai F, Von Tunzelmann N. Industry-specific competencies and converging technological systems: Evi- dence from patents. Structural Change and Economic Dynamics. 2001; 12(2):141–170.

https://doi.org/ 10.1016/S0954-349X(00)00035-7

[26] Carbonell P, Rodriguez AI. Designing teams for speedy product development: The moderating effect of technological complexity. Journal of Business Research. 2006; 59(2):225–232.

https://doi.org/10.1016/ j.jbusres.2005.08.002

[27] Cohen WM, Levinthal DA. Absorptive capacity: a new perspective on learning and innovation. Adminis- trative Science Quarterly. 1990; 35(1):128–152. https://doi.org/10.2307/2393553

[28] Griffin A. The effect of project and process characteristics on product development cycle Ttme. Journal of Marketing Research. 1997; 34(1):24–35. https://doi.org/10.2307/3152062

[29] Singh K. The impact of technological complexity and interfirm cooperation on business survival. Acad- emy of Management Journal. 1997; 40(2):339–367. https://doi.org/10.5465/256886

[30] Hargadon A. How breakthroughs happen—The surprising truth about how companies innovate. Bos- ton: Harvard Businesss School Press; 2003.

[31] Pintea M, Thompson P. Technological complexity and economic growth. Review of Economic Dynam- ics. 2007; 10(2):276–293.

https://doi.org/10.1016/j.red.2006.12.001

[32] Madsen JB. Are there diminishing returns to R&D? Economics Letters. 2007; 95(2):161–166. https:// doi.org/10.1016/j.econlet.2006.09.009

[33] Hidalgo A, Hausmann R. The building blocks of economic complexity. PNAS. 2009; 106(26):10570–10575.

https://doi.org/10.1073/pnas.0900943106 PMID: 19549871

[34] Balland PA, Rigby D. The geography of complex knowledge. Economic Geography. 2017; 93(1):1–23.

https://doi.org/10.1080/00130095.2016.1205947

[35] Sorenson O. Social networks, informational complexity and industrial geography. In: Fornahl D, Zellner C, Audretsch DB, editors. The role of labour mobility and informal networks for knowledge transfer.Boston: Springer Science+Business Media Inc.; 2005. p. 79–96.

[36] Pavitt K. Technologies, products and organization in the innovating firm: what Adam Smith tells us and Joseph Schumpeter doesn’t. Industrial and Corporate Change. 1998; 7:433–452. https://doi.org/10.1093/icc/7.3.433

[37] Jaffe AB. Characterizing the “technological position” of firms, with application to quantifying technologi- cal opportunity and research spillovers. Research Policy. 1989; 18(2):87–97.

https://doi.org/10.1016/ 0048-7333(89)90007-3

[38] Audretsch DB, Feldman M. R&D spillovers and the geography of innovation and production. American Economic Review. 1996; 86(4):253–273.

[39] Almeida P. Knowledge sourcing by foreign multinationals: Patent citation analysis in the U.S. semicon- ductor industry. Strategic Management Journal. 1996; 17(S2):155–165. https://doi.org/10.1002/smj.4250171113

[40] Florida R. Toward the learning region. Futures. 1995; 27:527–536. https://doi.org/10.1016/0016-3287 (95)00021-N

[41] Camagni R. Local “milieu”, uncertainty and innovation networks: towards a new dynamic theory of eco- nomic space. In: Camagni R, editor. Innovation Networks: Spatial Perspectives. Belhaven Stress. Lon- don, UK and New York, USA; 1991. p. 121–142.

[42] Cooke P. Regional innovation systems: Competitive regulation in the new Europe. GeoForum. 1992; 23:356–382. https://doi.org/10.1016/0016-7185(92)90048-9

[43] Kim BW. Economic growth: Education vs. research. Journal of Global Economics. 2015; 03(04).

[44] Mcnerney J, Farmer JD, Redner S, Trancik JE. Role of design complexity in technology improvement. PNAS. 2011; 108(22):9008–9013.

https://doi.org/10.1073/pnas.1017298108 PMID: 21576499

[45] Ben Lambert, Georgios Kontonatsios, Matthias Mauch, Theodore Kokkoris, Matthew Jockers, Sophia Ananiadou & Armand M. Leroi. The pace of modern culture. 2020. https://www.nature.com/articles/s41562-019-0802-4

[46] David Szondy. Falcon Heavy vs. the classic Saturn V. 2018. https://newatlas.com/falcon-heavy-saturn-v/53090/

[47] Gordon P. Moore, The C-Value Paradox BioScience, Volume 34, Issue 7, 1 August 1984, Pages 425–429. https://doi.org/10.2307/1309631

[48] Cristina Guijarro-Clarke, Peter W. H. Holland & Jordi Paps. Widespread patterns of gene loss in the evolution of the animal kingdom. 4, 519–523(2020). https://www.nature.com /articles/s41559-020-1129-2

[49] Liu X, Somel M, Tang L, Yan Z, Jiang X, Guo S, Yuan Y, He L, Oleksiak A, Zhang Y, Li N, Hu Y, Chen W, Qiu Z, Pääbo S, Khaitovich P. Extension of cortical synaptic development distinguishes humans from chimpanzees and macaques.6. Genome Res. 2012 Apr;22(4):611-22.

[50] Erick Chastain, Adi Livnat, Christos Papadimitriou, Umesh Vazirani，Algorithms, games, and evolution，Proceedings of the National Academy of Sciences Jul 2014, 111 (29) 10620-10623; DOI: 10.1073/pnas.1406556111

[51] CHAPTER 20，Evolution 3rd Edition，MARK RIDLEY，2004

作者：十三维

审校：青子、刘培源

编辑：张爽

话题：